характеризует подъёмную силу, возникающую вследствие разности плотностей.
Критерий Архимеда:
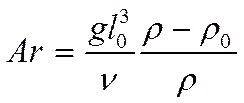 - для двух компонентных сред (вода с
пузырьками).
- для двух компонентных сред (вода с
пузырьками).
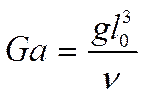 - критерий Галилея.
- критерий Галилея.
Критерий Фруда:
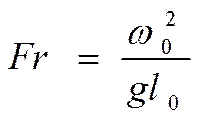
характеризует соотношение сил инерции и сил тяжести.
Использование методов анализа размерности в задачах тепломассообмена.
Представим себе, что мы пытаемся исследовать явление, ранее не изученное. Существует теория размерности. Рекомендации теории размерности: при рассмотрении аналитического описания процессов, ранее не изученного, необходимо:
1) Установить полный перечень существенных для физического процесса размерных величин, которые должны были бы войти в дифференциальные уравнения и условия однозначности.
2) Разделить физические величины на два вида (первичные и вторичные).
3) Установить список ожидаемых безразмерных переменных.
4) Устанавливаем число критериев подобия. Для этого нужна p-теорема (теорема Бэкингема):
Первая формулировка: Число безразмерных комплексов равно числу всех физических разнородных величин существенных для задачи за вычитом числа первичных величин.
Вторая формулировка:
Физическое уравнение, содержащее ![]() размерных величин, из
которых
размерных величин, из
которых ![]() имеют независимую размерность, после
приведения к безразмерному виду будет содержать
имеют независимую размерность, после
приведения к безразмерному виду будет содержать ![]() безразмерных
комплексов (критериев подобия).
безразмерных
комплексов (критериев подобия).
Пример использования p-теоремы.
В
качестве примера рассмотрим пластинку, находящуюся в бесконечном потоке со
скоростью набегания 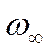 . Вектор скорости направлен по
оси Х, вдоль которой расположена пластина.
. Вектор скорости направлен по
оси Х, вдоль которой расположена пластина.
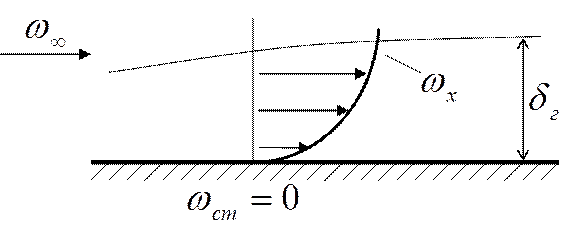 |
|||
 |
|||
Исходя
из методов анализа, найдём связь между координатами. Координата х присутствует
в задаче. Координата у нас интересует в плане толщины слоя, где
развиваются основные события. Эти события связаны с эпюрой скоростей ![]() .
.
![]()
![]()
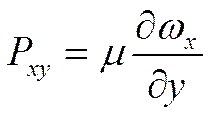 - касательные напряжения.
- касательные напряжения.
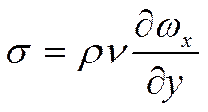
Существенным параметром
является коэффициент ![]() .
.
Посмотрим размерности:
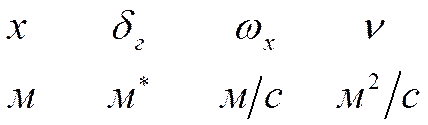
Масштабы
по х и у различаются на порядки. Поэтому у ![]() масштаб иной:
масштаб иной:
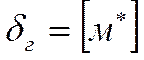 .
.
![]() измеряется в поперечном направлении, то есть
измеряется в поперечном направлении, то есть 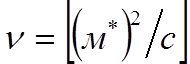 .
.
В теории масштабирования:
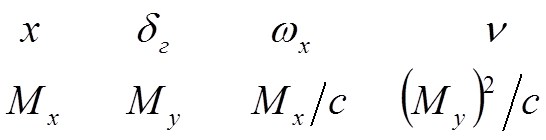
где М – масштаб.
Существенных
величин: ![]()
Независимых
размерностей: ![]() .
.
p-теорема: 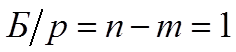 - безразмерный комплекс.
- безразмерный комплекс.
Безразмерный комплекс строим из четырёх величин:
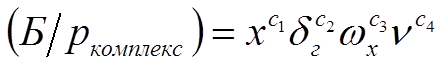
![]()
![]()
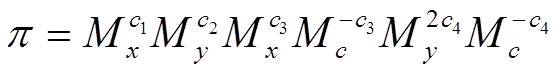
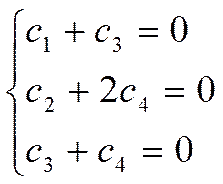 безразмерный
комплекс
безразмерный
комплекс
(в этом случае хорошо выпадет размерность по Х.)
(по У)
(по C)
Это система уравнений для нахождения коэффициентов.
Мы должны найти толщину ![]() . Предположим, что
. Предположим, что ![]() ,
тогда:
,
тогда: 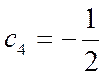 ,
,
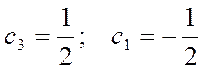 . Мы
получим следующее соотношение:
. Мы
получим следующее соотношение:
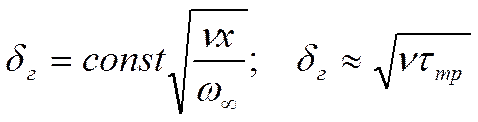
где
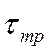 - время транспорта среды
до координаты Х:
- время транспорта среды
до координаты Х: 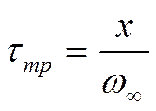

 Введём понятие локального числа Рейнольдса:
Введём понятие локального числа Рейнольдса: ![]() - относится к координате Х.
- относится к координате Х.
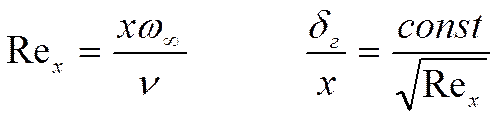
Теорема Гухмана о подобных явлениях.
Подобными процессами будут являться:
1) качественно одинаковые процессы, описываемые одинаковыми дифференциальными уравнениями (в безразмерной форме) и имеющие одинаковую физическую природу.
2) условие однозначности подобных процессов должны быть одинаковыми, кроме численных значений постоянных величин, содержащихся в них.
3) Одноимённые критерии подобия должны иметь одинаковую численную величину.
Система уравнений в приближения пограничного слоя.
Сделаем ряд допущений:
1)
Задачу будем решать стационарную: 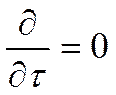
2)
Отсутствуют внутренние источники
тепла: 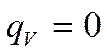
3)
Диссипативными составляющими
пренебрегаем: ![]()
4)
Будем рассматривать плоскую задачу
в плоскости ХУ: 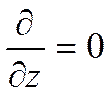
5) Влиянием поля силы тяжести пренебрегаем (вынужденные течения).
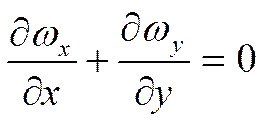 (1) – уравнение неразрывности
(1) – уравнение неразрывности
(2)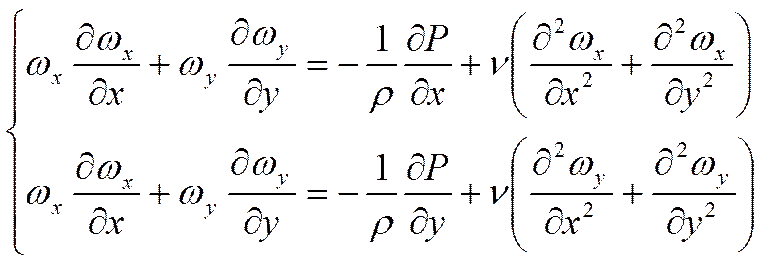
(2) – уравнение сохранения количества движения.
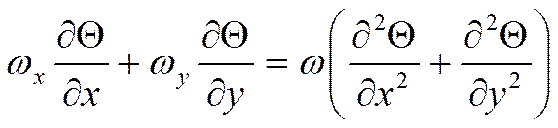 (3) – уравнение энергии.
(3) – уравнение энергии.
Приведём к безразмерному виду:
![]()

![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.