? набегающего
набегающий поток потока
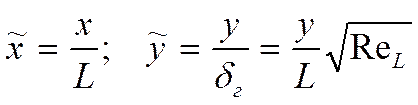
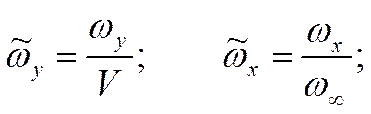
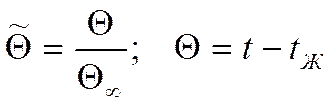
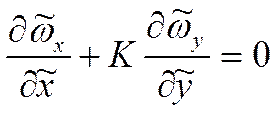
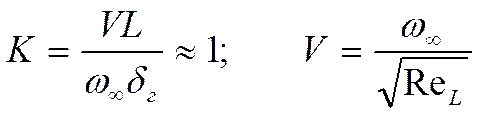
Представим
себе, что мы рассматриваем параметры на значительном удалении от входа, то есть
![]() , тогда:
, тогда:
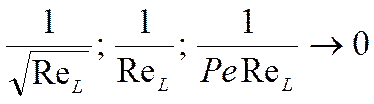
Если составляющими, имеющими такие сомножители пренебречь, получим:
(1) 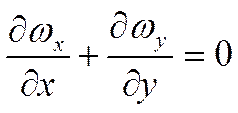
![]() (2)
(2)
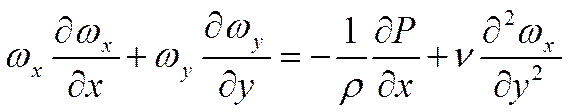
![]() это
уравнение выпадет.
это
уравнение выпадет.
(3) 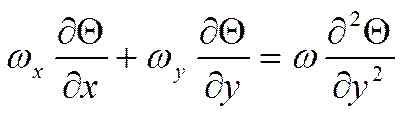
Это уравнения приближений Прандтля – уравнения конвективного теплообмена в приближении пограничного слоя.
Характеристика степени турбулентности потока.
 |
|||
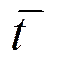

![]() Этот параметр пульсирует в
конкретной точке (параметр самовозмущения)
Этот параметр пульсирует в
конкретной точке (параметр самовозмущения)
 |
|||
 |
|||
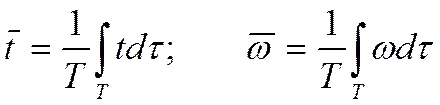
Т – некий
период времени: 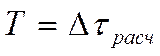
Отклонение температуры и скорости от средних значений называется пульсацией температуры или скорости соответственно.
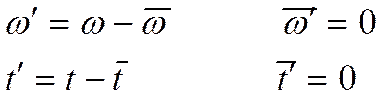
![]() - средний квадрат пульсации скорости.
- средний квадрат пульсации скорости.
Основная характеристика турбулентности:
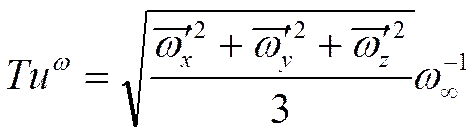
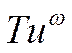 -
по скорости.
-
по скорости. 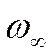 - скорость потока на входе в канал. Чем больше
- скорость потока на входе в канал. Чем больше ![]() ,
тем более развита турбулентность потока.
,
тем более развита турбулентность потока. ![]() - по
температуре (аналогично).
- по
температуре (аналогично).
Расчёт теплоотдачи при продольном обтекании пластины.
Пусть в потоке размещается пластина, температура которой отличается от температуры потока.
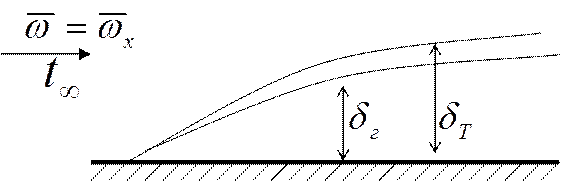 |
|||||||||||||||
 |
|||||||||||||||
 |
|||||||||||||||
Вне зависимости от режима течения потока на входе, формирующийся пограничный слой имеет ламинарный режим течения. Он может перейти в переходный режим, а затем в турбулентный режим. Характеристикой режима течения в пограничном слое является число Рейнольдса.
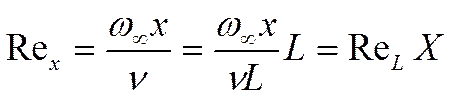
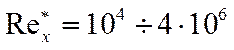 - переходный режим.
- переходный режим.
![]() - ламинарный режим.
- ламинарный режим.
![]() является функцией степени турбулентности набегающего
потока. Чем больше степень турбулентности, тем короче ламинарный режим.
является функцией степени турбулентности набегающего
потока. Чем больше степень турбулентности, тем короче ламинарный режим.
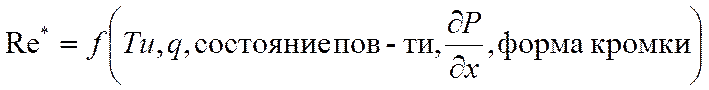
Условно
принято считать, что ![]() близко к
действительности только для обтекаемой входной кромки пластинки. Никогда
ламинарный режим не переходит сразу в турбулентный:
близко к
действительности только для обтекаемой входной кромки пластинки. Никогда
ламинарный режим не переходит сразу в турбулентный:
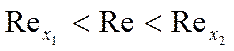
![]() - координата перехода ламинарного режима в переходный;
- координата перехода ламинарного режима в переходный;
![]() - координата перехода переходного режима в турбулентный.
- координата перехода переходного режима в турбулентный.
Рассмотрим ламинарный пограничный слой, где ![]() и будем считать для него справедливыми уравнения
приближения пограничного слоя.
и будем считать для него справедливыми уравнения
приближения пограничного слоя.
Решим сначала , так называемую, гидродинамическую
задачу. Постановка задачи – рассчитать поле скоростей в пограничном слое,
толщину пограничного слоя и коэффициент трения: 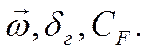
Коэффициент трения – это параметр, равный:
![]()
![]()
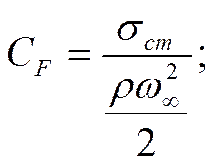
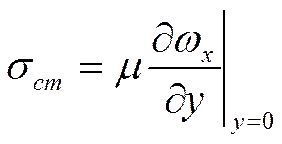 (по
Ньютону)
(по
Ньютону)
![]()
Коэффициент трения входит во все расчеты.
Запишем уравнения пограничного слоя:
(1) 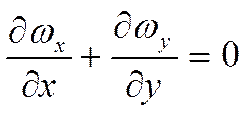
уравнение неразрывности.
(2) 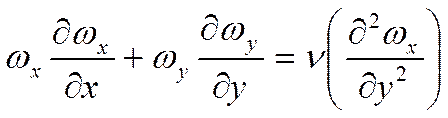
уравнение количества движения.
![]()
![]()
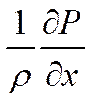 - вследствие приближений тонкой
пластины (Под тонкой пластиной понимается физически тонкое тело вместе с
пограничным слоем, когда ускорением потока можно пренебречь).
- вследствие приближений тонкой
пластины (Под тонкой пластиной понимается физически тонкое тело вместе с
пограничным слоем, когда ускорением потока можно пренебречь).
На границе:
![]() (3)
(3)
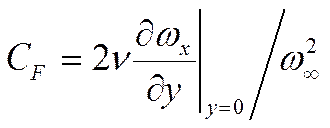
(1)
(2) - математическая постановка задачи.
(3)
Из (1)
следует: 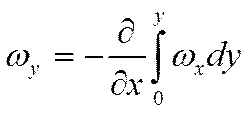
Назовём функцией потока параметр ![]() :
:
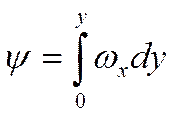
Отсюда ясно, что:
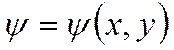
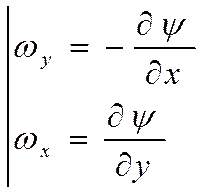
Если это так, то полный дифференциал функции двух переменных выражается следующим образом:
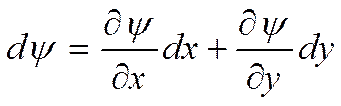
Нам нужны ещё граничные условия:
Если ![]() :
: 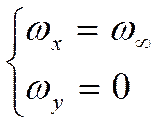
Если ![]() :
: 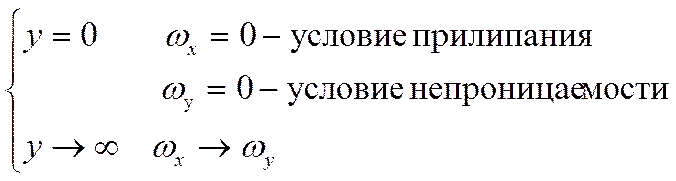
Если 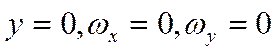 ,
тогда:
,
тогда:
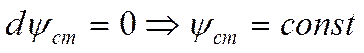
А так как ![]() , то:
, то: ![]() .
.
Введём
“поперечную” координату ![]() , связанную с двумя
координатами у и х соотношением:
, связанную с двумя
координатами у и х соотношением:
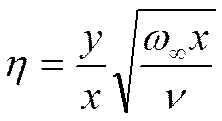
Отметим, что:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.