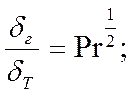Тепломассообмен. Теория тепломассообмена: Курс лекций, страница 22

 если  (характерно для расплавленных металлов).

        (*) – принято для , если режим течения среды ламинарный.

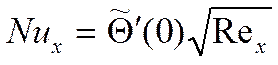
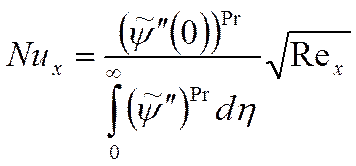
        Если Pr=1, то: 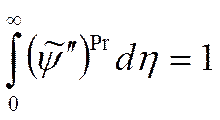  , а значение  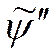мы определили в гидродинамической задаче: .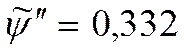

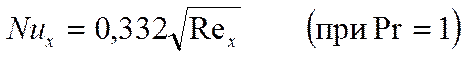
        Обозначим:

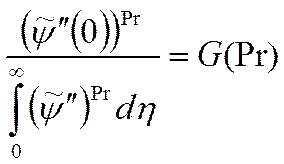
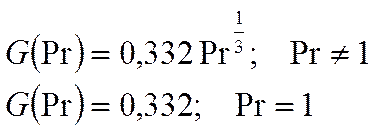
        Итак: 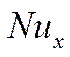- характеризует эффективность теплообмена на пластине.

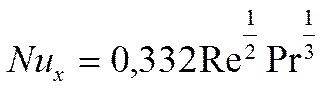
Формула Польгауза.

Формула представляет собой аналитическую зависимость.

Теплообмен при продольном обтекании пластины и турбулентном режиме течения.

Аналогия Рейнольдса.

                                   Эпюра температур                           Эпюра скоростей

 

                                                                                                  Турбулентное ядро

 

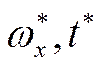                                                                                                               движение                                                                                         

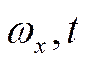
                                                                                                                 массы

 

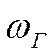                                                                                                             моль

 

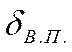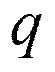обтекаемая кромка

пластины

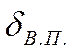 - толщина вязкого подслоя.

        При любом режиме течения среды в пограничном слое вблизи омываемой стенки (пластинки) существует тонкий вязкий подслой. Под вязким подслоем понимается подслой с режимом течения ламинарным. 

Соединим точки пересечения эпюр скоростей и температур с вязким подслоем и обозначим индексом границы подслоя: . Положительное направление потока – это направление от стенки.

         Существует некая плоскость А-А, параллельная нашей пластине. Назовём область невязкого подслоя – турбулентным ядром.

        Обозначим:  - плотность обмена молями

                              - плотность теплового потока, обусловленного обменом молями.

В ядре: 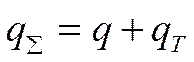      макромеханизм 

                                                                                  переноса

                                       микромеханизм переноса

Гипотеза Фурье: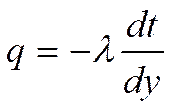  - механизм поперечного обмена теплом.

Гипотеза Ньютона: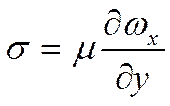   

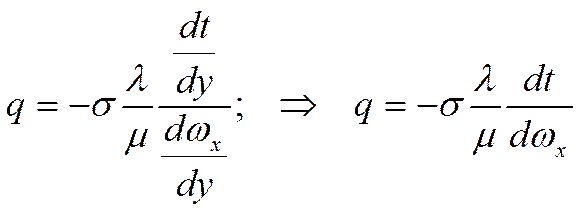
        Молекулярный механизм переноса тепла показывает, что плотность теплового потока пропорциональна касательным (молекулярным) напряжениям. Турбулентный перенос тепла пропорционален турбулентному напряжению. При этом из элементарных макромасс записываем:

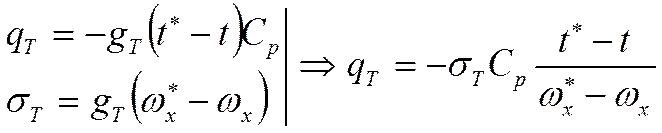
Это математическое отражение аналогии Рейнольдса.

        Из аналогии Рейнольдса следует:

предположим, что в вязком подслое изменение температуры и скорости линейны. То есть в вязком подслое  мы предположили линейность распространения температурного поля и поля скоростей:

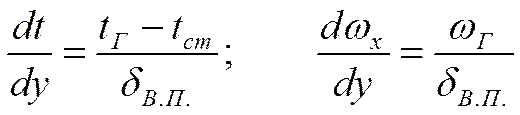
(1)        

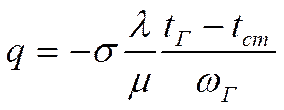
        В зоне  суммарное тепло тождественно определено механизмом молекулярным:

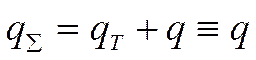
        Параметры , следовательно в любой точке по у тепловой поток . Воспользуемся тем, что нам известны параметры на стенке:

(2)        

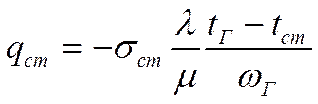
        В турбулентном ядре механизм переноса тепла суммарный:

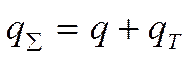
        Предположим, что 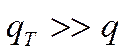(если мы рассматриваем большие числа Рейнольдса). Опытными данными установлено, что это работает, если . Значит:

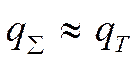
        Рассмотрим границу вязкого подслоя со стороны турбулентного ядра 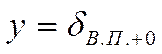 и констатируем факт: ни один из параметров среды не может иметь разрыв своего численного значения на границе вязкого подслоя. Тогда:

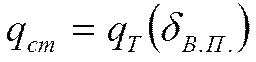 - на границе.

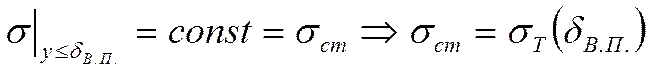
        Допущение: представим себе всю область турбулентного ядра как условную плоскость А-А через которую переносится тепло и количество движения, тогда:

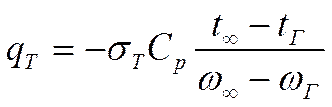   (3)

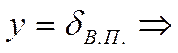
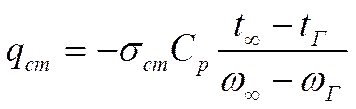Для     (4)

                                                           Рассмотрим совместно уравнения (2) и (4):

Из (2)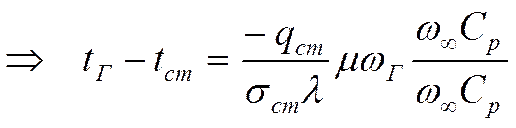  

Из (4)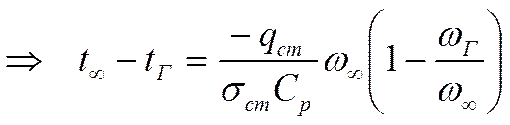  

                                                           Сложим их: