Вся
группа явлений описываемых обобщающим уравнением называется группой подобных
явлений. Физики говорят, что явления этой группы можно рассматривать, как одно
явление, данное в разных масштабах. Математики говорят, что тождество в
относительном математическом представлении есть подобие в абсолютных величинах.
Безразмерные отношения, входящие в описание подобных явлений называются критериями
подобия. Первичные величины – это величины, характеризующие какое либо
явление непосредственно без связи с другими величинами. Первичные величины
могут быть получены прямым измерением и никогда не могут быть получены друг из
друга. Пример первичной величины – время, координата… Любая вторичная величина
определяется косвенным путём по численному значению первичных величин. В любом
дифференциальном уравнении и условиях однозначности к этому уравнению имеются
первичные величины и вторичные величины. Иногда вторичные величины называют
искомыми величинами (например: скорость, температура, давление…). Кроме
разделения на первичные и вторичные величины, принято выделять постоянные
величины: ![]() . Следует обратить внимание, что эти
постоянные величины являются постоянными только для конкретной задачи. Теперь
на примере двух безразмерных комплексов
. Следует обратить внимание, что эти
постоянные величины являются постоянными только для конкретной задачи. Теперь
на примере двух безразмерных комплексов ![]() и
и ![]() мы определим правильную технологию безразмерного
комплекса. Если безразмерный комплекс составлен таким образом, что в него
входит переменная величина, (например время), то такой комплекс называется число
(число Фурье). Если для данной задачи все величины постоянны, то комплекс
называется критерием подобия. const const
мы определим правильную технологию безразмерного
комплекса. Если безразмерный комплекс составлен таким образом, что в него
входит переменная величина, (например время), то такой комплекс называется число
(число Фурье). Если для данной задачи все величины постоянны, то комплекс
называется критерием подобия. const const
![]()
![]()
![]()
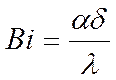 const
const
Введём безразмерные величины:
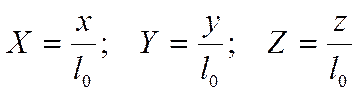
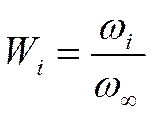
![]() безразмерная
скорость
безразмерная
скорость
![]() на
удалении от стенки
на
удалении от стенки
![]()
Отнормируем: 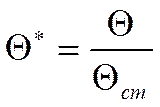
1. Возьмём уравнение неразрывности:
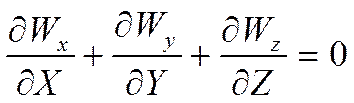
2.
 Уравнение
сохранения количества движения в проекции на ось Х
Уравнение
сохранения количества движения в проекции на ось Х
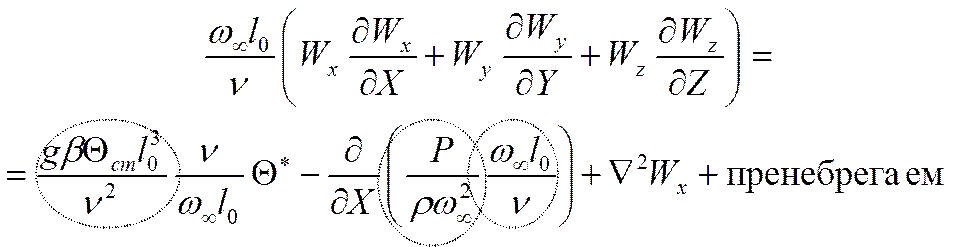
3. Уравнение энергии:

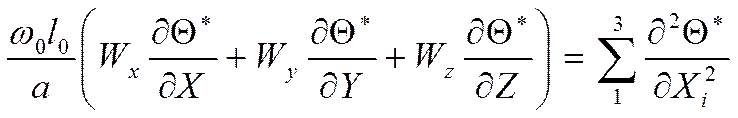
Примечание: кружочком выделены безразмерные величины.
Запишем граничные условия третьего рода:
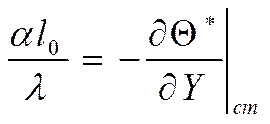
Критерий Нуссельта:
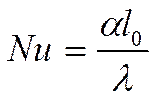
Nu – безразмерный коэффициент теплоотдачи. Физически характеризует интенсивность теплообмена на границе «стенка – жидкость».
Замечание: Нуссельт по виду записывается как БИО, но не имеет никакого отношения к этому числу. Критерий Нуссельта относится только к жидкой среде.
Критерий Пекле:
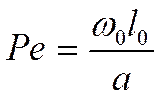
характеризует соотношение количеств тепла, переносимого конвекцией и теплопроводностью.
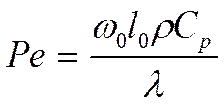
 - константы для задач.
- константы для задач.
Критерий Рейнольдса:
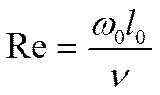
характеризует соотношение сил инерции и сил вязкости.
При малых числах Рейнольдса, выражено преобладание сил трения. Любое возмущение потока локализуется (гасится). Такое течение потока называется ламинарным (от латинского – «полоса»). При больших числах Рейнольдса (Re>2320) течение становится неустойчивым, возникает переходный режим. А при значительно больших значениях Рейнольдса возникает турбулентное течение (от латинского – «возмущающий»), появляются хаотические макропереносы массы и энергии. Механизм переноса массы, энергии и количества тепла при ламинарном течении – молекулярный. (Молекулярный перенос массы – диффузия.) Основной перенос массы, количества тепла и энергии в турбулентном потоке – макромеханизм (молярный).
Критерий Прандтля:
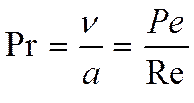
Рассмотрим уравнение количества движения и уравнение энергии:
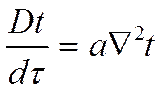
Если рассматривать безнапорное движение, а влияние массовых сил будем считать малым, тогда у нас останется следующее:
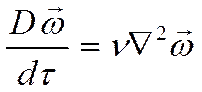
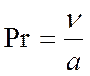 характеризует соответствие поля
скорости и поля температур (или характеризует степень подобия полей скорости и
температур).
характеризует соответствие поля
скорости и поля температур (или характеризует степень подобия полей скорости и
температур).
Если ![]() , то поле скорости и
поле температур подобны для данной задачи.
, то поле скорости и
поле температур подобны для данной задачи.
Критерий Эйлера:
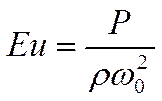
характеризует соотношение сил давления и сил инерции.
Его ещё записывают так: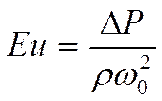
![]() , где
, где ![]() -
давление окружающей среды.
-
давление окружающей среды.
Критерий Грасгофа:
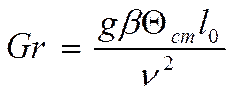
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.