Тепломассообмен. Теория тепломассообмена: Курс лекций, страница 14

 

   Решением является:

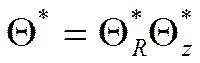
или:

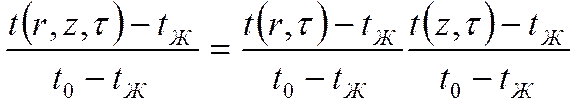
Определение количества тепла, отдаваемого телами при охлаждении.

     Постановка задачи: определить количество тепла отдаваемого в окружающую среду телом, охлаждённым с первоначально постоянной температуры  до заданной  (средняя температура).

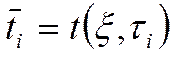
Полное количество тепла запасённого в теле по определению:

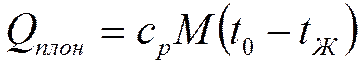
- масса тела

     Если мы имеем тело, которое можно считать бесконечным, то количество тепла определяется с единицы поверхности.

Для бесконечной пластины:    

Для бесконечного цилиндра: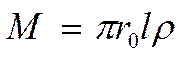   

 

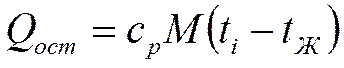
Тепло, оставшееся после охлаждения до 

Отданное окружающей среде тепло:

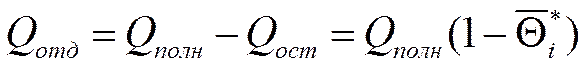
Где: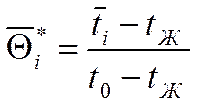      

     Если мы осредним эту функцию по времени, мы получаем решение задачи.

1)  Бесконечная пластина:

 

                                                  

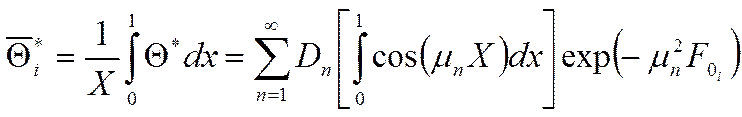
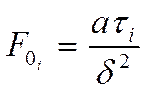
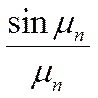
   Рассмотрим частные варианты вырождений чисел БИО:

1) 

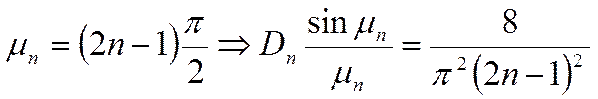
2)                                   

                            

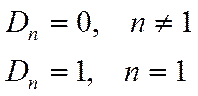
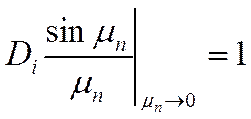
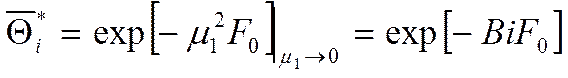
2)  Бесконечный цилиндр:

Важно найти среднюю температуру в данный момент времени.

 

Смотри справочные данные. Поиск сводится к средней температуре.

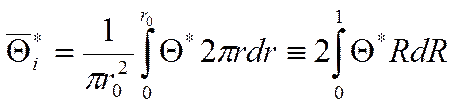
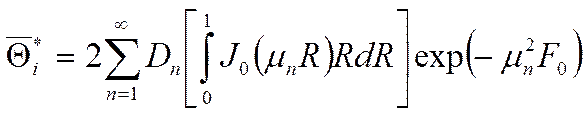
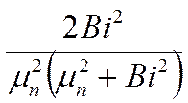
Регулярный режим охлаждения (нагревания) тел.

Бесконечная пластина.

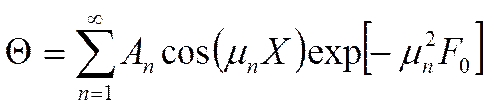
- физические свойства и начальные условия.

- физические условия и координаты.

        Вернёмся к первоначальной записи :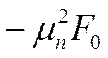

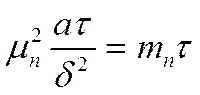,   где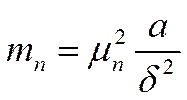

 

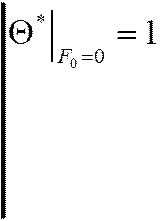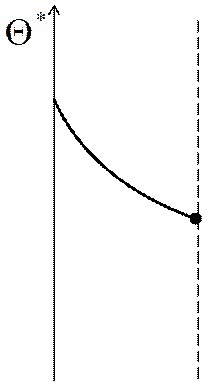
При малых временах реальное температурное поле – есть неупорядоченная стадия. Есть слои, которые ещё «не знают» об охлаждении среды.

   Пусть  соответствует . Изменение температурного поля будет зависеть от физических свойств тела и от координат.

 

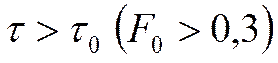 1                                                       

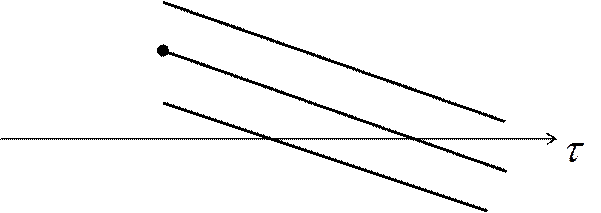       неупоряд.

          стадия

     охлаждения

             Если 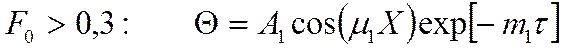, то работая в логарифмических координатах, получим следующее:

          (*)

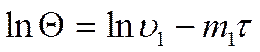где .         Угол наклона определяется 

        Эта стадия охлаждения или нагревания  когда описывается одним членом ряда называется регулярным режим охлаждения, нагревания тел.

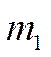
Продифференцируем функцию (*):

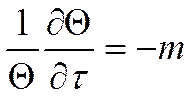
          Параметр равный от 1 до  называется темпом охлаждения или нагревания тела.

          Темп охлаждения можно определить экспериментально. Найдя и выбрав  :

 

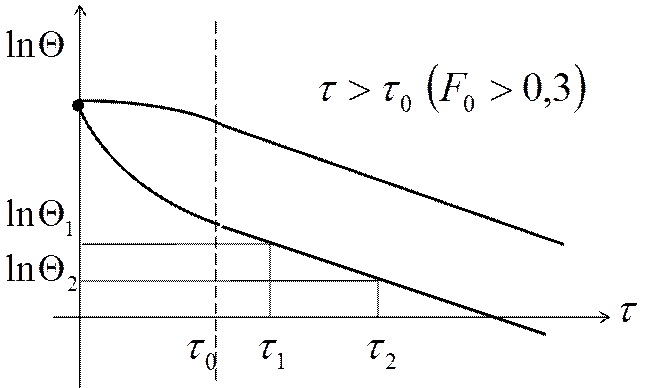
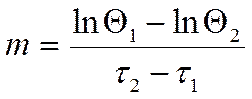
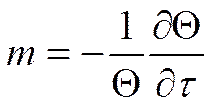
          В регулярном режиме темп охлаждения не зависит от координат и времени и является постоянной величиной для всех точек тела.

Теоремы Кондратьева для регулярного режима.

1)  Темп охлаждения пропорционален коэффициенту теплоотдачи и обратно пропорционален полной теплоёмкости тела.

Доказательство:

          Обозначения:  -количество тепла [Дж],

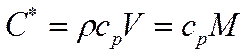 - полная теплоёмкость тела.

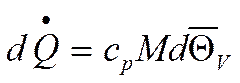   где: 

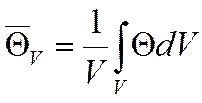
Согласно Ньютону-Рихману за время проходит количество тепла:

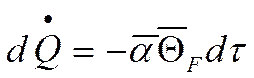
если ;    знак минус показывает, что тепло удаляется.

    перепишем:

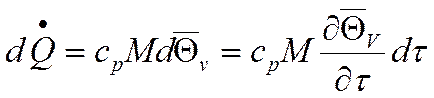
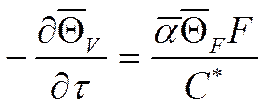      Домножим на :

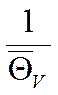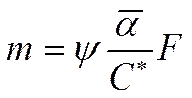
где: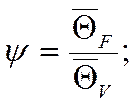         

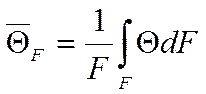
          Теорема доказана.

2)  При числе темп охлаждения пропорционален коэффициенту температуропроводности.

Пластина:

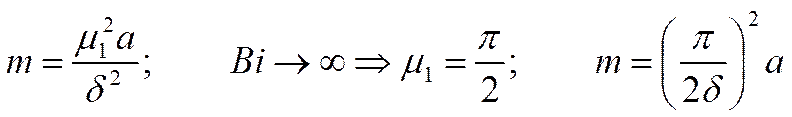
Цилиндр:

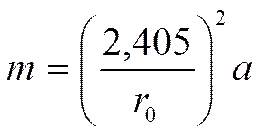
Обычно в учебниках: , где k - коэффициент формы тела.

    для пластины: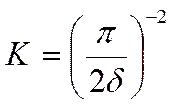 

    для цилиндра: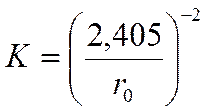 

    для шара: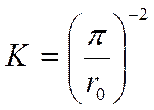 

    цилиндр конечной длинны: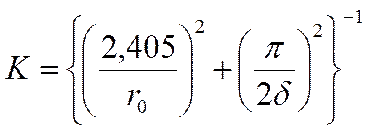 

    параллелепипед: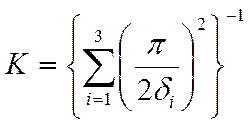

Конвективный теплообмен.

     Совокупность процессов конвекции и теплопроводности называется конвективным теплообменом.

     Если рассматривается конвективный теплообмен на границе: текучая среда – стенка, то такой процесс называется теплоотдачей.

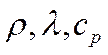         - вязкость?

             - коэффициент температурного расширения среды.

     Впервые коэффициент вязкости ввёл Ньютон.

Рассмотрим твёрдую стенку и вектор скорости, направленный по оси Х:

 

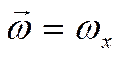
    y