Для ребра произвольного сечения:
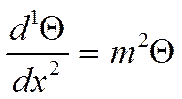
 Его решением является:
Его решением является:
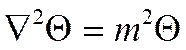
Перепишем это решение для круглого ребра в
цилиндрической системе координат, учитывая, что задача одномерная. Если ребро
тонкое и ![]() и
и 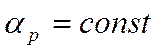 , то
задача одномерная.
, то
задача одномерная.
Итак, если![]() , то
, то ![]() записывается:
записывается:

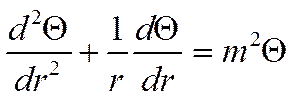
Обозначим: ![]()

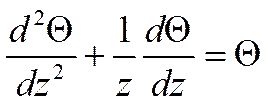
Уравнение Бесселя
Решением этого уравнения всегда являются две функции:
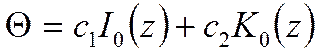
![]() - модифицированная функция Бесселя первого
рода нулевого порядка.
- модифицированная функция Бесселя первого
рода нулевого порядка.
![]() - модифицированная функция Бесселя второго
рода нулевого порядка.
- модифицированная функция Бесселя второго
рода нулевого порядка.
 При
При ![]()
При
![]()
Существуют таблицы, в которых можно найти соответствующие значения функций.
![]() и
и ![]() находятся из граничных условий.
находятся из граничных условий.
Граничные условия: 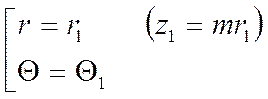
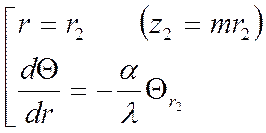 (гр.
усл. IIIр.)
(гр.
усл. IIIр.)
Решением будет функция некоторых параметров:
![]()
![]()
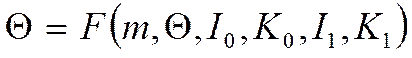
По существу нам надо от круглого ребра, а не .
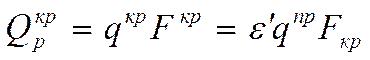
где
![]() - поправочный коэффициент, который
характеризует отличие тепловых потоков:
- поправочный коэффициент, который
характеризует отличие тепловых потоков:
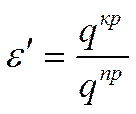
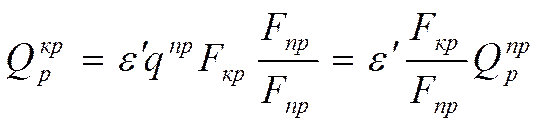
Рассчитывать 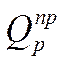 мы уже умеем.
мы уже умеем. 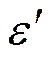 - зависит от геометрии прямоугольного ребра.
- зависит от геометрии прямоугольного ребра.
При расчёте 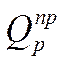 принимается следующая его геометрия:
принимается следующая его геометрия:
![]() такое же как у круглого,
такое же как у круглого, ![]() ,
, 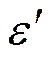 - в справочниках, величина
- в справочниках, величина ![]() взаимно уничтожается.
взаимно уничтожается.
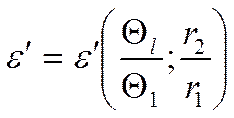 - функция двух отношений.
- функция двух отношений.
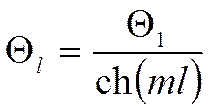
Нестационарные процессы теплопроводности.
Запишем решение нестационарных задач в декартовых координатах.

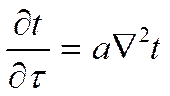
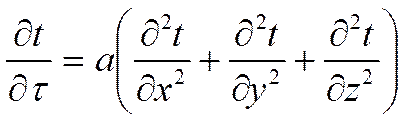
Начальные условия ![]() должны быть заданы.
должны быть заданы.
Граничное условие задаётся в виде граничных условий III рода:
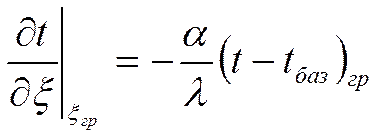
![]() - любая
координата (x,y,z).
- любая
координата (x,y,z).
Кроме того, мы должны знать
внешние параметры, то есть размеры 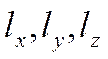
и теплофизические параметры: 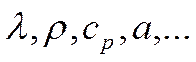
Незнание одного из условий переводит задачу в нерешаемую.
 |
|||||
Поместим болванку в печь
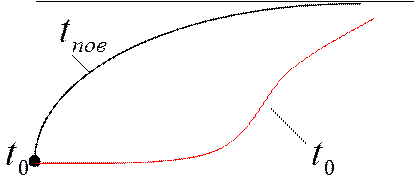 |
- температура на оси или центральной пл-ти
Изменение температур в разных точках тела будет разным. На поверхности температура будет расти сразу, внутри – через некоторое время (время запаздывания). Имеет место разность температур в разных точках тела.
Охлаждение (нагревание) бесконечной пластины.
Задача решается одинаково и для нагрева и для охлаждения.
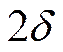
![]()
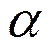
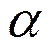
![]()
![]()
![]()
![]() Будем
считать, что пластина бесконечна постоянной толщины
Будем
считать, что пластина бесконечна постоянной толщины ![]() .
.
![]() Разместим начало координат в серединной плоскости.
Разместим начало координат в серединной плоскости.
![]()
![]()
Постоянное поле температур в начальный момент времени.
Известно:
![]()
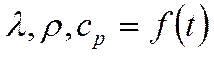
![]()
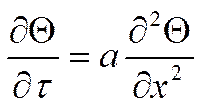 Задача одномерная,
пусть
Задача одномерная,
пусть 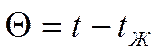
- уравнение теплопроводности
для нестационарной задачи.
Зададим ряд постоянных начальных условий:
![]()
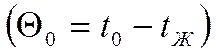
Два граничных условия:
1)
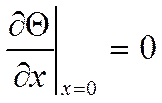 -
условие симметрии. Температуры в симметричных точках относительно оси z
равны. Будем решать задачу от 0 до
-
условие симметрии. Температуры в симметричных точках относительно оси z
равны. Будем решать задачу от 0 до ![]() .
.
2) Граничные условия III рода:

Используем метод разделения переменных.
Предположим, что решение может быть представлено как произведение двух функций: одна функция зависит от времени, другая – от координат.
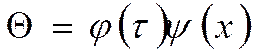
Ищем решение:
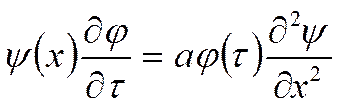
Пусть: 
![]()
![]()
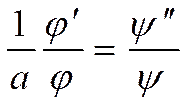 (*)
(*)
![]()
![]()
Эти функции могут быть равны, только если (*) = const.
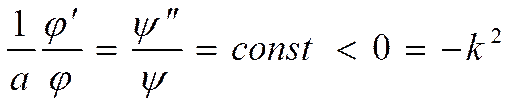
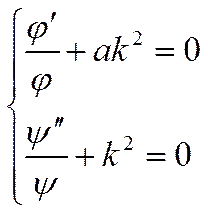 |
Решение первого уравнения: 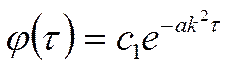
Решение
второго уравнения: 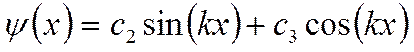
Воспользуемся условием симметрии:
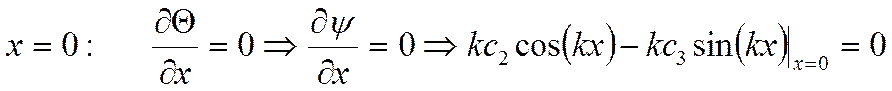
Отсюда ![]()
Итак: 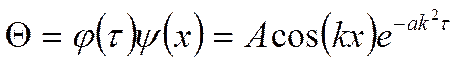 , где:
, где: ![]() .
.
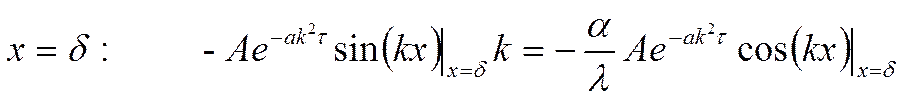
![]() Сгруппируем:
Сгруппируем: 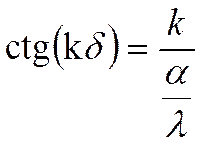 умножим на .
умножим на .
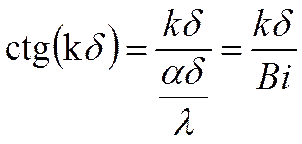
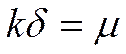

Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.