Лабораторний практикум з дослідження цифрових пристроїв на основі САПР MAX+PLUS II, страница 68

Методику проектування розглянемо на прикладі побудови паралельного лічильника з модулем М = 5 і природним порядком лічби, який має перемикатися за часовими діаграмами (рис. 8.8).

1) За потрібною кількістю розрядів n = 3 аналогічно табл. 8.1, 8.2 у перемикальній таблиці (рис. 8.9, а) заповнюємо колонки початкового Q_і та наступного по надходженні лічильного імпульсуQ_і⁺ станів тригерів з урахуванням того, що коди N = 5 ... 7 є надлишковими.

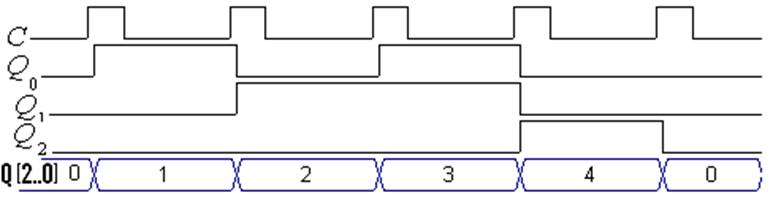
Рисунок 8.8

2) Вибираємо тип тригерів (для прикладу розглянемо варіанти лічильника на JK-, D- i TE-тригерах) та заповнюємо стовпці таблиці для функцій збудження на їхніх інформаційних входах. Так, у JK-тригеру старшого розряду колонкам Q₂Q₂⁺ лівої частини таблиці відповідають колонки J₂K₂ її правої частини. Тому для переходівQ₂Q₂⁺ = 00, 01, 10 вносимо значення J₂K₂ = 0Х, 1Х, Х1, відтак аналогічно заповнюємо колонки для всіх інших розрядів згідно з таблицею переходів JK-тригера. Для розрядів на D-три- герах вносимо значення D_і = Q_і⁺, а на ТЕ-тригерах записуємо Е_і = 0, якщо тригер не перемикається та Е_і = 1, якщо перемикається.

3) Безпосередньо з таблиці довизначенням Х = 1 маємо К₂ = К₀ = 1, а інші функції збудження мінімізуємо за діаграмами термів (на рис. 8.11, б) порожнім клітинкам відповідають факультативні значення Х):

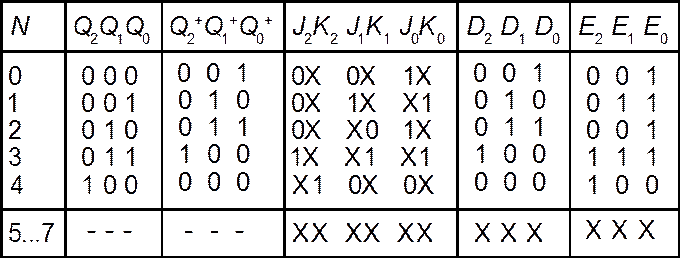
а)

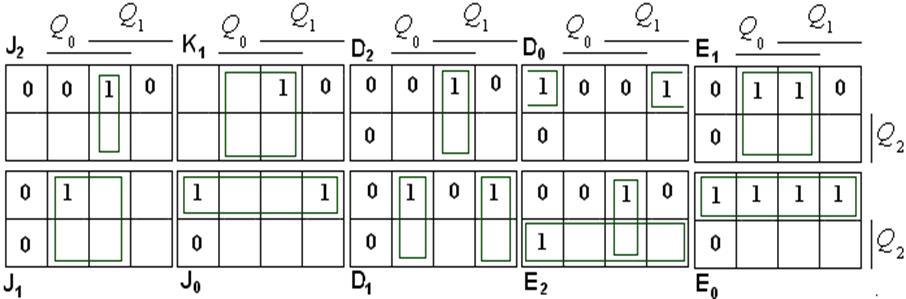
б)

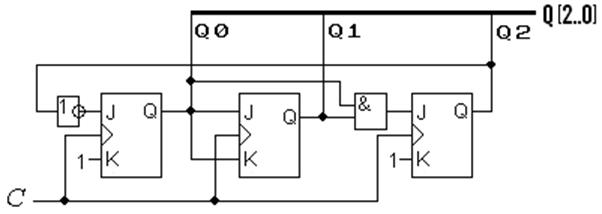
в)

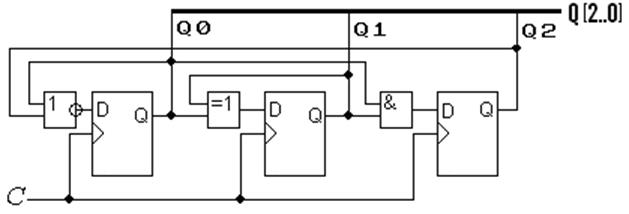
г)

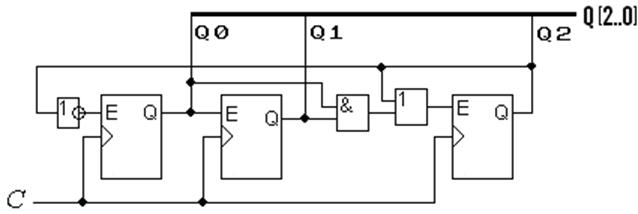
д)

Рисунок 8.9

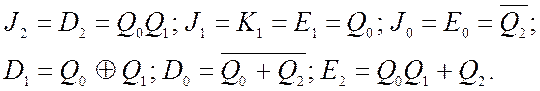
4) З’єднуючи синхровходи тригерів зі спільним лічильним входом С, а інші входи – згідно з функціями збудження, отримуємо варіанти реалізації лічильника на JK-, D- i TE-тригерах (рис. 8.9, в), г), д) відповідно). Такі лічильники є синхронними, отже, перемикаються без проміжних станів вихідного коду (див. рис. 8.10).

Найпростіший щодо реалізації варіант визначається елементною базою. Так, лічильники на JK-тригерах з дубльованими входами потребують мінімуму додаткових елементів у міжрозрядних зв’язках (при викори- станні інверсного виходу і подвійних входів у старшому розряді схема на рис. 8.9, в) не містить таких елементів) і можуть виявитися зручними для побудови на ІС жорсткої структури.

На програмованих ІС економічнішими є схеми на D- і RSC-тригерах з динамічним керуванням. Крім того, для низки застосувань доцільною є побудова лічильників з довільним модулем і порядком лічби за схемами з послідовним і комбінованим перенесенням.  

8.1.3.3 Макрофункції і універсальна мегафункція

Серед ІС лічильників приблизно половина є декадними, з модулем лічби М = 10 (символи 1...7 на рис. 8.10), послідовним з’єднанням яких можна отримати лічильник з модулем М = 10ⁿ. Такі лічильники є паралельними за схемою зі зворотними зв’язками і задля гнучкості використання можуть містити в корпусі ІС окремі лічильники з модулем М = 2 і з модулем М = 5 (див. рис. 8.9, г), послідовне з’єднання яких утворює асинхронний лічильник з модулем М = 10 (символи 1, 3, 4). Наявність в корпусі ІС ще й декадного лічильника (символ 1) дає змогу отримати також модулі М = 20, 50, 100.

Користуючись входами скидання до нуля CLR(символи 1...4), передустановлення до дев’ятого стану SET9 (символи 2, 3) та завантаження сигналом LDNзі входів A, B, C, D(символ 4), декадні лічильники, як і двійкові, можна перетворити у недвійкові з довільним модулем шляхом примусового скидання або нараховування.

Реверсивні декадні лічильники будуються за таким самим принципом, як і двійкові: з одним лічильним входом U/DN (символи 5, 7) або з двома – додавання UP та віднімання DN (символ 6). Засвоєно випуск низки лічильників з додатковими функціями, наприклад, з вихідним регістром і трьома станами виходу (символ 7) або з дешифратором семисегментного коду (символ 9). Є також спеціалізована щодо програмного пакету макрофункція для лічби в коді Ґрея (символ 8).

Універсальна мегафункція (символ 10) дозволяє реалізувати потрібний тип двійковокодованого лічильника з довільним модулем лічби.