Лабораторний практикум з дослідження цифрових пристроїв на основі САПР MAX+PLUS II, страница 15

Рисунок 2.1 – Мінімізація логічної функції y чотирьох змінних

Інверсну функцію МДНФ також можна отримати з цієї самої діаграми, зчитуючи сполучення нулів так само, як сполучення одиниць:

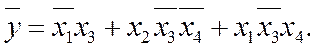
2.1.2  Реалізація в поширених базисах

Булів базис – функції реалізуються сполученням входів і виходів логічних елементів у послідовності: НЕ, І, АБО відповідно до формул у МДНФ або в послідовності: НЕ, АБО, І за формулами в МКНФ.

Базис І-НЕ – після мінімізації логічної функції в МДНФ (об’єднанням одиниць)  реалізацію звичайно виконують за формулою:

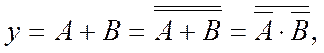                                                     (2.1)

де  А, В – кон’юнкції літералів  (змінних  або їх заперечень).

Базис АБО-НЕ –після мінімізації логічної функції в МДНФ (об’єднанням нулів) реалізацію звичайно виконують за формулою:

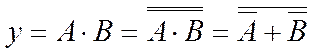                                         ,            (2.2)

де А, В – диз’юнкції літералів.

Базис І-АБО-НЕ – після мінімізації інверсної логічної функції в МДНФ (об’єднанням нулів) перетворення схем виконують алгебрично за формулами:

                                        ,         (2.3)

де А, В – кон’юнкції літералів.

2.1.3  Способи спрощення логічних схем

Серії сучасних ІС містять різні комплекти стандартних логічних елементів, у тому числі багатовходових, використання яких дозволяє мінімізувати схеми.

Редукцію в диз'юнктивній формі в загальному вигляді під час мінімізації в ДНФ можна виконати доповненням заданої функції у неперетинною з нею коригувальною функцією у_k таким чином, аби об'єднання D цих функцій та сама допоміжна функція у_k були якомога простішими. Тоді шукану функцію дістаємо з виразу

                                                  .                    (2.4)

Редукція в кон'юнктивній формі – до нульових клітинок функції у з метою спрощення їх сполучень на діаграмі долучаємо ще деякі одиничні клітинки, утворюючи допоміжну функцію у_k, якщо доповнення об'єднання  цих функцій (тобто сполучення нульових і ще приєднаних одиничних клітинок) і нова функція у_k виявляються простими. Для здобуття шуканої функції необхідно в утвореному об'єднанні відновити одиничні клітинки, тобто виконати операцію імплікації

                                                                                         (2.5)

Алгебричне виконання редукції  у простих випадках можна здійснити за формулами:

                                   (2.6)

Приклади та інші відомості щодо мінімізації логічних функцій, реалізації їх у поширених базисах і схемної мінімізації наведено в [1, 2].

2.1.4 Макрофункції

Макрофункція(Мacrofunction) – стандартний блок, здебільшого високого рівня, з оптимізованими різноманітними логічними операціями. У системі МАХ... запроваджено понад 300 макрофункцій на базі 74-ої серії (з цифровою нумерацією 74...), а також специфічних для цієї програми (позначаються маленькими літерами). Макрофункції можуть використовуватися в графічних і текстових файлах разом із примітивами та іншими структурними компонентами. З використанням макрофункцій зручно відпрацьовувати проекти, що будуються на ІС жорсткої структури.

Макрофункції зосереджено в підкаталозі \maxplus2\max2lib\mf бібліотеки функціональних модулів САПР. Для добору потрібної макрофункції найзручніше з меню Help > Old-Style Macrofunctions вийти на довідкову сторінку Old-Style Macrofunctions (by Function), де репрезентовано всі їх категорії за функціональним призначенням (21 категорія). Якщо ж потрібно продивитися дані щодо відомої макрофункції, то зі сторінки Old-Style Macrofunctions (by Function) можна перейти на сторінку Old-Style Macrofunctions (by Number).

У цій лабораторній роботі розглядаються макрофункції двох категорій:

a)буфери(Buffers, рис. 2.2, а), зокрема, btri – еквівалентний примітиву TRIPrimitive з інверсним входом дозволу ОЕ, а також ІС, що містять по шість і вісім буферів з трьома станами виходу;

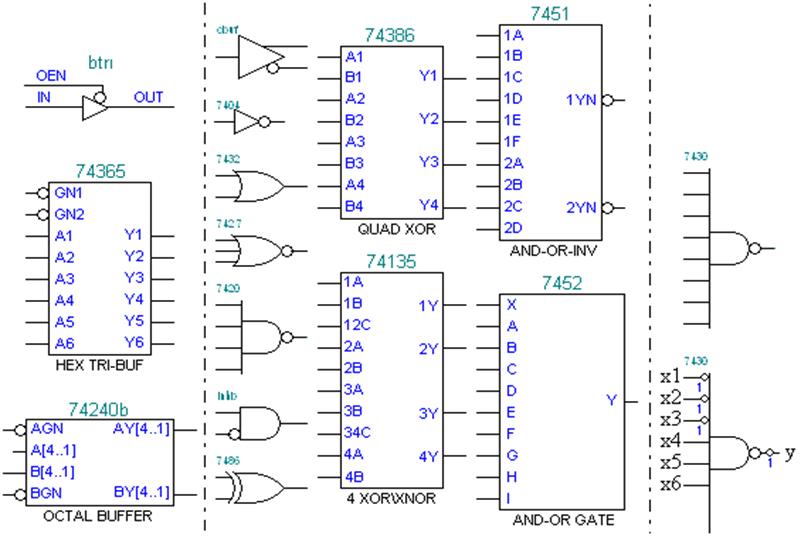
                    а)                                               б)                    в)

Рисунок 2.2 – Макрофункції: а) порти; б) буфери; в) логічні примітиви