б) у графічному файлі: ввести ім’я проекту > виділити порт чи інший елемент > меню Utilities > Timing Analysis Source – для джерела, Timing Analysis Destination – для адресата або Timing Analysis Cutoff – для вузла, який не треба враховувати в матриці; продовжуючи, визначити таким чином всі джерела та адресати.
в) Виконати п. 1.2.3.3, г), ґ), д), але матрицю у формі таблиці (з розширенням .tao) зберегти під іншим іменем, наприклад, 1det1.tao або 1det.tao1.
Контрольні питання та завдання
1. Які системи логічних функцій є функціонально повними? Які з них є мінімально повними? Доведіть, що мінімально повну систему утворюють: 1) операція заборони і константа одиниці, 2) операція імплікації і константа нуля.
2. Логічну функцію y здійснити на заданому елементі з використанням інверторів (далі наводиться варіант: функція – заданий елемент):
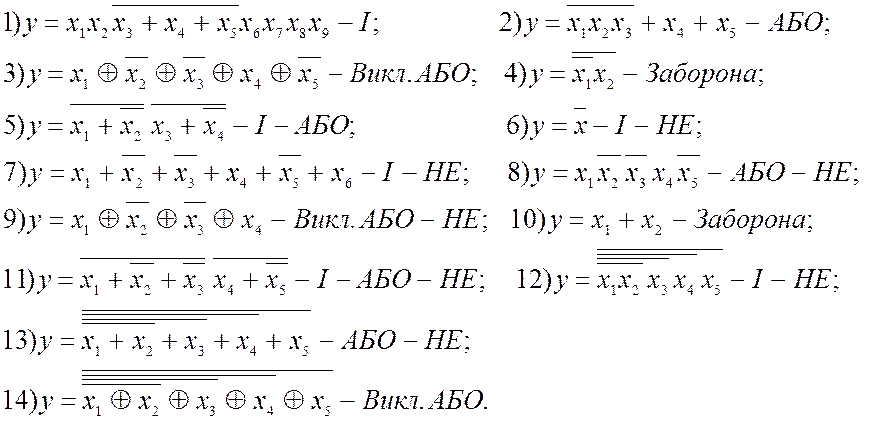
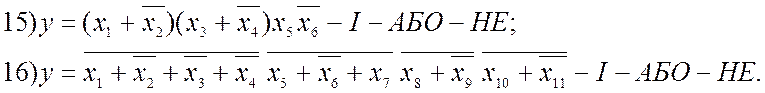
3. Який логічний елемент B (рис. 1.2, г) утворюється додаванням інверторів відповідно до рис. 1.2, а), б), в), якщо A є елемент: 1) АБО, 2) І, 3) Виключне АБО, 4) Заборона, 5) АБО-НЕ, 6) І-НЕ, 7) Виключне АБО-НЕ, 8) Імплікатор?

а) б) в) г)
Рисунок 1.2
2 РЕАЛІЗАЦІЯ ЛОГІЧНИХ ФУНКЦІЙ
Мета роботи: створення проекту за його графічного введення; засвоєння методики користування електронним довідником для добору потрібної ІС серії 74 і методики настроювання макрофункцій.
Домашнє завдання
! 1) Засвоїти теоретичні відомості щодомінімізації логічних функцій, реалізації їх у поширених базисах та способів спрощення логічних схем.
2) Для заданої згідно з варіантом (див. додаток А, варіанти завдання 2) логічної функції y: а) побудувати таблицю відповідності і діаграму термів (Вайча-Карно); б) навести досконалі (ДДНФ або ДКНФ) та мінімальні (МДНФ і МКНФ) форми; в) перетворити мінімальні форми до базисів І-НЕ, АБО-НЕ та І-АБО-НЕ; г) мінімізувати схему в базисі І-НЕ чи АБО-НЕ, який забезпечує меншу складність; ґ) навести схеми за підпунктами в), г).
2.1 Стислі теоретичні відомості
2.1.1 Мінімізація логічних функцій
Мінімізація логічних функцій полягає в перетворенні ДДНФ до мінімальної ДНФ (МДНФ) або ДКНФ до мінімальної КНФ (МКНФ) функції. Серед формалізованих методів мінімізації найбільшого поширення набув метод за допомогою діаграм термів(Вайча – Карно). Для функції yчотирьох змінних(рис. 2.1, а) клітинки діаграми термів (рис. 2.1, б) нумеруються десятковими кодами і вхідних кортежів. Стандартна нумерація клітинок полегшує заповнення власне діаграми функції y (рис. 2.1, в): до діаграми переносять лише одиниці з колонки y таблиці відповідності згідно з кодами i вхідних кортежів, а до порожніх клітинок вважаються записаними нулі, або, навпаки, переносять лише нулі (рис. 2.1, г), тоді порожні клітинки відповідають значенням y = 1.
Підсумовуванням мінтермів (сполучень одиниць) дістаємо шукану МДНФ у вигляді
![]()
Цю ж саму діаграму термів можна використати й для здобуття інверсної функції КНФ
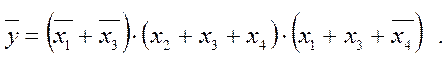
Підсумовуванням макстермів (сполучень нулів) дістаємо шукану МДНФ у вигляді
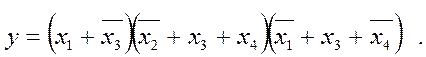
а) |
б) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
в) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
г) |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.