Лабораторний практикум з дослідження цифрових пристроїв на основі САПР MAX+PLUS II, страница 23

                                                 а)                               б)

Рисунок 3.4 – Принцип побудови шифратора

Принцип побудови і особливості проектування шифраторів розглянемо на прикладі перетворення 4-розрядного унітарного коду у двійковий: вибираємо кількість розрядів двійкового коду n = 2; складаємо скорочену таблицю відповідності (рис. 3.4, а), в якій зазначаємо лише припустимі набори змінних, бо в усіх інших із 2⁴ = 16 рядків таблиці буде міститися більш, ніж одна одиниця у вхідному коді; визначаємо рівняння вихідних функцій

 та будуємо схему (рис. 3.4, б).

На відміну від унітарного коду “1 із К”, у коді “Х із К” може міститися  довільна кількість  одиниць, проте вихідним кодом має  відображатися  лише одна з них, із найбільшим пріоритетом. Код “Х із К” можна також моделювати клавішами, коли можливе натиснення більш ніж однієї з них. Шифратор, що перетворює код “Х із К” у двійковий, називається пріоритетним. Крім вихідного коду Y він може формувати також сигнал запиту на обслуговування GS, який стає активним за надходження хоча б одного з вхідних сигналів. Бібліотека міститьпріоритетні шифратори 10:4 і 8:3 (рис. 3.5).

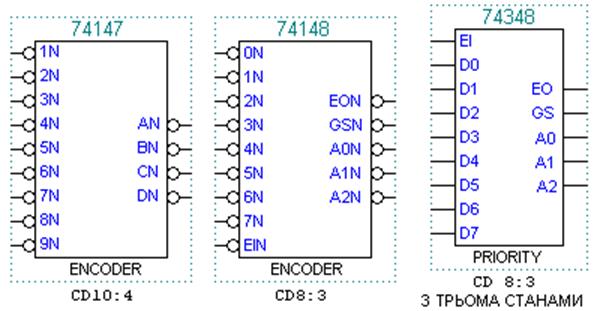
Рисунок 3.5 – Спеціалізовані макрофункції шифраторів

3.1.5 Елементи арифметики

3.1.5.1 Числа

Мовою AHDL застосовуються числа у звичайних системах числення (табл. 3.1) для зображення постійних значень (параметрів, змінних, номерів) в арифметичних і булевих виразах. При цьому значення набору змінних компілятор перетворює в послідовність двійкових цифр. Проте значення однієї змінної в булевих виразах не можна позначати числом, наприклад, замість виразів типу с = 0 або с = 1 слід вживати с = GND або с=VCC.

Таблиця 3.1

3.1.5.2 Групи

Низка однотипних елементів і їх назв для стислості може бути оголошена у вигляді окремого модуля, який  позначається символом групи. Наприклад, масив адресних сигналів і відповідних їм портів а3, а2, а1, а0 можна зобразити групою a[3..0].

3.1.5.3 Арифметичні оператори

Оператори використовуються в арифметичних виразах, щоб оцінити значення функцій, констант і параметрів а також виконати операції порівняння (в останньому випадку арифметичні оператори називають також компараторами). Такі вирази не потребують ресурсу ІС і призначені для зручності програмування; компілятор виконує обчислення і використовує лише результати – числа, які не можуть бути від’ємними. Основні арифметичні оператори і компаратори наведено в табл. 3.2.

Таблиця 3.2