З’єднувати шинами можна групи лише однакового діапазону, наприклад, з’єднання на рис. 4.4, а) означає, що мультиплексор має 4 адресні входи в групі sel[]. Нерозгалужену шину, як у цьому прикладі, можна не іменувати: розряди масивів а[] і sel[] з’єднуються відповідно до їх позицій у групах. Проте шина, що живить множину примітивів (рис. 4.4, г), має іменуватися, бо діапазон групи в її назві визначає їх кількість. У цьому прикладі перші входи 16-ти елементів І з’єднано із сигналами d15…d0, а на другі входи паралельно подано сигнал С.
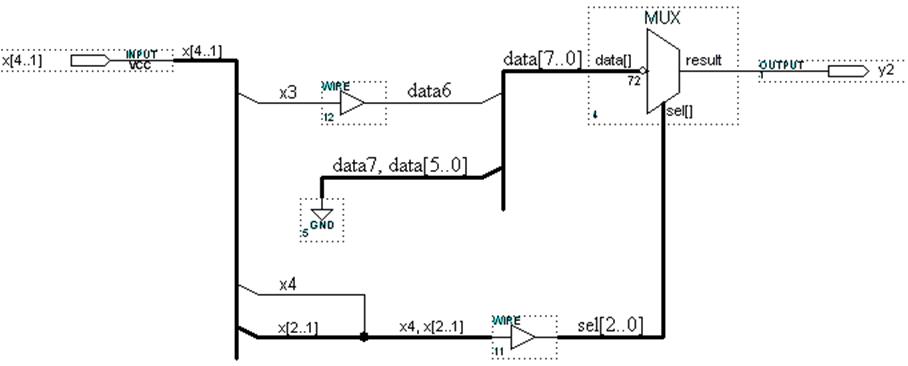
У випадку розгалужених шин мають іменуватися як шини, так і окремі лінії до і після місця розгалуження (рис. 4.4, ґ). При цьому імена шин і ліній мають збігатися з назвами з’єднуваних ними портів і вузлів (входів та виходів), тому, у разі потреби, імена узгоджують буферами Wire (рис. 4.4, д). Так, шина, що виходить з масиву портів x[4..1], має ту саму назву x[4..1], а шина, що з’єднує 8 інформаційних входів мультиплексора data[] з джерелами, також називається data[7..0]. Тому імена з’єднуваних ліній х3 і data6 узгоджуються буфером Wire.
F Примітки:
1. У графічному редакторі послідовні групи позначаються без дужок, наприклад, група у вигляді: data7, data[5..0] на рис. 4.4, д).
2. Стенографічне позначення типу sel[] є припустимим тільки в текстовому редакторі, а в графічному редакторі для шин завжди застосовується повне позначення групи типу sel[2..0].

а)
in[4..1] : INPUT;
б)

в)

г) д)
е)
Рисунок 4.4
3. Шини пов’язані з вузлами (компонентами) тільки іменами, тому з’єднання іменованих шин і ліній можна не зображати взагалі, їх зображають лише для наочності схеми. Отже, і точки з’єднань показувати необов’язково. Виняток становлять шини, на яких без точок з’єднань утворюються різні імена, як, наприклад, на нижній лінії рис. 4.4, е) без точки було б дві назви: “x[2..1]” i “x4, x[2..1]”.
4.1.3 Мегафункції
4.1.3.1 Означення мегафункції
Мегафункцією називається структурна модель у вигляді стандартного блоку високого рівня, що реально не існує, але після попереднього настроювання може використовуватися як компонент схеми поряд із примітивами і макрофункціями. Від макрофункції мегафункція відрізняється гнучкішими можливостями для настроювання параметрів і тим, що сигнали з’єднуються з нею, як правило, групами й шинами (вузли деяких різновидів макрофункцій також зображено шинами). Мегафункції містяться в директорії \maxplus2\max2lib\mega_lpm бібліотеки параметризованих модулів (LPM – Library of Parameterized Modules). До графічного файла мегафункція вставляється як звичайний елемент, але із зазначеної директорії, а до текстового редактора – за допомогою файла включення (.inc) оператором Include Statement.
Мегафункції поділяються на три основні і одну додаткову групи. Відомості про потрібну мегафункцію можна дістати з довідки: меню Help > Megafunctions/LPM > вибрати з групи і натиснути ім’я мегафункції. Схарактеризуємо стисло деякі різновиди мегафункцій, наведених у файлі 4libre_mega.gdf.
4.1.3.2 Логічні функції
|
а)
б) Рисунок 4.5 |
Мегафункції логічних елементів подано в категорії Gates (ворота). Мегафункція lpm_inv (рис. 4.5, а) є одновимірним масивом інверторів з параметром LPM_WIDTH, який визначає кількість входів і виходів. Якщо задати діапазон групи LPM_WIDTH= 3, еквівалентна схема набуває вигляду як на рис. 4.5, б). Інвертування входів і виходів здійснюється так само, як і в макрофункцій. Відмінність полягає тільки в тому, що інверсії задаються для всієї групи кодом (на символі відображається шістнадцятковий код, а вводити можна також двійковий або десятковий код). У цьому коді розряд, що інвертується, позначається одиницею, а який залишається без інверсії – нулем. У прикладі (див. рис. 4.5) подвійним запереченням (відображено кружком з шістнадцятковим числом 5 на виході символу мегафункції) усунуто інверсію розрядів х2 та х0 кодом 1012 = 516.
а)

б)
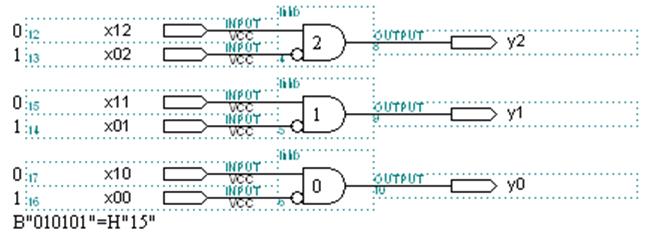
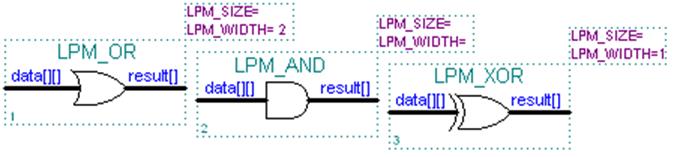
в)
Рисунок 4.6
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.