«Исследование физических свойств твердых тел», методические указания к лабораторным работам, страница 5

где G – модель сдвига; γ – относительная деформации сдвига.

Модуль сдвига связан с модулем упругости следующим соотношением

                                              ,                                    (10)

где μ – коэффициент Пуассона.

Коэффициент Пуассона для различных материалов находится в пределах 0,2 – 0,5.

Из гармонического приближения непосредственно следует закон Гука, описывающий упругую деформацию твердых тел. Это же приближение было положено в основу рассмотрения тепловых колебаний решетки и построения теории решеточной теплоемкости твердых тел, которая достаточно хорошо согласуется с опытом.

Однако с точки зрения гармонического приближения оказалось невозможным объяснить ряд хорошо известных явлений, таких, например, как тепловое расширение твердых тел, их теплопроводность и др.

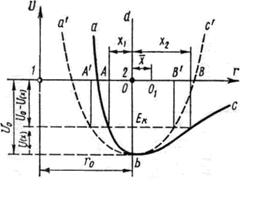
Рис.2. Зависимость потенциальной энергии взаимодействия частиц твёрдого тела от расстояния между ними.

Рассмотрим кривую зависимости потенциальной энергии взаимодействия частиц твердого тела от расстояния между ними (рис. 2). При абсолютном нуле частицы располагаются на расстояниях г₀, отвечающих минимуму энергии взаимодействия U₀ (на дне потенциальной ямы abc). Эти расстояния определяют размер тела при абсолютном нуле. С повышением температуры частицы начинают колебаться около положений равновесия О. Ради простоты допустим, что частица 1 закреплена неподвижно и колеблется лишь частица 2. Колеблющаяся частица обладает кинетической энергией, достигающей наибольшего значения Е_К в момент прохождения ею положения равновесия О. На рис. 2. энергия Е_К отложена вверх от дна потенциальной ямы. При движении частицы 2 влево от положения равновесия кинетическая энергия расходуется на преодоление сил отталкивания ее от частицы 1 и переходит в потенциальную энергию взаимодействия частицы. Отклонение влево происходит до тех пор, пока вся кинетическая энергия частицы Е_К не перейдет в потенциальную энергию. Последняя увеличится на U(х) = Е_К и станет равной –[U₀–U(х)], а частица 2 сместится предельно влево на расстояние х₁. При движении частицы 2 вправо от положения равновесия кинетическая энергия расходуется на преодоление сил притяжения ее к частице 1 и также переходит в потенциальную энергию взаимодействия частиц. В точке В, отстоящей от положения равновесия на расстоянии х₂, вся кинетическая энергия Е_К переходит в потенциальную, вследствие чего последняя увеличивается на U(х) = E_K и становится равной –[U₀–U(х)].