«Исследование физических свойств твердых тел», методические указания к лабораторным работам, страница 3

Шпиндель подвижной системы должен быть заарретирован при отсутствии в блоке испытуемого образца от арретира при установленном образце.

2. ДОМАШНИЕ ЗАДАНИЯ И МЕТОДИЧЕСКИЕ

УКАЗАНИЯ ПО ИХ ВЫПОЛНЕНИЮ

2.1. Задание № 1

Изучить взаимосвязь термического расширения твердых тел с особенностями межатомных взаимодействий. Рассмотреть феноменологические уравнения Грюнайаена. В заготовку отчёта занести основные уравнения и рис. 1,2,3.

Методические указания по выполнению первого задания

Для выполнения задания необходимо ознакомиться с материалом / 1, с. 201-208/.

Взаимодействие атомов твёрдого тела складывается из сил приближения и отталкивания.

При воздействии внешней растягивающей нагрузки расстояние между атомами увеличивается и равновесное расположение их в кристалле нарушается. Это приводит к нарушению равенства сил притяжения и отталкивания, характерного для равновесного состояния атомов в решетке, и возникновению внутренних сил, стремящихся вернуть атомы в первоначальные положения равновесия. Величину этих сил, рассчитанную на единицу площади поперечного сечения кристалла, называют напряжением.

Энергия взаимодействия частиц 1 и 2 в твердом теле является функцией расстояния r между ними и описывается кривой U(r), схематически показанной на рис. 1. При смещении частицы 2 из положения равновесия на расстояние х, т.е. при увеличении расстояния между частицами до r = r₀ + х, энергия частицы увеличивается, становясь равной U(r). Изменение энергии U(х) = U (r) — U(r₀) можно найти, разлагая U(r) в ряд Тейлора по степеням х:

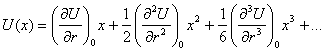                          (1)

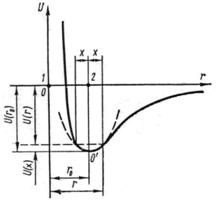
Рис.1. Потенциальная энергия взаимодействия двух атомов.

Ограничиваясь квадратичным членом разложения и учитывая, что  в точке О' равна нулю, находим

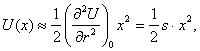                                                         (2)

Это приближенное выражение для изменения энергии частицы вследствие смещения ее из положения равновесия на расстояние х. Приближенным оно является потому, что в разложении (1) мы ограничились квадратичным членом и отбросили члены более высокого порядка. Графически зависимость в таком приближении выражается параболой, показанной на рис. 1. пунктиром.