«Исследование физических свойств твердых тел», методические указания к лабораторным работам, страница 26

Зная длину образца (L_l = 48мм, L_t = 47мм), легко рассчитать скорость продольной и сдвиговой волны

                                                                          (21)

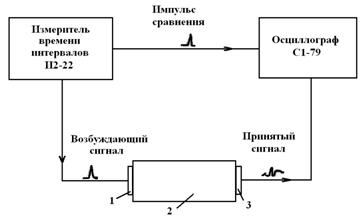
Рис.5. Схема установки для измерения скорости объемных волн (1 – излучатель, 2 – исследуемый образец, 3 – приемник)

Зная плотность стекла (ρ = 2500 кг/м ), по формулам (11) – (13) рассчитать модуль Юнга, сдвига и коэффициент Пуассона.

4.3. Задание №3

Определить коэффициент поглощения продольной α_l и сдвиговой α_t волны в стекле.

Коэффициент поглощения ультразвука обычно выражается в децибелах на сантиметр (дБ/см) и рассчитывается по выражению

где U₁ - амплитуда волны после прохождения в среде пути L₁; U₂ – амплитуда волны после прохождения пути L₂.

Амплитуда U₁ определяется по осциллографу по первому принятому сигналу; амплитуда U₂ – по величине сигнала, испытавшего отражение в образце, т.е. прошедшего путь , Амплитуда импульсов определяется визуально на сетке осциллографа по размаху колебаний.

4.4. Задание №4

Снять температурную зависимость времени задержки распространения продольной волны в стекле в диапазоне температур 20 – 80 ºC

Рассчитать температурный коэффициент скорости распространения продольной волны (ТКС_l).

Для измерения температурной зависимости подключить измерительную схему к образцу, находящемуся в термошкафу. Включить термошкаф и измерить задержку через 20 градусов до 80 °С. Построить график зависимости C_l от температуры (длина образца в термошкафу 101 мм)

Определить ТКЗ_l в диапазоне 20 – 80 ºC по формуле:

,

где  и  – время задержки при температурах 20 °С и 80 °С соответственно (T₁ и T₂)