Подставляя выражение US в уравнение (а) и разрешая его относительно Uвых, имеем
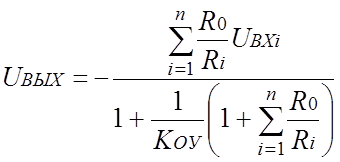 (б)
(б)
Так как
Коу=105 ¸ 106, то величина![]()
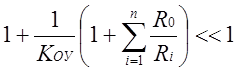 .
Пренебрегая этой величиной в знаменателе уравнения (б), получаем
.
Пренебрегая этой величиной в знаменателе уравнения (б), получаем
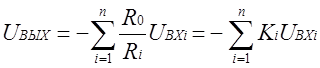 ;
(1.3)
;
(1.3)
где
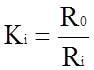 .
.
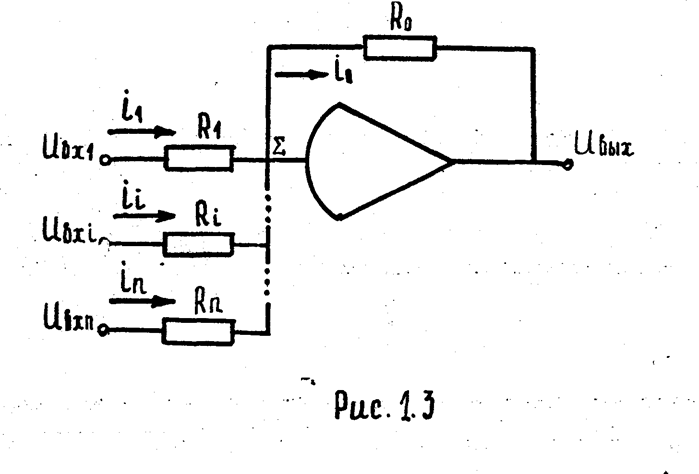
Таким
образом, рассмотренный решающий усилитель суммирует входные напряжения с
одновременным умножением их на постоянные коэффициенты. Такой решающий
усилитель называется сумматором. Величина 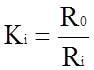 называется
коэффициентом передачи сумматора по i -ому входу.
называется
коэффициентом передачи сумматора по i -ому входу.
Замечание.
Пренебрежение величиной 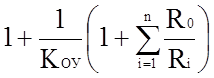
при выводе
уравнение (1.3) равносильно принятию допущения KОУ=¥ или 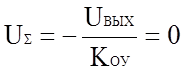
![]() При допущении US=0 уравнение (1.3 ) непосредственно следовало из уравнения (а). В
дальнейшем будем принимать непосредственно допущение US=0.
При допущении US=0 уравнение (1.3 ) непосредственно следовало из уравнения (а). В
дальнейшем будем принимать непосредственно допущение US=0.
Частные случаи.
1) n=1 Уравнение (1.3) принимает вид
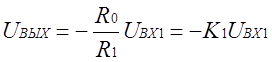 (1.4)
(1.4)
Решающий усилитель умножает входное напряжение на постоянный коэффициент и называется масштабным.
2) n=1 и R1=R0. Уравнение (1.3) принимает вид
UВЫХ=-UВХ
Решающий усилитель изменяет знак входного напряжения и называется инвертором.
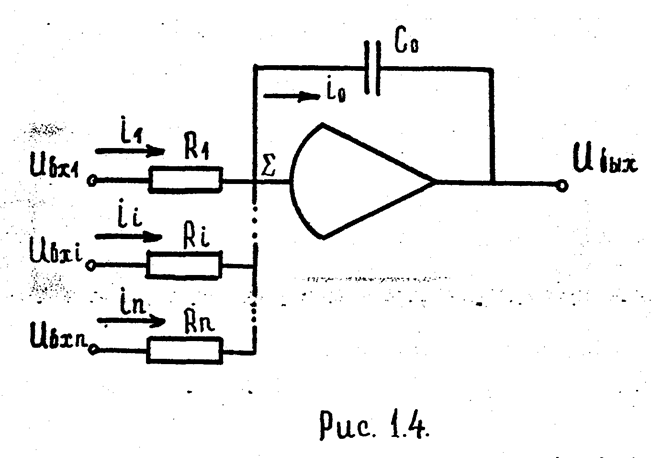
2. Интегратор - сумматор.
На рис. 1.4 изображена схема решающего усилителя, у которого элементом Zi является резистор Ri , а элементом Z0- конденсатор емкостью С0
В
рассматриваемом случае токи ii и i0 определяются
выражениями 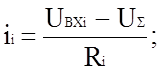
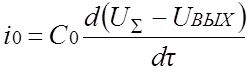 .
.
Согласно уравнению (1.2)
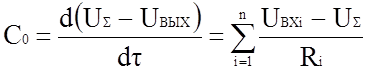 ,
,
откуда, полагая US =0, имеем
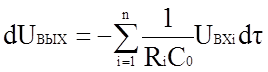
Интегрируя это уравнение в пределах: UВЫХ от UВЫХ(0) до UВЫХ,
t от 0 до t получаем
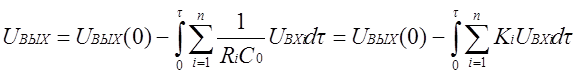 . (1.6)
. (1.6)
При UВЫХ(0)=0 уравнение (1.6) имеет вид
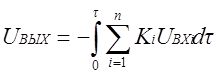 (1.6а)
(1.6а)
или в операторной форме
![]()
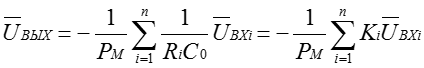 ;
(1.6б)
;
(1.6б)
где 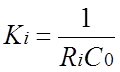 .
.
Таким
образом, рассмотренный решающий усилитель интегрирует сумму входных напряжений,
умноженных на постоянные коэффициенты, Такой решающий усилитель называется
интегратором-сумматором. Величина 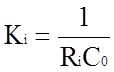 называется
коэффициентом передачи интегратора-сумматора по i-му входу.
называется
коэффициентом передачи интегратора-сумматора по i-му входу.
В случае n=1 уравнения (1.6) и (1.6 а,б) принимают вид:
![]()
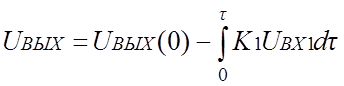 ,
(1.7)
,
(1.7)
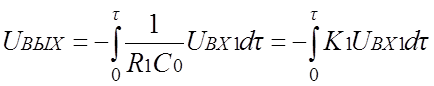 ,
(1.7a)
,
(1.7a)
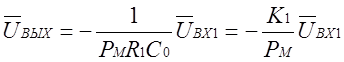 .
(1.7б)
.
(1.7б)
Такой решающий усилитель называется интегратором.
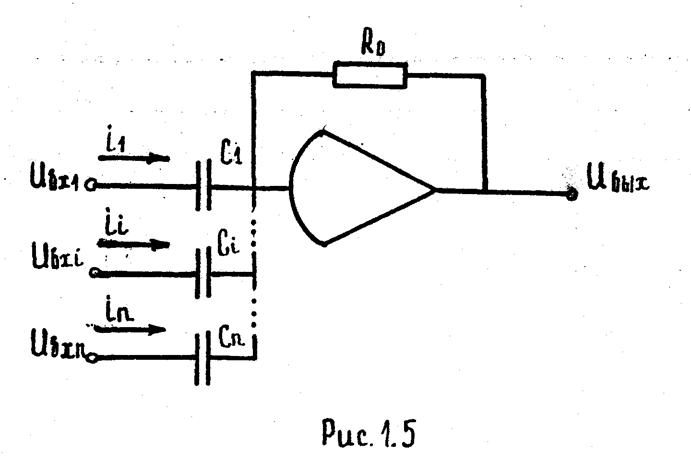
3. Дифференцирующий усилитель.
На рис. 1.5 изображена схема решающего усилителя, у которого элементом Zi является конденсатор ёмкостью Сi, а элементом Zi- резистор R0.
В рассматриваемом случае токи ii и i0
определяются выражениями 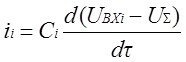 ;
;
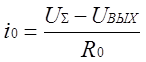 .
.
Согласно уравнению (1.2)
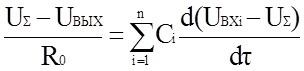
откуда, полагая US = 0, имеем
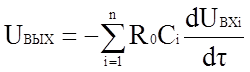
Меняя порядок выполнения операций, получаем
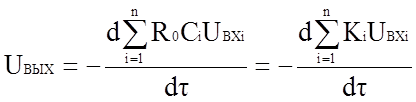 ,
(1.8)
,
(1.8)
или в операторной форме
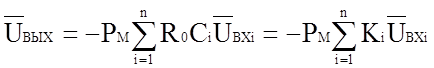 , (1.8а)
, (1.8а)
где Ki=R0Ci
Таким образом, рассмотренный решающий элемент дифференцирует сумму входных напряжений, умноженных на постоянные коэффициенты. Такой решающий усилитель называется дифференцирующим. Величина Ki=R0Ci называется коэффициентом передачи дифференцирующего усилителя по i-му входу.
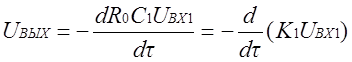 ,
(1.9)
,
(1.9)
![]() . (1.9a)
. (1.9a)
Замечание. При моделировании по возможности избегают применения дифференцирующих усилителей вследствие их повышенной чувствительности к помехам.
План лекции.
1. Общее уравнение РУ.
2. Решение с помощью РУ линейных дифференциальных уравнений с нулевыми начальными условиями.
1.3. Общее уравнение решающего усилителя.
В общем случае токи ii и i0 (см. рис. 1.2) определяются выражениями
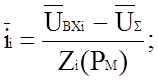
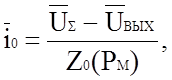
где Zi(PМ) - комплексное сопротивление элемента Zi;
Z0(PМ)- комплексное сопротивление элемента Z0.
Согласно уравнению (1.2)
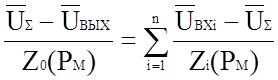
откуда, полагая ![]() , получаем
, получаем
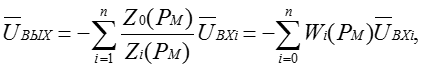 (1.10)
(1.10)
где 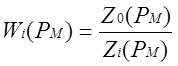 .
(1.11)
.
(1.11)
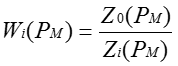 называется
передаточной функцией решающего усилителя по i-тому входу.
называется
передаточной функцией решающего усилителя по i-тому входу.В случае n=1 уравнение (1.10) принимает вид
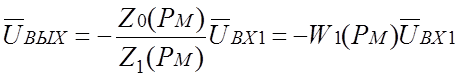 (1.12)
(1.12)
Частными случаями уравнения (1.10) являются уравнения (1.3),
(1.6б) и (1.8а). Действительно: для сумматора Z0(PМ)=R0,
Zi(PМ)=Ri и из уравнения (1.10) следует
уравнение (1.3); для интегратора-сумматора 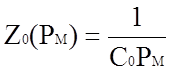 ,
Zi(PМ)=Ri и из уравнения (1.10) следует
уравнение (1.6б); для дифференцирующего усилителя Z0(PМ)=R0,
,
Zi(PМ)=Ri и из уравнения (1.10) следует
уравнение (1.6б); для дифференцирующего усилителя Z0(PМ)=R0,
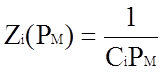 и из уравнения (1.10) следует
уравнение (1.8а).
и из уравнения (1.10) следует
уравнение (1.8а).
Частными случаями уравнения (1.12) являются уравнения (1.4), (1.7а) и (1.9а).
Элементами Zi и Z0 могут являться не только резисторы и конденсаторы, но и различные цепи из резисторов и конденсаторов. Схемы и комплексные сопротивления Z(PМ) таких цепей приведены в таблице 1.1 (таблица 1.1 находится в файле tabl2a.doc)
С помощью решающего усилителя, у которого элементами Zi и Z0 являются цепи из резисторов и конденсаторов, можно решать линейные дифференциальные уравнения с нулевыми начальными условиями. Рассмотрим несколько схем таких решающих усилителей.
I). На рис. 1.6 изображена схема решающего усилителя, у которого элементами Zi и Z0 являются цепи, значащиеся в таблице I.I соответственно под № I и №3. Из таблицы следует, что
Z1(PМ)=R1;
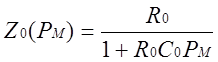 .
.
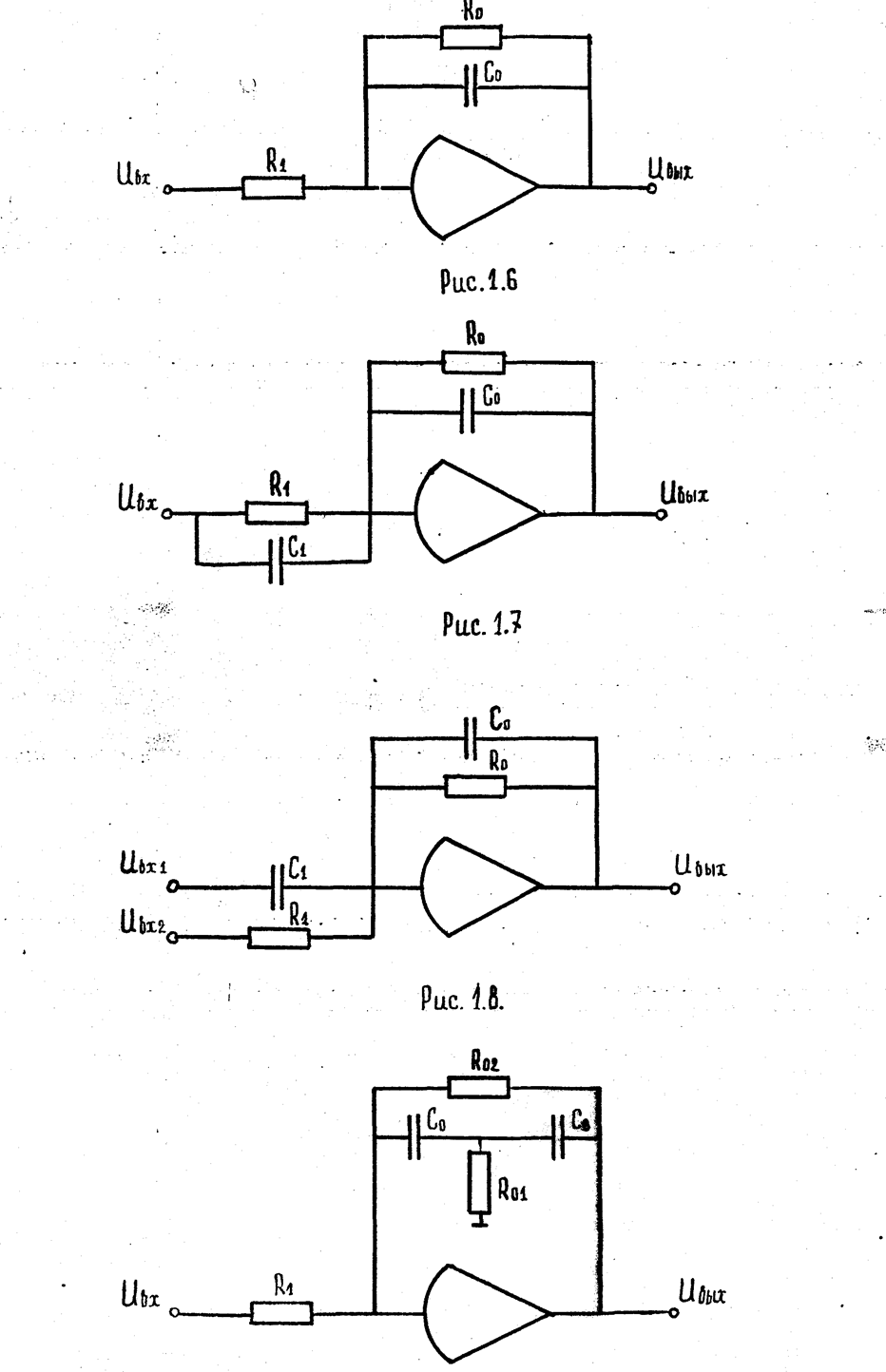
Подставляя выражения z1(pM) и z0(pM) в уравнение (1.12), получаем
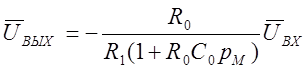 (1.13)
(1.13)
или
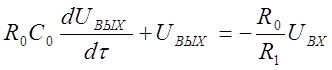 (1.13a)
(1.13a)
Рассмотренный решающий усилитель называется инерционным,
2) На рис. 1.7. изображена схема решающего усилитителя, у которого элементами Z1 и Z2 являются цепи, значащиеся в таблице 1.1. под № 3. Из таблицы следует, что
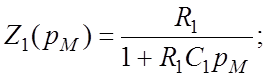
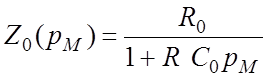
Подставляя выражения Z1(pM) и Z0(pM) в уравнение (I.I2), получаем
или:
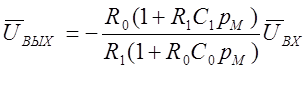 (1.14)
(1.14)
или:
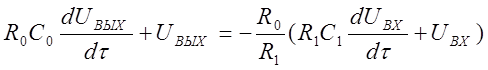 (1.14a)
(1.14a)
3) На рис. 1.8 изображена схема решающего усилителя, у которого элементами Zi и Z0 являются цепи, значащиеся в таблице 1.1. соответственно под №1, №2, и №3. Из таблицы следует, что
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.