Основы математического и физического моделирования систем управления, страница 25

По структурной схеме (рис. 4.5) для каждого нелинейного решающего элемента составляем уравнение, связывающее выходное и входное напряжения:

(МУ)

(ДУ)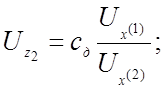

(ФП № 1)

(ФП № 2)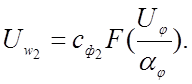

Сопоставляя полученные уравнения с соответствующими машинными уравнениями, выражаем коэффициент передачи нелинейных решающих элементов через масштабы преобразования переменных:

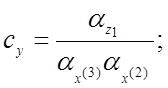
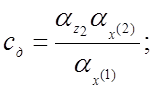                                              (4.24)

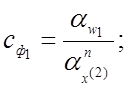
Анализируя уравнения (4.24) и структурную схему (рис. 4.5), можно сформулировать следующие правила, позволяющие выразить коэффициенты передач нелинейных решающих элементов через масштабы преобразования переменных:

1) коэффициент передачи множительного устройства равен масштабу преобразования произведения, деленному на произведение масштабов преобразования сомножителей;

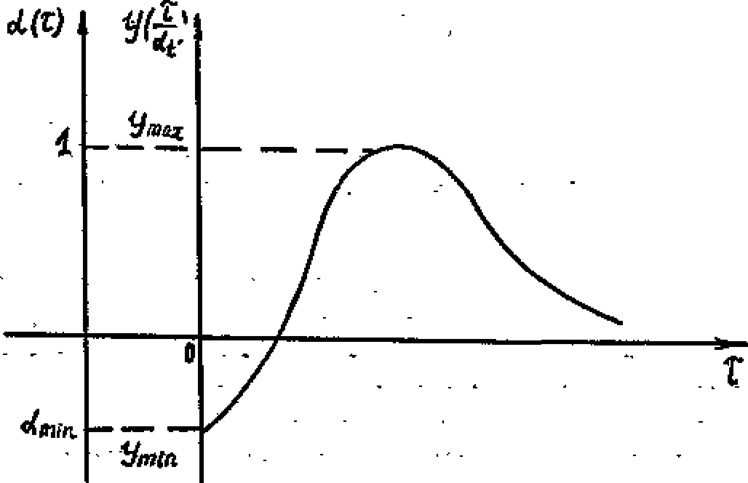
Рис. 4.4

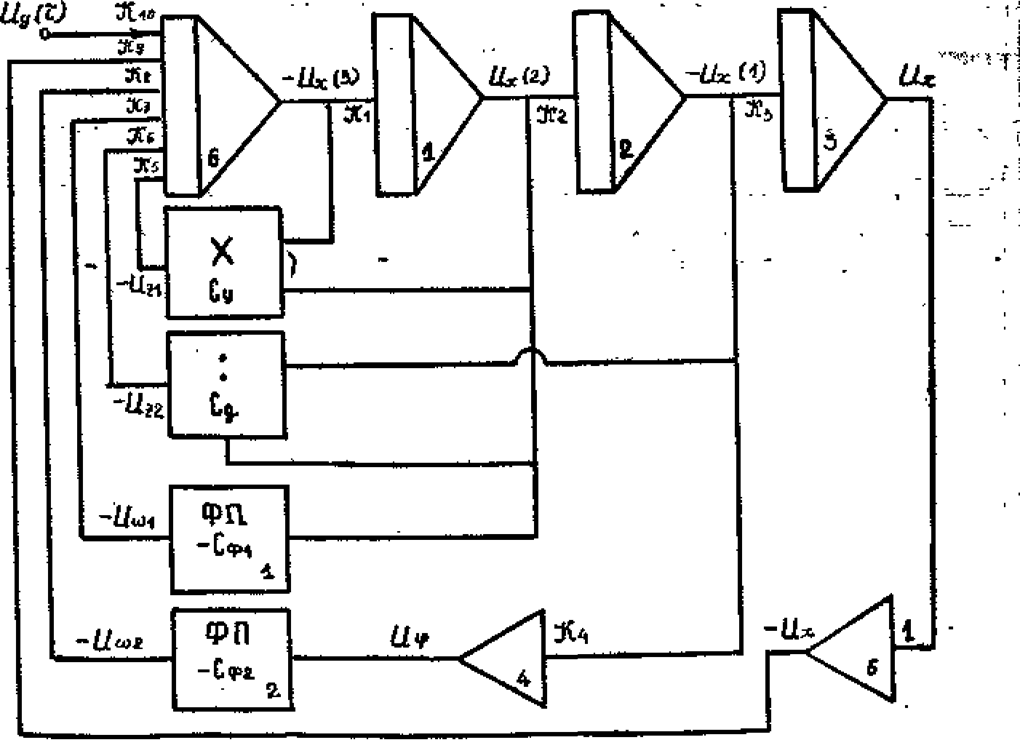
рис. 4.5

2)коэффициент передачи делительного устройства равен произведению масштабов преобразования частного и делителя, делённому на масштаб преобразования делимого;

3)коэффициент передачи функционального преобразователя, воспроизводящего n–ю степенную функцию, равен масштабу преобразования функции, делённому на масштаб преобразования аргумента в степени n;

4)коэффициент передачи функционального преобразователя, воспроизводящего трансцендентную или неаналитическую функцию, равен масштабу преобразования функции.

Получим соотношения между коэффициентами передачи решающих элементов, масштабами преобразования переменных и коэффициентами исходного уравнения.

По структурной схеме (рис. 4.5) для каждого решающего элемента составляем уравнение, связывающее выходное и входные напряжения.

(№6) 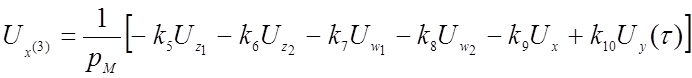,      (4.25)

 

(МУ)

(ДУ) 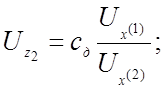                                            (4.26)

(ФП № 1)

(ФП № 2)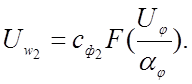

(№ 4)                                         (4.26а)

(№ 1)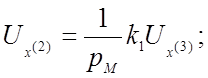

(№ 2)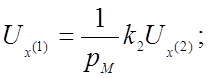

(№ 3)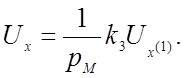

Из уравнений (4.25), (4.26) и (4.26а) исключаем напряжения, соответствующие производным:

 

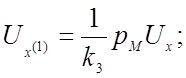
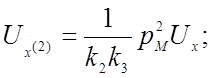
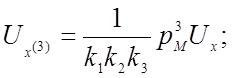
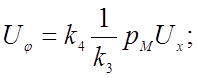
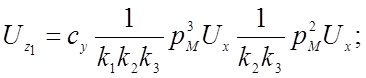
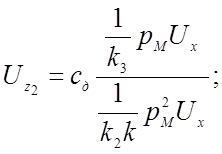
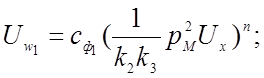
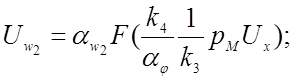
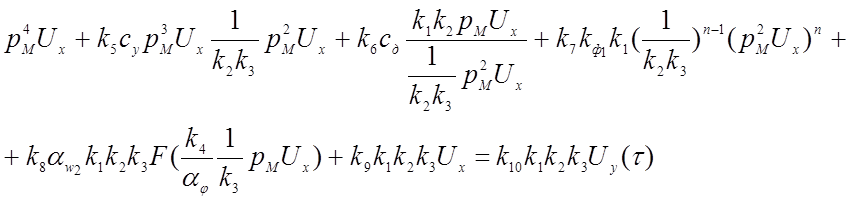
(№ 2)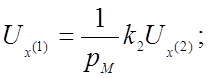

(№ 3)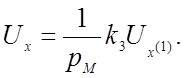

Из уравнений (4.25), (4.26) и (4.26а) исключаем напряжения, соответствующие производным:

 

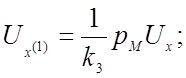
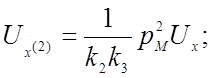
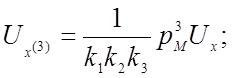
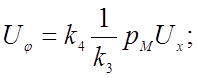
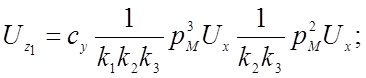
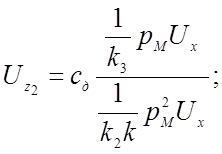
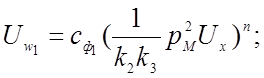
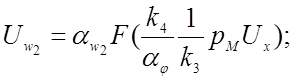
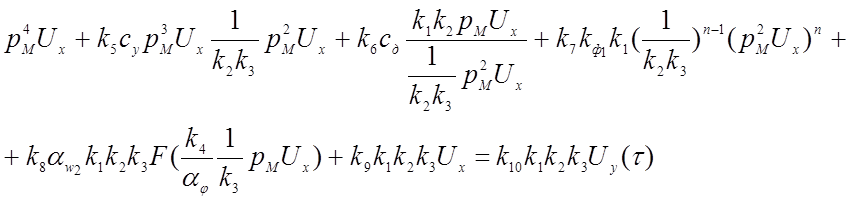
Заменяем в уравнении (4.27) машинные переменные исходными переменными, используя  уравнения преобразования (4.1а) и (4.2):

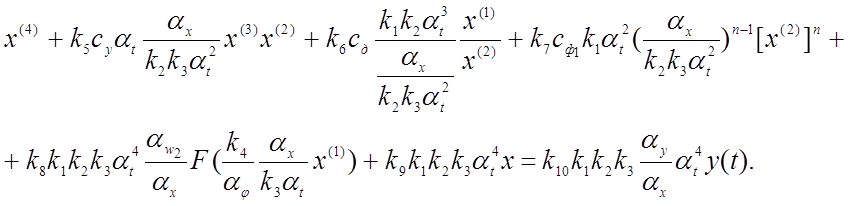
Сопоставляя полученное уравнение с исходным уравнением (4.23), получаем соотношения между коэффициентами передачи решающих элементов, масштабами преобразования переменных и коэффициентами исходного уравнения:

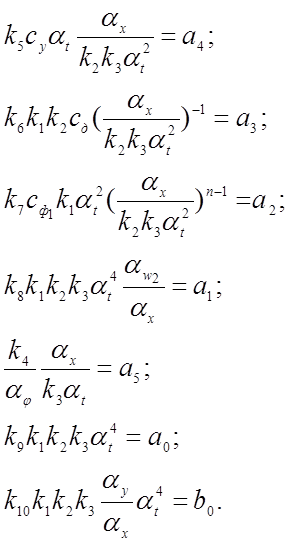                                  (4.28)

Анализируя уравнения (4.28), структурную схему (рис. 4.5) и исходное уравнение (4.23), можно сформулировать следующие правила, позволяющие получать соотношения между коэффициентами исходного уравнения при нелинейных членах, коэффициентами передачи решающих элементов и масштабами преобразования переменных.

1. Коэффициент исходного уравнения при произведении, частном или степенной функции равен произведению двух сомножителей:

а) первый сомножитель выражается так же, как и коэффициент исходного уравнения при линейном члене, причём для коэффициента при произведении берется контур, на выходе которого получается напряжение, соответствующее сомножителю большего порядка, а для коэффициента при частном берется контур, на выходе которого получается напряжение, соответствующее делимому,

б) второй сомножитель равен масштабу преобразования искомой переменной, делённому на произведение коэффициентов передачи интегрирующих усилителей, последовательно включенных в цепь между второй точкой подключения обратной связи и выходом искомой переменной, и на масштаб времени в степени, равной числу интегрирующих усилителей в этой цепи;

в) второй сомножитель возводится в степень N, причём для коэффициента при произведении N=1, для коэффициента при частном N=-1, для коэффициента при степенной функции N=n-1.

2. Коэффициент исходного уравнения при трансцендентной или неаналитической функции выражается так же, как и коэффициент исходного уравнения при независимой переменной (внешнем возмущении) y(t).

3. Коэффициент исходного уравнения при переменной аргумента трансцендентной или неаналитической функции равен произведению двух сомножителей:

а) первый сомножитель равен отношению коэффициента передачи масштабного усилителя, на выходе которого получается напряжение, соответствующее аргументу функции, к масштабу преобразования аргумента функции;

           б) второй сомножитель равен масштабу преобразования исходной переменной, делённому на произведение коэффициентов передачи интегрирующих усилителей, последовательно включенных в цепь между точкой подключения обратной связи и выходом искомой переменной, и на масштаб времени в степени, равной числу интегрирующих усилителей в этой цепи.

Лекция №27

План

1. Особенности подготовки к решению на АВМ дифференциального уравнения с переменными во времени коэффициентами.

2. Особенности подготовки системы дифференциальных уравнений к решению на АВМ.

4.7. Особенности подготовки дифференциального уравнения с переменными во времени коэффициентами к решению на АВМ.

Подготовка дифференциального уравнения с переменными во времени коэффициентами производится, в основном, так же, как и подготовка дифференциального уравнения с постоянными коэффициентами. При этом переменные во времени коэффициенты  целесообразно представить соотношением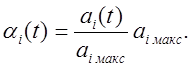 

Рассмотрим пример подготовки дифференциального уравне­ния с переменными во времени коэффициентами. Пусть для решения на АВМ задано линейное дифференциальное уравнение 2-го порядка с переменными во времени коэффициентами:

                              (4.29)

Преобразуем уравнение (4.29)

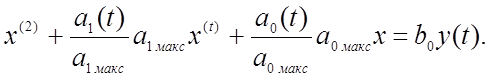                      (4.29а)

Получаем систему машинных уравнений

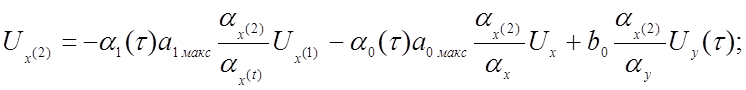
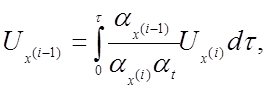
где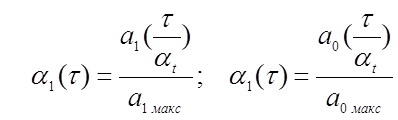

Составляем структурную схему модели (рис. 4.5).