С появлением полупроводниковых интегральных схем, в нашей стране стали выпускать АВМ третьего поколения: аналоговые вычислительные комплексы ABK-3I, АВК-32, АВК-33, ЭМУ-200.
Особенно значение аналоговых средств моделирования возрастает при аналого-цифровых методах исследования САУ. За последние 25-30 лет средства аналоговой техники прошли огромный путь, охватывающий следующие основные этапы их развития: аналоговые машины, работающие в режиме одноразового решения; аналоговые машины с периодизацией решения; итеративные аналоговые машины; аналоговые машины, дополненные средствами запоминания и хранения информации, сложными системами программного управления и устройствами для образования и измерения статистических характеристик; наконец, аналого-цифровые вычислительные системы (АЦВС). В АЦВМ и АЦВС два вида моделирования (аналоговое и цифровое) взаимно дополняют друг друга. Первые попытки объединить АВМ и ЦВМ с целью решения таких задач, которые сложно было реализовать на отдельно взятых машинах, были сделаны в конце 50-х годов. В последние годы достигнуты значительные успехи в области построения АЦВС. Ученые СССР, США и других стран разработали новое поколение АЦВС, которые являются весьма эффективным средством моделирования. Это, например: ГВС-100 (СССР, СФРЮ), АЦВС "Русалка"; АЦВК-3, АЦВК-ЗЕС, АЦВК-31, АЦВК-32, АЦВК-33 (СССР), система HRS -860 (ФРГ), семейство систем PACER и EAJ -2000 (США) и др.
Достоинствами АВМ являются простота подготовки задачи к решению, быстрота решения задачи, простота изменения параметров и начальных условий, высокая наглядность решения. Длительность решения задачи на АВМ зависит от выбранного масштаба времени и не зависит от сложности задачи, так как все математические операции выполняются одновременно. В зависимости от выбранного масштаба времени скорость процесса, протекающего в модели, может быть равна, больше или меньше скорости процесса, протекающего в оригинале. Масштаб времени выбирается с таким расчетом, чтобы длительность решения задачи не превышала определенной для каждой АВМ величины. Для большинства АВМ эта величина лежит в пределах 150 - 2000 сек.
Недостатком АВМ является невысокая точность решения задачи. Точность решения задачи на АВМ определяется точностью выполнения математических операций решающими элементами, входящими в её состав. Погрешность результатов может составлять несколько процентов от максимальных значений величин. Даже для наиболее точных АВМ погрешность результатов - не менее 0,1%.
В настоящее время определились два направления совершенствования аналоговой вычислительной техники. Первое - улучшение структуры и архитектуры АВМ; использование более совершенных элементов и блоков; второе - создание АВМ на базе специальных микропроцессоров (больших интегральных схем) для обработки аналоговых сигналов. В связи с этим ожидается увеличение точности решения задач почти на порядок по сравнению с АВМ третьего поколения.
1. Определение линейных решающих элементов.
2. Решающий усилитель, функциональная схема РУ.
3. Суммирующий, интегрирующий и дифференцирующий усилитель.
РАЗДЕЛ I. РЕШАЮЩИЕ ЭЛЕМЕНТЫ АВМ.
Глава I. ЛИНЕЙНЫЕ РЕШАЮЩИЕ ЭЛЕМЕНТЫ.
1.1. Функциональная схема решающего усилителя и исходные зависимости.
Линейными решающими элементами называются такие решающие элементы, для которых связь между выходным и входными напряжениями описывается линейным уравнением.
Рассмотрим основные линейные решающие элементы АВМ - решающие усилители.
Решающий усилитель представляет собой операционный усилитель (ОУ) о большим коэффициентом усиления (Коу- 105 – 106), охваченный отрицательной обратной связью.
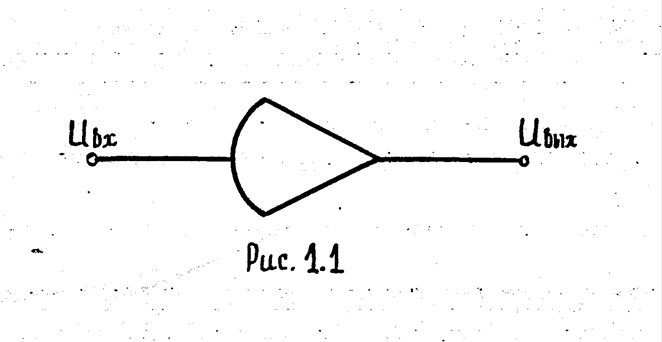
Большинство современных ОУ построены по схеме дифференциального усилителя, имеют один несимметричный выход и два дифференциальных входа по отношению к общему проводу ("земля"). Коэффициенты усиления по каждому входу равны, но противоположны по знаку. Вход, отмеченный знаком "минус", называется инвертирующим. Вход отмеченный знаком "плюс", неинвертирующий. Для обеспечения отрицательной обратной связи в ОУ используется инвертирующий вход. На схемах аналогового моделирования неиспользуемый неинвертирующий вход опускается, и общий для входа и выхода провод не изображается, т.е. используется условное изображение ОУ, приведенное на рис. I.I.
Для ОУ справедлива зависимость
UВЫХ= - КОУUВХ,
где КОУ -коэффициент усиления ОУ без обратной связи.
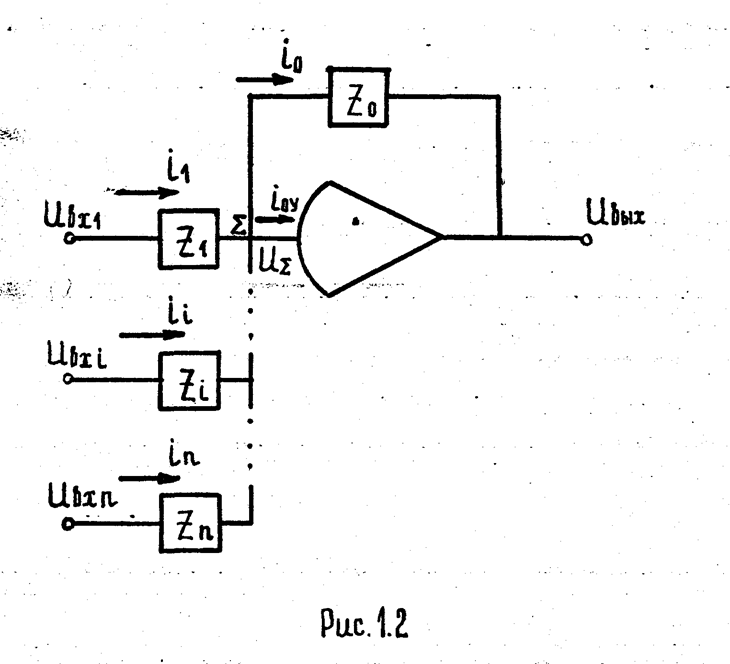
На рис. 1.2. изображена функциональная схема решающего усилителя. Усилитель имеет n входов и один выход. Величинами UВXi и UВЫХ обозначены соответственно напряжение на i -том входе и напряжение на выходе. Отрицательная обратная связь осуществлена соединением выхода ОУ с его инвертирующим входом. Элементами Zi и Z0 обозначены соответственно элемент, включенный в i -ую входную цепь, и элемент, включенный в цепь обратной связи. Элементами Zi и Z0 могут являться резисторы, конденсаторы и различные цепи из резисторов и конденсаторов. Величинами ii, i0, iоу обозначены соответственно ток, протекающий по i-той входной цепи, ток протекающий по цепи обратной связи, и ток в ОУ.
Применяя первый закон Кирхгофа к точке " å ", имеем
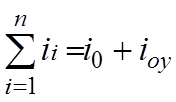
Т.к. ОУ имеет большое собственное входное сопротивление, то величина iоу=0. Пренебрегая этой величиной получаем
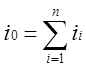 (1.2)
(1.2)
Зависимости (I.I) и (1.2) являются исходными для получения уравнений, описывающих связь между выходным и входными напряжениями решающих усилителей.
1.2. Выполнение элементарных математических операций с помощью решающего усилителя.
С помощью решающего усилителя, у которого элементами Zi и Z0 являются резисторы и конденсаторы, можно выполнять элементарные математические операции. Рассмотрим схему таких решающих усилителей.
I. Сумматор.
На рис. 1.3. изображена схема решающего усилителя, у которого элементом Zi является резистор Ri, а элементом Z0 - резистор R0.'
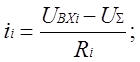
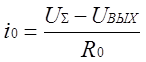 ;
;
где
US - напряжение в точке S.
Согласно уравнению (1.2)
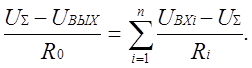 (а)
(а)
Согласно уравнению (I.I)
![]()
откуда
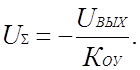
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.