Согласно уравнению (1.11) (см. разд. I) передаточная функция решающего усилителя с "R-С" цепями во входной цепи и в цепи обратной связи
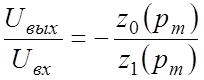 ,
,
где ![]() - сопротивление входной "R-C"
цепи,
- сопротивление входной "R-C"
цепи,
![]() - сопротивление "R-C"
цепи обратной связи.
- сопротивление "R-C"
цепи обратной связи.
Схемы
"R-С" цепей и их сопротивления ![]() приведены
в таблице 2 (см. раздел 1).
приведены
в таблице 2 (см. раздел 1).
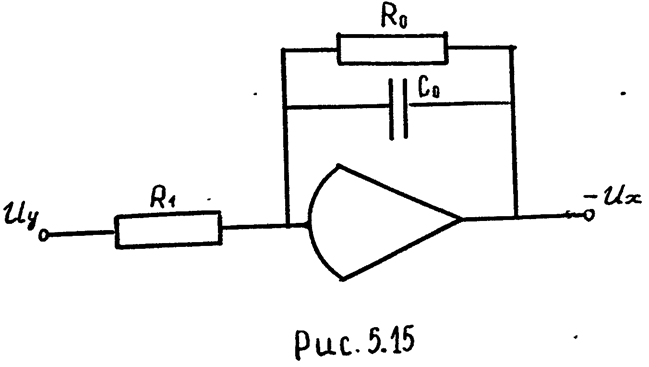
1) Схема модели апериодического звена (рис. 5,15). Машинная передаточная функция (см. уравнение (5.6))
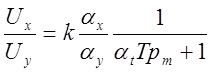 .
.
Из табл. 2 берем цепи №1 и №3 и их сопротивления
![]() ;
; 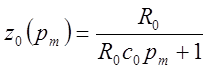
Следовательно,
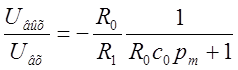
Очевидно,
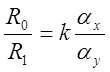 ;
; ![]() .
.
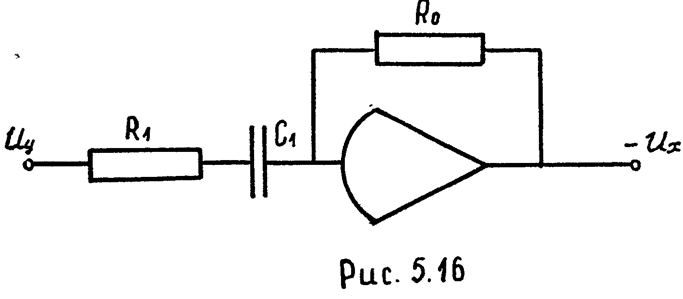
2) Схема модели дифференцирующего звена. Машинная передаточная функция (см. уравнение 5.7)
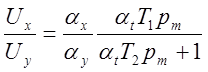 .
.
Из табл. 2 берем цепи №4 и 1 и их сопротивления
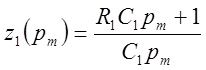 ;
; ![]() .
.
Следовательно,
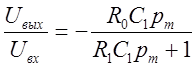 .
.
Очевидно:
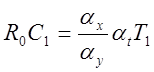 ;
;
![]() .
.
Схема модели дифференцирующего звена изображена на рис, 5.16.
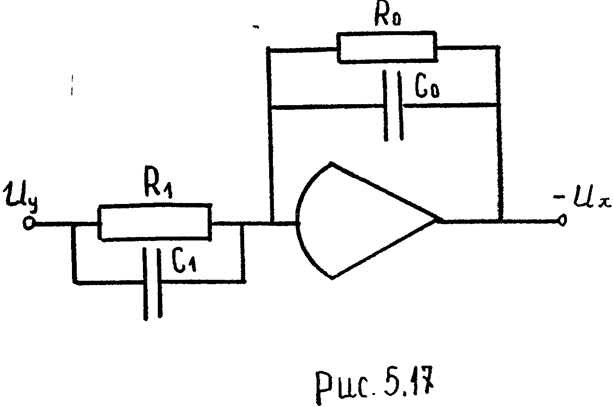
3) Схема модели интегро-дифференцирующего звена. Машинная передаточная функция (см. уравнение 5.8)
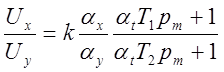 ;
;
а) из табл. 2 (см. разд. 1) берем цепи № 3 и их сопротивления
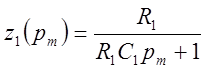 ;
; 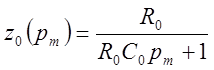 .
.
Следовательно,
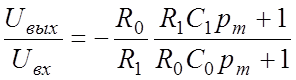 ,
, ![]() .
.
Очевидно,
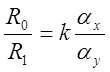 ;
; ![]() ;
; ![]() .
.
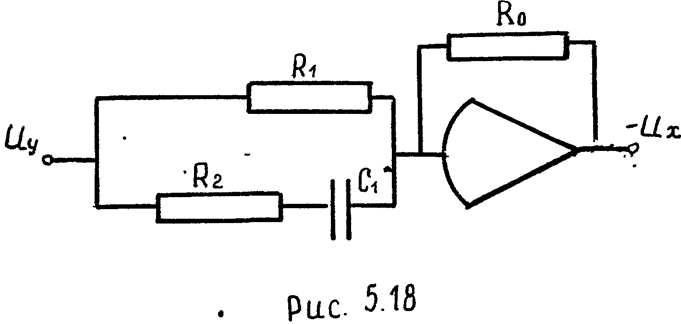
б) Из табл. 2 берем цепи №7б, №1 и их сопротивления
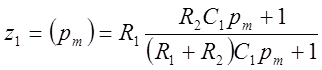 ;
; ![]() ;
; ![]() .
.
Следовательно;
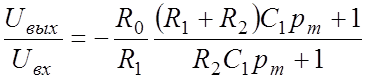 .
.
Очевидно,
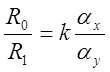 ;
; ![]() ;
;
![]() , причем
, причем ![]() .
.
Схемы моделей интегро-дифференцирующего звена изображены на рис. 5.17 и 5.18.
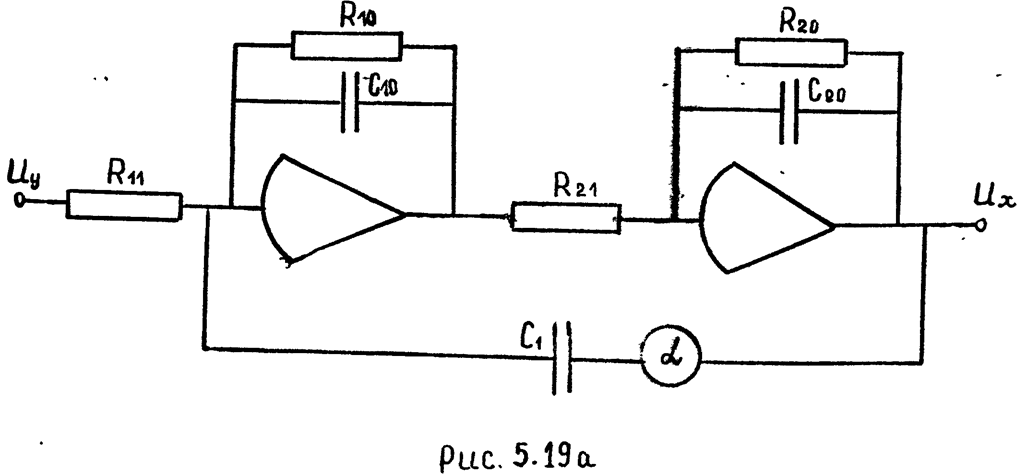
4) Схемы моделей колебательного звена (рис. 5.19 и 5.19а).
Машинная передаточная функция (см. уравнение (5.9))
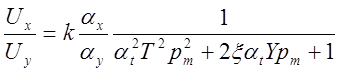 .
.
Для этой схемы
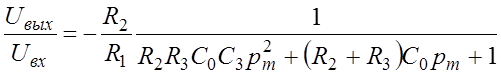 .
.
Очевидно,
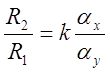 ;
; ![]() ;
; ![]() .
.
Для этой схемы:
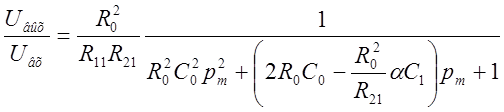 .
.
Очевидно,
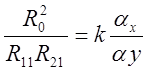 ;
; ![]() ;
; 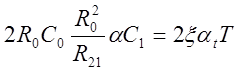 ;
;
или:
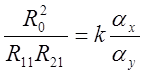 ;
; ![]() ;
; 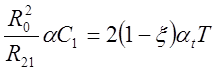 ,
,
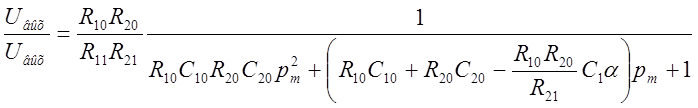 .
.
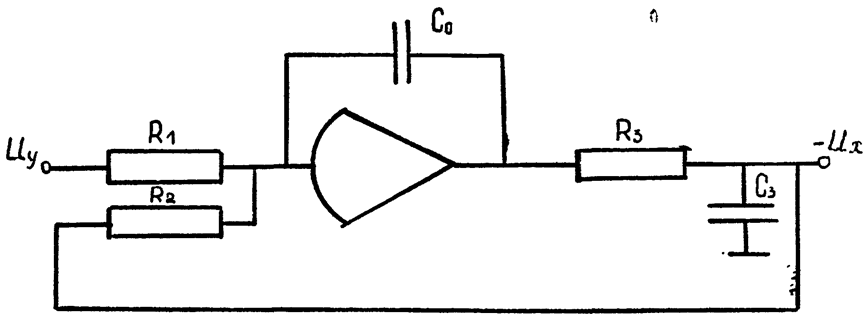
5) Схема модели звена, передаточная функция которого описывается уравнением (5.10)
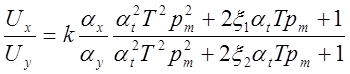 .
.
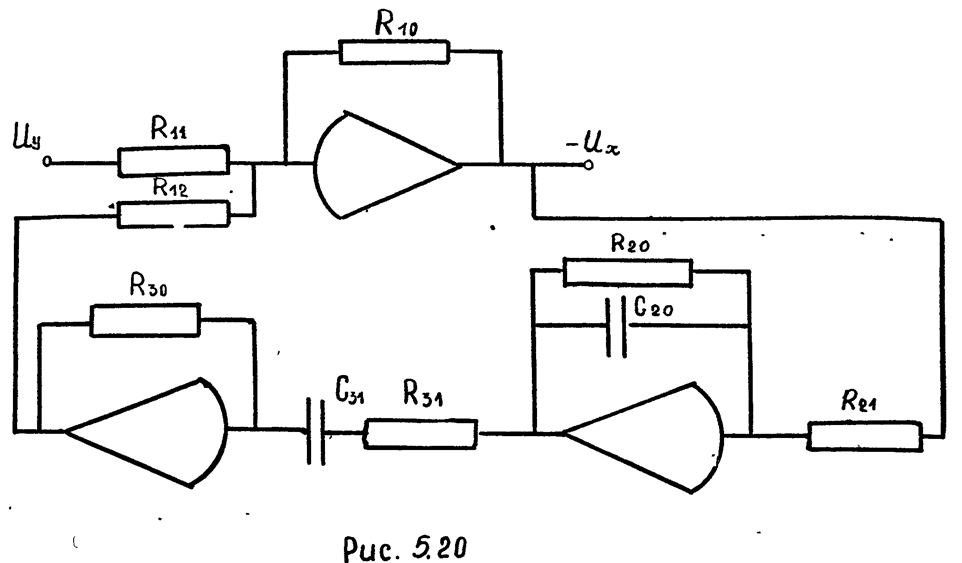
Схема модели рассматриваемого звена, составленная в соответствии с уравнением (5.10а), изображена на рис, 5.20. Очевидно,
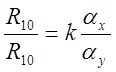 ;
; ![]() ;
;
![]() ;
; 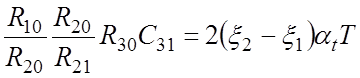 .
.
Рассмотрим числовые примеры определения параметров
моделей звена.
Пример
№ I. Определить параметры модели дифференцирующего звена, если ![]() ,
, ![]() ,
,
![]() .
.
1) Выбираем масштабы:
![]()
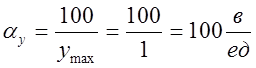
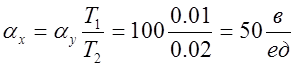
2) Схема модели звена изображена на рис. 5.9.
3) Определяем параметры модели:
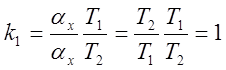 ;
; 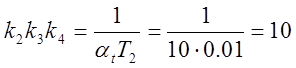 ;
;
задаем ![]() ,
, ![]() ,
тогда
,
тогда ![]() .
.
4) Определяем возмещение в напряжении:
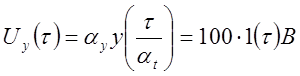
Пример № 2, Определить параметры модели интегро-дифференцирующего звена, если k=5, T1=0.02с.
1) Выбираем масштабы:
![]() ;
; 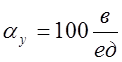 ;
; 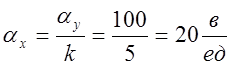 .
.
2) Схема модели звена изображена на рис. 5.10
3) Определяем параметры модели:
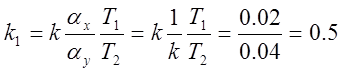 ;
; 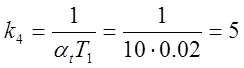 ;
; 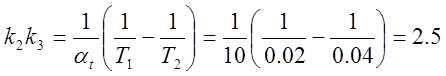 ;
;
задаем k3=1, тогда k2=2.5.
4) Определяем возмущение в напряжении:
![]()
Пример №3. Определить параметры модели колебательного звена, если k=5, T=0.01c, x=0.2, y(t)=1(t).
1) Выбираем масштабы:
![]()
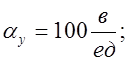
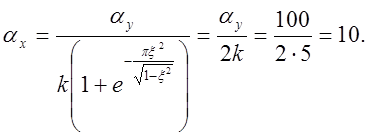
2) Схема модели звена изображена на рис. 5.19а
3) Определяем параметры модели:
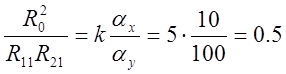 ;
;
![]() ;
;
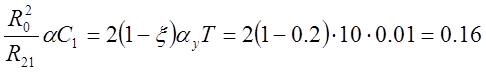 .
.
задаем С0=1мкФ, R11=1мОм, С1=0.5мкФ, тогда R0=0.1мОм, тогда R21=0.02мОм, a=0.64.
4) Определяем возмущение в напряжении:
![]()
Пример №4, Определить параметры модели звена, передаточная функция которого
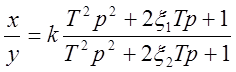 ,
,
если k=5, T=0.1c, x1=2, x2=6, y(t)=1(t).
1) Выбираем масштабы:
![]() ;
;
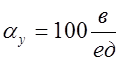 ;
; 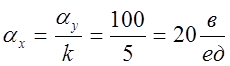 .
.
2) Схема модели звена изображена на рис. 5.20.
3) Определяем параметры модели:
![]()
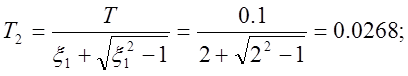
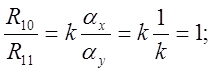
![]()
![]()
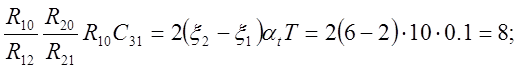
задаем C20=1мкФ, R10=1мОм, С31=0.5мкФ, R21=3.73мОм, R12=0.125мОм, тогда R20=3.73мОм, R11=1МОм, R31=0.536МОм, R30=2МОм
4) Определяем возмущение в напряжении
![]()
Лекция №32
План лекции
1. Составление схем моделирования на основе схем моделей динамических звеньев.
2. Пример составления схем моделирования динамической системы.
5.4. Составление схем моделирования по структурным схемам динамических систем.
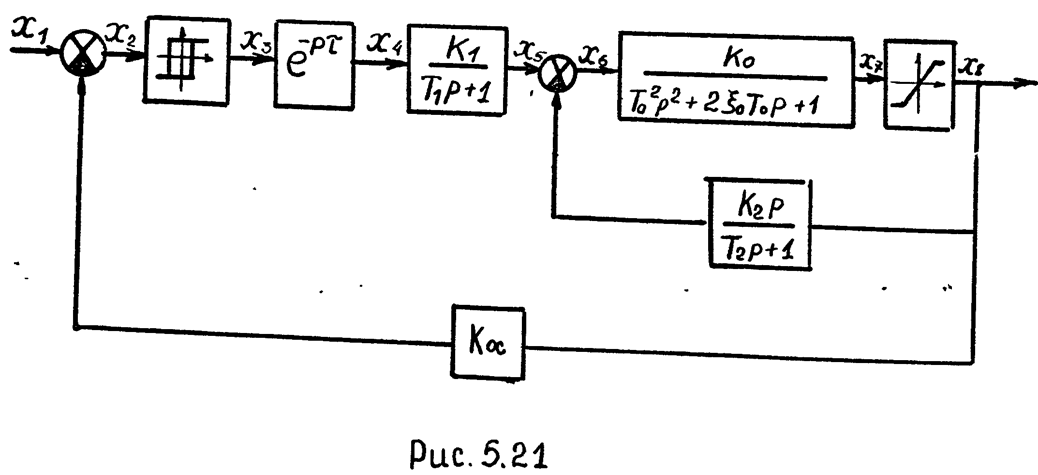
Для составления схемы моделирования динамической системы по структурной схеме необходимо соединить схемы моделей звеньев в соответствии с заданной структурной схемой системы.
В качестве примера составим схемы моделей динамической системы, структурная схема которой изображена на рис. 5.21. Схемы моделей изображены на рис. 5.22 и 5.23.
Если структурная схема динамической системы содержит дифференцирующие и форсирующие динамические звенья, моделирование которых потребует использования дифференцирующего усилителя, то необходимо воспользоваться некоторыми практическими рекомендациями, позволяющими исключить его использование в связи с повышенной чувствительностью к помехам.
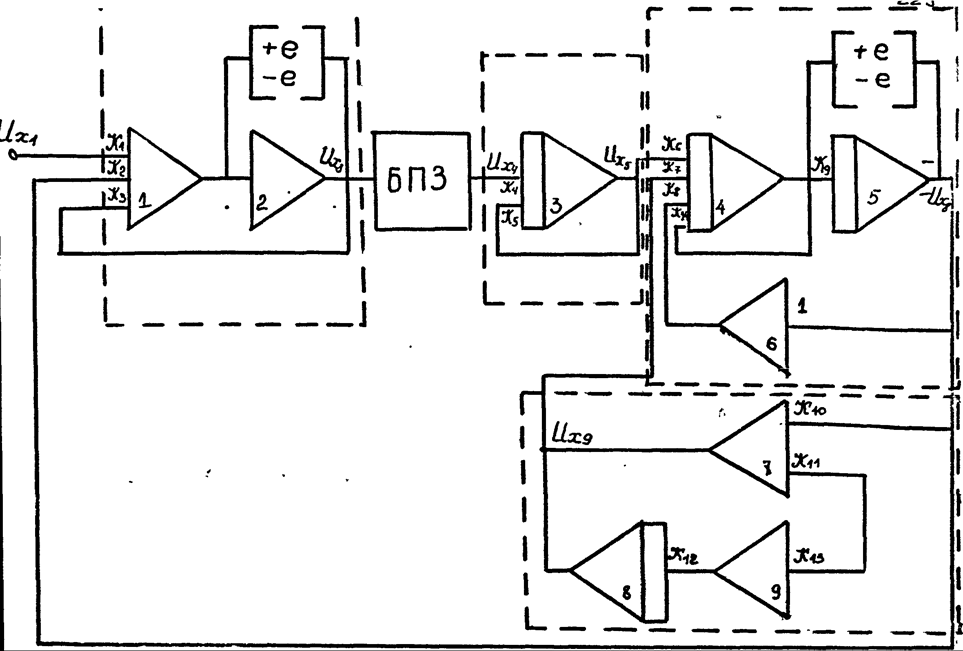
Рис.5.22
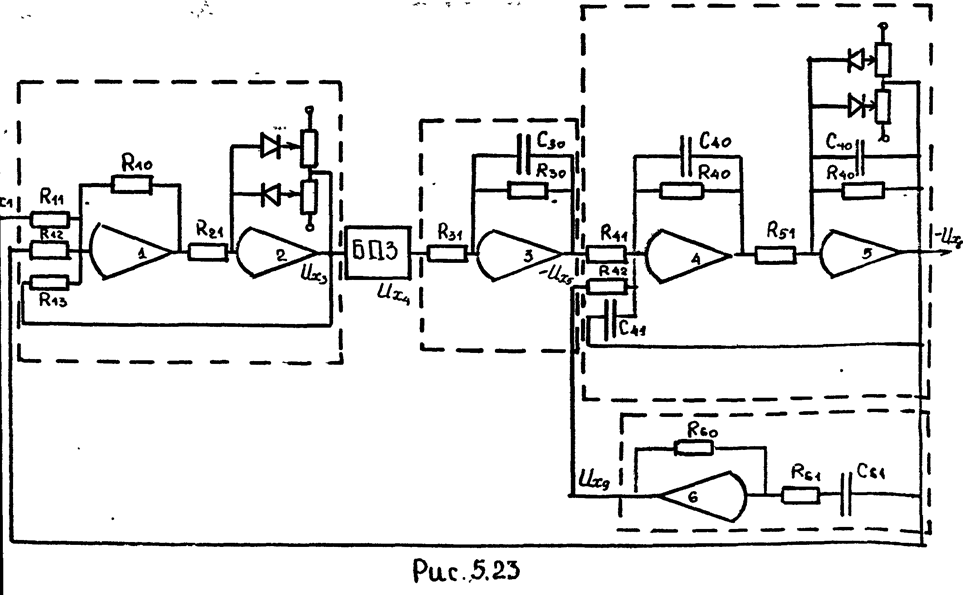
Так, при составлении схемы модели необходимо по возможности объединять дифференцирующие и форсирующие звенья с последующими инерционными звеньями. Тогда при совместном их моделировании на одном решающем усилителе перераспределением значений параметров цепи обратной связи и входной цепи РУ можно ослабить чувствительность усилителя к помехам. Следует отметить, что выполнение такой рекомендации возможно только при использовании схем моделей динамических звеньев на РУ с RC-цепями во входной цепи и цепи обратной связи.
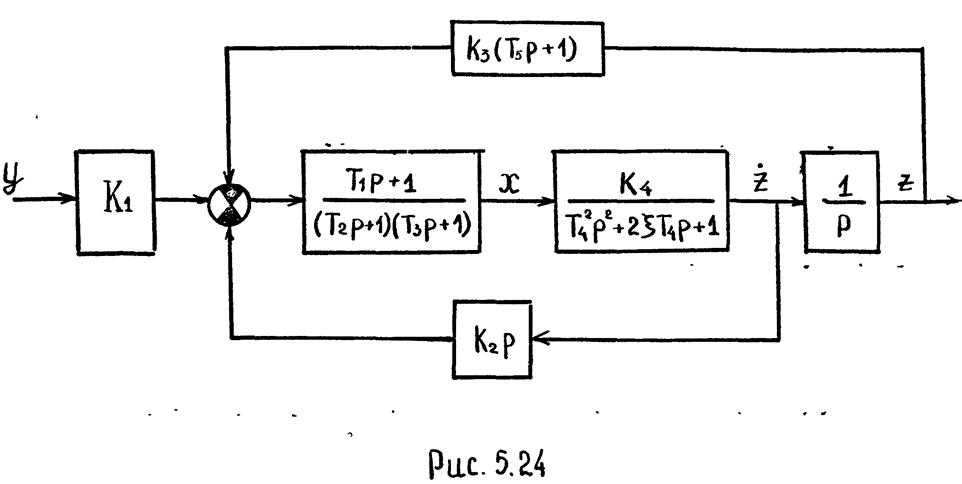
Пусть имеем структурную
схему динамической системы (см. рис. 5.24), содержащую дифференциальное звено k2p
и форсирующее звено k3(T5p+1).
Объединим эти звенья с последующим звеном, имеющим передаточную функцию
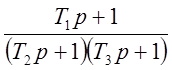 . Для
этого по структурной схеме найдем сигнал x
через
сигналы
. Для
этого по структурной схеме найдем сигнал x
через
сигналы ![]() ,
, ![]() ,
и
,
и ![]()
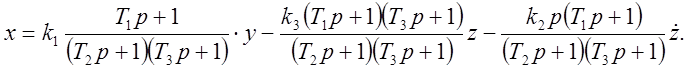
В машинных переменных это уравнение примет вид:
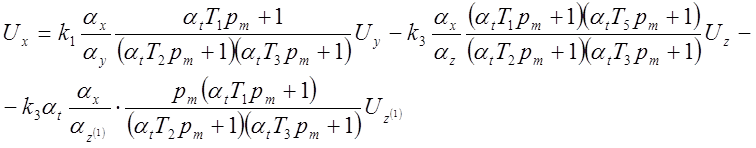 (5.11)
(5.11)
Составим схему модели этой части структурной схемы на одном РУ с RC-цепями, используя понятие передаточной функции РУ по i-тому входу.
Пользуясь
табл. схем RC-цепей, необходимо
подобрать такие схемы RС-цепей
в обратную связь и во входные цепи РУ, чтобы общая часть трех машинных
передаточных функций 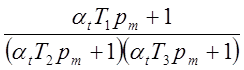 была реализована за счет
комплексного сопротивления RC-цепи
обратной связи РУ, а отличительные их части - за счет комплексных сопротивлений
входных RC-цепей. Из табл. берем
цепи №17а, №1, №2 и №3.
была реализована за счет
комплексного сопротивления RC-цепи
обратной связи РУ, а отличительные их части - за счет комплексных сопротивлений
входных RC-цепей. Из табл. берем
цепи №17а, №1, №2 и №3.
Для них:
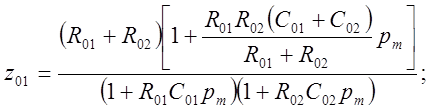
![]()
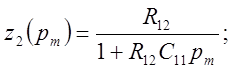
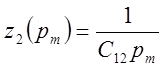
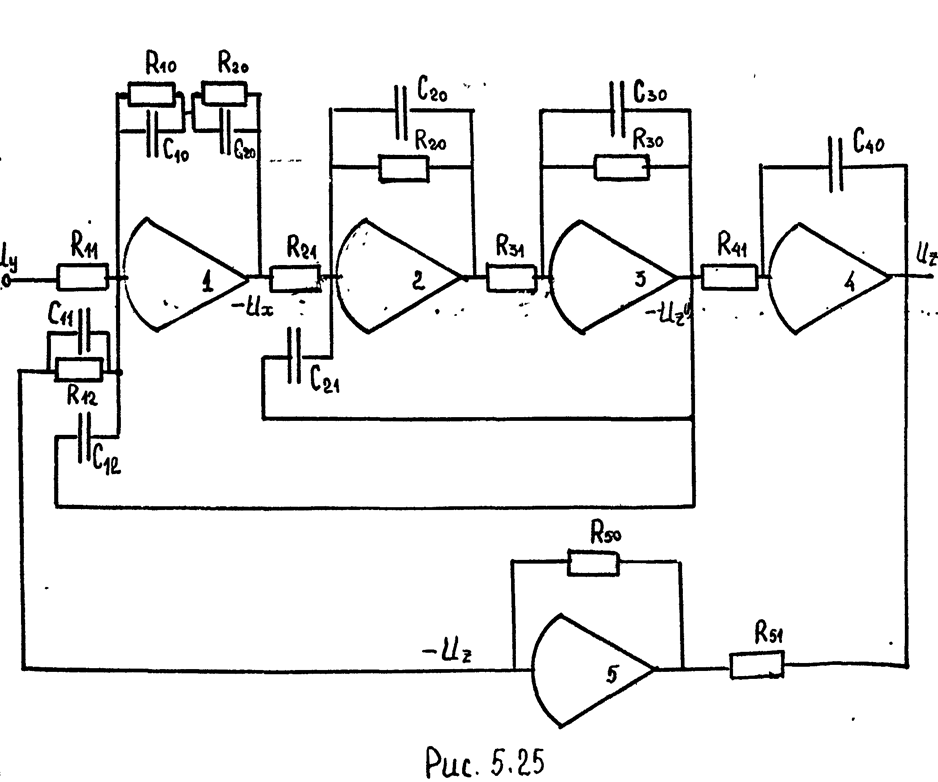
Схема модели динамической системы имеет вид (см. рис. 5.25), для которой запишем сигнал Ux через Uy, Uz, и Uz(1).
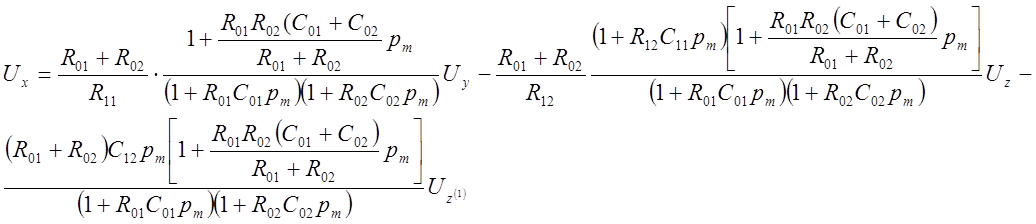 Сопоставляя (5.12) с
(5.11), находим соотношения для расчета
RC-параметров
схемы модели:
Сопоставляя (5.12) с
(5.11), находим соотношения для расчета
RC-параметров
схемы модели:
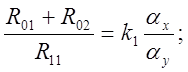
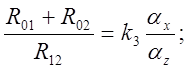
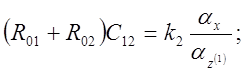
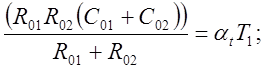
![]()
![]()
![]()
Чтобы
получить работоспособною схему модели, при расчете RC-параметров
необходимо выполнить условие: ![]() и
и ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.