В качестве примера получим соотношения между коэффициентами передачи решающих усилителей, масштабами преобразования переменных и коэффициентами исходного уравнения для модели, структурная схема которой изображена на рис. 4.1.
По структурной схеме для каждого решающего усилителя составляем уравнение, связывающее выходное и входные напряжения:
(№ 7) ![]() (4.12)
(4.12)
(№ 1) 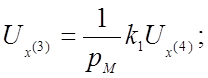
(№ 2) 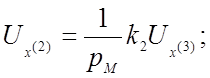
(№ 3) 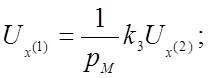
(№ 4) 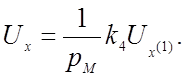
 Из уравнения (4.12)
исключаем напряжения, соответствующие производным:
Из уравнения (4.12)
исключаем напряжения, соответствующие производным:
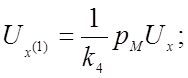
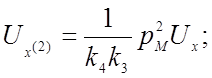
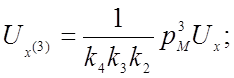 (4.13)
(4.13)
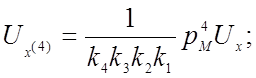
![]() (4.14)
(4.14)
Заменяем в уравнении (4.14) машинные переменные
исходными
переменными, используя уравнения преобразования (4.1) и (4.2): 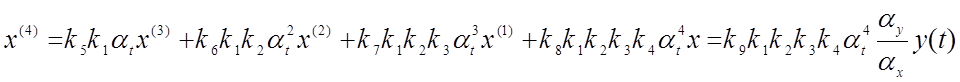
Сопоставляя полученное уравнение с исходным уравнением (4.7), получаем соотношения между коэффициентами передачи решающих усилителей, масштабами преобразований переменных и коэффициентами исходного уравнения:
![]()
![]()
![]() ;
;
![]() (4.15)
(4.15)
![]()
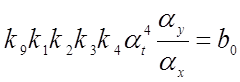
Анализируя уравнения (4.15), структурную схему (рис. 4.1) и исходное уравнение (4.7), можно сформулировать следующие правила, позволяющие получить соотношения между коэффициентами исходного уравнения, коэффициентами передачи решающих элементов и масштабами преобразования переменных:
1) коэффициент исходного уравнения при зависимой переменной или её производной равен произведению коэффициентов передачи решающих элементов, входящих в замкнутый контур, на выходе которого получается соответствующее напряжение, умноженному на масштаб преобразования времени в степени, равной числу интегрирующих усилителей в этом контуре.
2) коэффициент исходного уравнения при независимой переменной (при внешнем возмущении) равен произведению коэффициентов передачи решающих элементов, последовательно включенных в цепь между точкой приложения независимой переменной и выходом искомой зависимой переменной, умноженному на масштаб времени в степени, равной числу интегрирующих усилителей в этой цепи, и на отношение масштабов преобразования независимой и искомой зависимой переменных.
Из уравнений (4.15) следует, что их число меньше числа неизвестных, поэтому некоторые коэффициенты передачи можно задать произвольно, учитывая при этом удобство их установки и свойства решающих элементов. После набора модели и пробного решения может выявиться необходимость изменения некоторых коэффициентов передачи. Если выходное напряжение какого-либо решающего элемента превысит 100 В (или получится значительно меньше 10,0 В), то необходимо уменьшить (увеличить) его коэффициенты передачи. Очевидно, в то же число раз необходимо увеличить (уменьшить) коэффициент передачи последующего решающего элемента по тому входу, на который подается рассматриваемое выходное напряжение. После окончательного выбора коэффициентов передачи решающих элементов производится определение масштабов преобразования всех интересующих переменных.
4.5. Определение возмущений и начальных условий в напряжениях.
Для определения возмущений в напряжениях достаточно воспользоваться уравнением преобразования (4.2):
![]() .
(4.16)
.
(4.16)
Если возмущение представляет заданную функцию времени, то
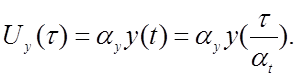 (4.17)
(4.17)
Напряжение
![]() можно воспроизвести путём решения
некоторого вспомогательного уравнения или с помощью вариатора коэффициентов. В
последнем случае напряжение
можно воспроизвести путём решения
некоторого вспомогательного уравнения или с помощью вариатора коэффициентов. В
последнем случае напряжение ![]() целесообразно
представить в виде уравнения
целесообразно
представить в виде уравнения
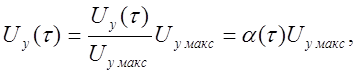 (4.18)
(4.18)
где
![]() (4.19)
(4.19)
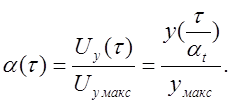 (4.20)
(4.20)
Коэффициент
![]() изменяется от
изменяется от 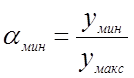 до
до ![]() и
реализуется с помощью вариатора коэффициентов. График
и
реализуется с помощью вариатора коэффициентов. График ![]() получается
из графика
получается
из графика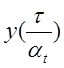 , как показано на рис. 4.4.
, как показано на рис. 4.4.
При определении начальных напряжений могут представиться два случая: 1) масштабы преобразования всех переменных и их производных известны, 2) масштабы преобразования производных неизвестны.
В первом случае для определения начальных напряжений достаточно воспользоваться уравнением преобразования (4.2):
![]() (4.21)
(4.21)
Во втором случае необходимо получить уравнения для определения начальных напряжений, соответствующих производным. Для этого по структурной схеме модели для каждого интегрирующего усилителя (кроме интегрирующего усилителя, на который подается напряжение, соответствующее старшей производной) составляют уравнение, связывающее выходное и входное напряжения.
Используя уравнения (4.13), в качества примера получим уравнения для определения начальных напряжений, соответствующих производным.
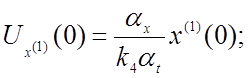
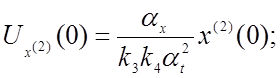 (4.22)
(4.22)
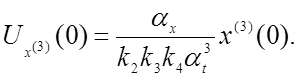
Лекция № 26.
План.
1. Подготовка нелинейного дифференциального уравнения к решению на АВМ.
2. Составление схемы модели.
З. Расчет коэффициентов передач.
4.6. Особенности подготовки нелинейного дифференциального уравнения к решению на АВМ.
Подготовка нелинейного дифференциального уравнения производится, в основном, так же, как и подготовка линейного дифференциального уравнения. При этом в заданном уравнении целесообразно выделить произведения и частные переменных, нелинейные функции и аргументы трансцендентных и неаналитических функций.
Рассмотрим пример подготовки нелинейного дифференциального уравнения. Пусть для решения на АВМ задано нелинейное дифференциальное уравнение 4–го порядка с постоянными коэффициентами:
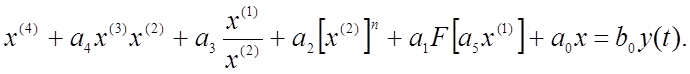 (4.23)
(4.23)
Выделяем в уравнении (4.23) произведение и частное переменных, нелинейные функции и аргумент трансцендентной или неаналитической функции:
![]()
![]()
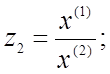
![]()
![]()
![]()
Получаем систему машинных уравнений:
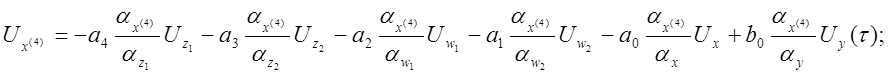
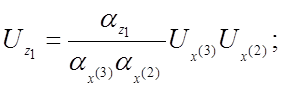
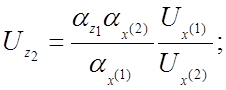
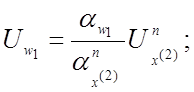
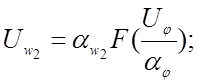
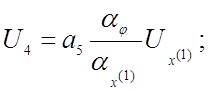
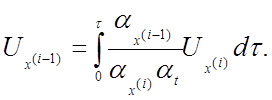
Составляем структурную схему модели (рис. 4.5). Выразим коэффициенты передачи нелинейных решающих элементов через масштабы преобразования переменных.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.