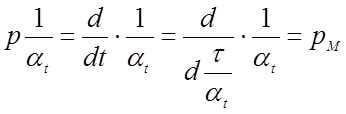Основы математического и физического моделирования систем управления, страница 22

.                                (4.1а)

В качестве зависимой исходной переменной может быть принята любая физическая величина. При моделировании динамических систем в качестве независимой исходной переменной чаще всего принимается время. В этом случае масштаб  называется масштабом преобразования времени или просто масштабом времени. В дальнейшем будем считать, что в качестве независимой исходной переменной принято время.

Если масштаб преобразования времени , процесс в модели должен протекать с той же скоростью, что и в оригинале; если , процесс в модели должен протекать быстрее, при  процесс в модели должен протекать медленнее. Изменение скорости процесса, протекающего в модели, осуществляется изменением коэффициента интегрирующих усилителей, входящих в модель.

При выборе масштаба времени  руководствуются следующими соображениями.

1.  При уменьшении  (увеличении скорости процесса, протекающего в модели) увеличиваются коэффициенты передачи интегрирующих усилителей, вследствие чего возрастают их погрешности, вызываемые напряжением дрейфа  и конечным значением коэффициента усиления . Масштаб времени выбирается с таким расчетом, чтобы коэффициенты передачи интегрирующих усилителей не превышали допустимую величину (5-10).

2.  При увеличении  (уменьшении скорости процесса, протекающего в модели) увеличивается длительность интегрирования, вследствие чего возрастают накопляемые в процессе интегрирования погрешности. Масштаб времени выбирается с таким расчетом, чтобы длительность интегрирования не превышала допустимую величину. Для большинства АВМ допустимая длительность интегрирования лежит в пределах 150 - 2000 сек.

Кроме этих соображений при выборе масштаба времени  необходимо учитывать частотные характеристики решающих элементов и требования удобства наблюдения и регистрации напряжений.

При использовании в модели вариатора коэффициентов с шаговыми искателями масштаб времени должен удовлетворять соотношению

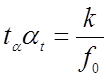
- заданное время изменения коэффициента

k - число равных участков, на которые разбит по оси абсцисс график ,

 - постоянная частота импульсов, подаваемых на вариатор коэффициентов.

При выборе масштаба преобразования следует стремиться к тому, чтобы решение уравнений протекало при наибольшем допустимом уровне напряжений в АВМ, что обеспечивает получение малых погрешностей переменных. Из уравнения (4.2) , полагая , получаем

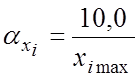
где  - максимальное ожидаемое значение переменной .

Уравнение (4.4) требует определения  до решения заданных уравнений на АВМ хотя бы приближенно, но с запасом  в большую сторону.

Получим соотношение между масштабами преобразования произведения и сомножителей. Если  z =xy, то, принимая во внимание уравнение преобразования (4.2),

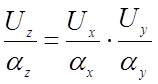, откуда

.

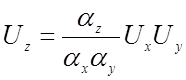Так как для множительного устройства

     ,                     

                                          то 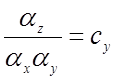                             (4.5)

Получим соотношение между масштабами преобразования частного, делимого и делителя. Если 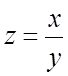 , то, принимая во внимание уранение преобразования (4.2),

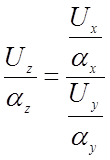, откуда  .

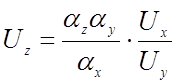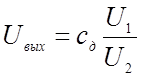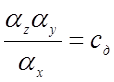Так как для делительного устройства    ,  то      (4.6)
Лекция № 2З

План лекции

1. Методика решения дифференциальных уравнений на АВМ.

2. Получение системы машинных уравнений.

3. Условные обозначения решающих элементов.

4. Составление схемы модели.

4.2. Получение системы машинных уравнений.

Дифференциальные уравнения могут быть решены на АВМ методом понижения или методом повышения порядка производной. В первом случае основу модели должны составлять интегрирующие усилители, а во втором - дифференцирующие усилители. Дифференцирующие усилители обладают повышенной чувствительностью к помехам, поэтому дифференциальные уравнения решаются на АВМ, как правило, методом понижения порядка производной. В этом случае для получения системы машинных уравнений необходимо:

1)заменить в заданных уравнениях исходные переменные машинными переменными, используя уравнения преобразования;

2)разрешить полученные уравнения относительно напряжений, соответствующих старшим производным.

Рассмотрим пример получения системы машинных уравнений. Пусть для решения на АВМ задано линейное дифференциальное уравнение 4-го порядка с постоянными коэффициентами.

                         (4.7)

Заменяем в уравнении (4.7) исходные переменные машинными переменными, используя уравнения преобразования (4.1) и (4.2):

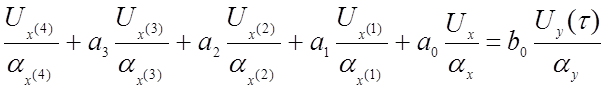,                 (4.7а)

где   .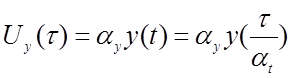

Разрешаем уравнение (4.7а) относительно напряжения :

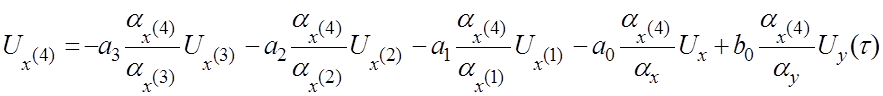 (4.8)

Выразим напряжение 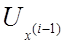 через напряжение

Так как 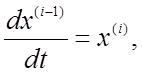 то, принимая во внимание уравнения преобразования (4.1) и (4.2),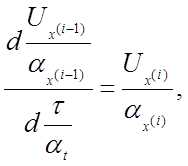                                                          

откуда

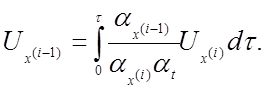                                     (4.9)

Уравнения (4.8) и (4.9) представляют систему машинных уравнений для рассматриваемого примера.

4.3. Составление структурной схемы модели.

Структурная схема модели составляется в соответствии с системой машинных уравнений. В таблице 4.1. приведены условные обозначения решающих элементов, принятые для составления структурных схем и устанавливаемые ГОСТ 23335-78 и ГОСТ 23336-78.

В качестве примера составим структурную схему модели в соответствии с системой машинных уравнений (4.8) и (4.9). Пред­положим, что напряжение  нам известно. Тогда, как показывает уравнение (4.9), напряжения   могут быть получены последовательным интегрированием.  Напряжение , как показывает уравнение (4.8), может быть получено суммированием напряжений , полученных с выходов интегрирующих усилителей, и напряжения , подаваемого извне. При составлении структурной схемы, изображенной на рис. 4.1, принято во внимание свойство решающих усилителей изменять знак входного напряжения.