21.Подчуфаров Ю.Б. Мозжечков В.А. Физическое моделирование систем автоматического регулирования. Учеб. пособие. – Тула, ТулПИ, 1984, 76 с.
Лекция № I ВВОДНАЯ
План
1. Сущность моделирования.
2. Физические и математические модели.
3. Машинное моделирование.
4. АВМ, достоинства, недостатки.
5. АЦВМ - эффективное средство моделирования.
Моделирование как метод получения информации о поведении динамических систем занимает промежуточное место между аналитическими исследованиями и натурным экспериментом.
Моделирование систем управления (СУ) летательными аппаратами в настоящее время является обязательным этапом проектирования, разработки и испытаний. Это обусловлено следующим. Во-первых, в силу исключительной сложности СУ их аналитический расчет возможен только в очень ограниченных пределах, и моделирование является единственным средством анализа и синтеза. Во-вторых, оно позволяет проводить и оценить результаты, получаемые в реальных условиях, путем многократной проверки на модели с включением реальной аппаратуры.
Моделирование заключается в замене исходных систем или явлений (оригиналов) другими системами или явлениями, называемыми моделями, которые в той или иной мере воспроизводят свойства оригинала.
Из возможных видов моделей выделим физические и математические модели, которые воспроизводят процессы, протекающие в оригинале, и предназначены для исследования этих процессов с меньшими затратами средств и времени.
Физические модели имеют одинаковую с оригиналом физическую природу и отличаются от него размерами и мощностью. Построение физических моделей основано на правилах теории подобия. Физическая модель воспроизводит все стороны процесса, протекающего в оригинале, в том числе и такие его стороны, которые не поддаются математическому описанию, но физическая модель мало универсальна.
Примеры физических моделей: модели ракет в аэродинамических трубах, модели судов в "опытовых" бассейнах и др.
Математические модели имеют отличную от оригинала физическую природу и эквиваленты ему по математическому описанию. Построение математических моделей основано на идентичности уравнений описывающих процессы различной физической природы. В.И. Ленин в работе "Материализм и эмпириокритицизм" писал: "Единство природы обнаруживается в "поразительной аналогичности" дифференциальных уравнений, относящихся к разным областям явлений".
Самые разнообразные явления описываются одними и теми же уравнениями, и в этом проявляется универсальность математических моделей. Математическая модель воспроизводит только те стороны процесса, которые были отражены в уравнениях, описывающих процесс, но она обладает универсальностью.
Одним из способов математического моделирования является машинное моделирование, когда модель строится из отдельных решающих элементов, выполняющих определенные математические операции. Соединение решающих элементов осуществляется в соответствии с уравнениями, описывающими процесс в оригинале.
Рассмотрим пример. Движение механической системы, приведенной на рис. I., описывается уравнением (1).
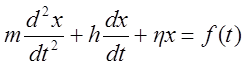(1)
Структурная схема математической машинной модели, составленная в соответствии с уравнением (I), предварительно представленном в виде
,
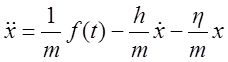(1a)
приведена на рис. 2.
На
схеме знаком интеграла обозначены интегрирующие элементы, знаком суммы -
суммирующий элемент, знаком Кi – элементы, выполняющие умножение на
постоянный коэффициент. На вход первого интегрирующего элемента поступает величина
. Полученные на
выходах интегрирующих элементов величины 
и x и изменяющаяся по заданному закону
величина f(t)в соответствии с уравнением (1а) умножаются на постоянные
коэффициенты и складываются суммирующим элементом. На выходе суммирующего
элемента получается величина , которая и подается на вход первого
интегрирующего элемента, замыкая тем самым схему модели.
Мощным средством построения математических моделей являются вычислительные машины. Используя вычислительные машины для решения дифференциальных уравнений, описывающих изучаемый процесс, можно с помощью универсального инструмента воспроизводить процессы, аналогичные различным физическим явлениям, легко осуществлять разнообразные вычислительные (модельные) эксперименты. Именно эта универсальность и удобство выполнение разнообразных вариаций и обусловили широкое распространение
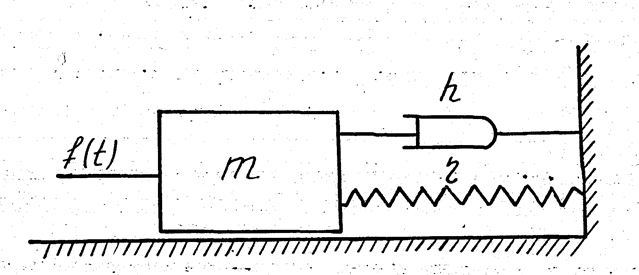
Рис. 1
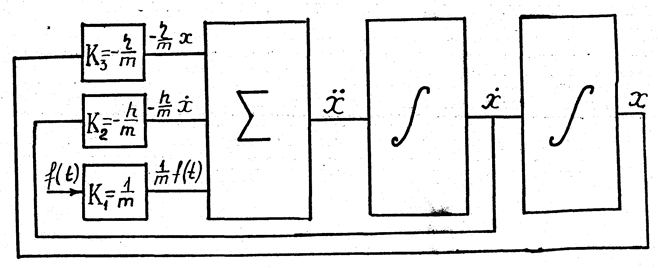
Рис. 2
метода математического моделирования. При машинном моделировании исходным переменным ставятся в соответствие машинные переменные. Ими могут быть электрические напряжения, как это имеет место в аналоговых вычислительных машинах и системах (АВМ и АВС), или кодовые комбинации, как это имеет место в цифровых вычислительных машинах (ЦВМ).
В зависимости от используемых вычислительных машин различают моделирование на АВМ, ЦВМ и аналого-цифровое, когда в системе моделирования одновременно используются АВМ и ЦВМ, образуя АЦВМ и АЦВС. При машинном моделировании с вычислительной системой может сопрягаться реальная аппаратура. Это - полунатурное моделирование, позволяющее воспроизводить процессы, которые частично не имеют математического описания.
Для исследования САУ аналоговое моделирование во многих случаях является более предпочтительным, чем цифровое. Как правило, работа САУ описывается дифференциальными уравнениями, для решения которых и предназначены АВМ. Кроме того, свойство "грубости" САУ позволяет получать удовлетворительные оценки качества управления при ограниченной точности элементов АВМ.
В настоящее время, несмотря на значительные успехи в области моделирования САУ на ЦВМ, аналоговое моделирование продолжает оставаться мощным средством изучения САУ.
Серийное изготовление АВМ в нашей стране началось с 1946 г. С тех пор было разработано и изготовлено большое число ламповых АВМ (ИПТ-5, МПТ-9, ЛМУ-1, ЭМУ-10, МН-7, MH-I4, MH-I7 и др.). Вместе с первым поколением ламповых АВМ в конце 50-х годов, когда развилась полупроводниковая техника, стали выпускать АВМ на полупроводниках - АВМ второго поколения (MH-10M, МH-I8, АВК-2 и др.).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.