Основы математического и физического моделирования систем управления, страница 26

Выражаем коэффициенты передачи интегрирующих усилителей через коэффициенты исходного уравнения и масштабы преобразования переменных, пользуясь сформулированными в 4.1 правилами: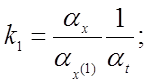  

 

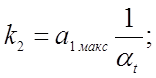
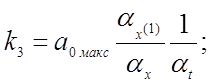
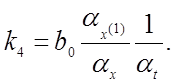
Получаем соотношения между коэффициентами исходного урав­нения, коэффициентами передачи решающих элементов и масштабами преобразования переменных, пользуясь сформулированными правилами:

  

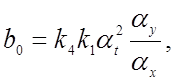
откуда

  

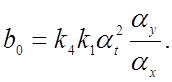
4.8. Особенности подготовки системы уравнений к решению на АВМ.

       Подготовка каждого уравнения, входящего в систему, производится так же, как и одного заданного уравнения. При этом переменную  и её производные, входящие в i –тое уравнение, можно рассматривать как внешние возмущения по отношению к переменной x_i.

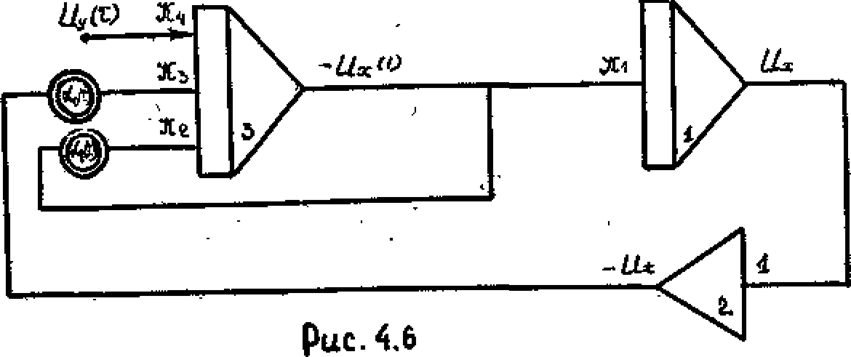
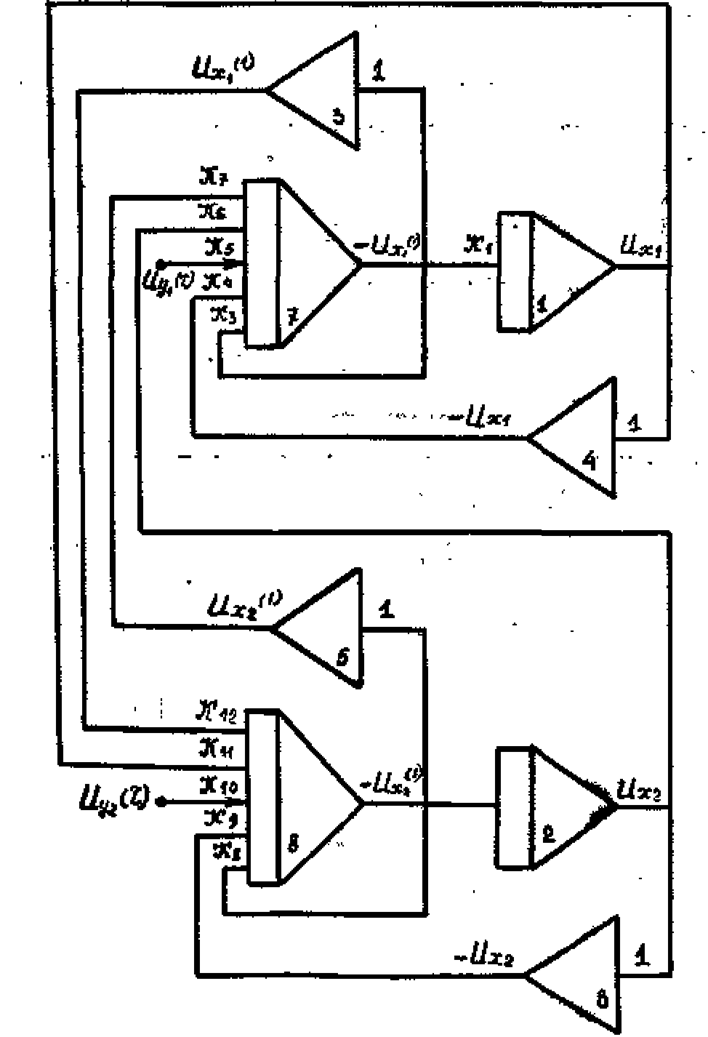
Рис. 4.7

Рассмотрим пример подготовки системы уравнений. Пусть для решения на АВМ задана система двух линейных дифференциальных уравнений 2-го порядка с постоянными коэффициентами:

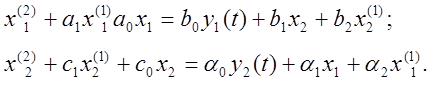                             (4.30)

Получаем систему машинных уравнений:

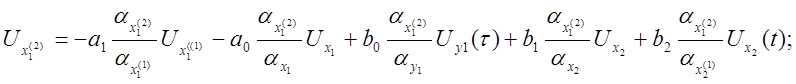
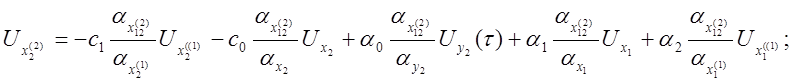
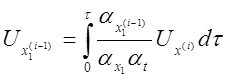
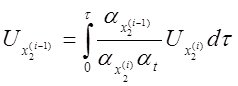
Составляем структурную схему модели (рис. 4.7)

Получаем соотношения между коэффициентами исходных уравнений, коэффициентами передачи интегрирующих усилителей и масштабами преобразования переменных, пользуясь сформулированными правилами:

    

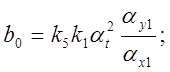
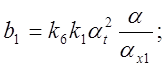
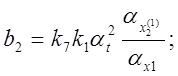
Лекция №28.

План лекции

1.         Пример №1

2.         Пример №2

3.         Пример .№3

4.         Пример №4

5.         Пример № 5

4.9. Примеры подготовки уравнений к решению наАВМ.

Пример № I. Подготовить к решению на АВМ уравнение движения тела (рис .4.8).

при следующих исходных данных:

масса тела – m=50×10^-3 кГсек²/см;

усилие предварительного поджатия пружины – Р₀=0;

жесткость пружины - h=500 кг/см;

коэффициент вязкого трения – h=0.5 кГсек/см;

начальное перемещение – x(0)=0;

начальная скорость – x’(0)=200 см/сек.

1) Для выбора масштабов преобразования переменных определим период, амплитуду и максимальное ускорение для случая незатухающих колебаний (h=0):

   

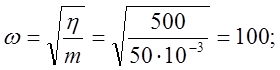
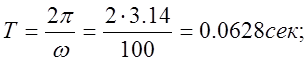
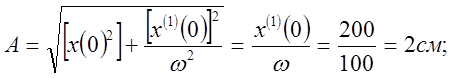
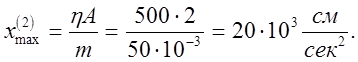
Выбираем масштабы:    

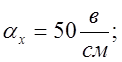
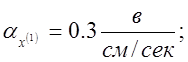
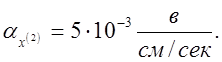
2) Получаем систему машинных уравнений:

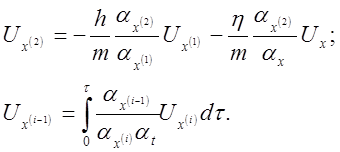
3) Составляем структурную схему модели (рис. 9)

4) Определяем коэффициенты передачи решающих усилителей:

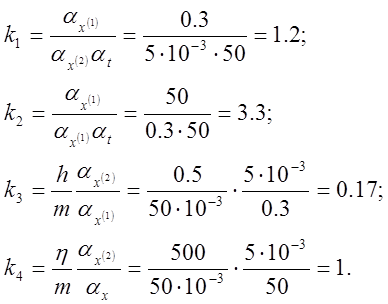
5) определяем начальные напряжения:

 

Пример№2. Подготовить к решению на АВМ уравнение:

при возмущении y(t)=20 и начальных условиях: х(0)=20, х⁽¹⁾(0)=300, х⁽²⁾(0)=4×10³.

1)  Выбираем масштабы:  , .

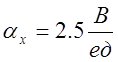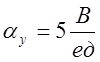2)  Получаем систему машинных уравнений:

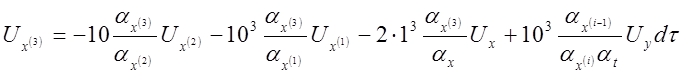
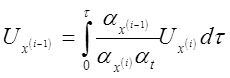
3)  Составляем структурную схему модели (рис.4.10).

4)  Определяем коэффициенты передачи интегрирующих усилителей: ; ; ; .

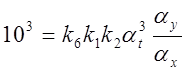Откуда: ; ; ;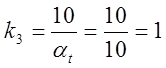

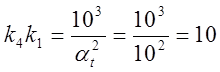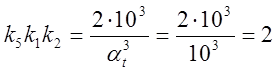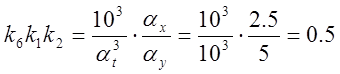
Задаем k₁=1, k₂=1, тогда k₄=10, k₅=2, k₆=0.5.

5)  Определяем возмущение и начальные напряжения:

;

;

;

.

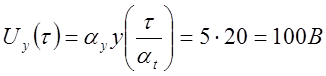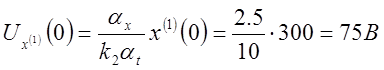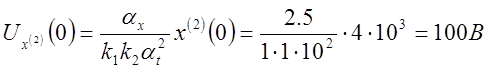Пример №3. Подготовить к решению на АВМ уравнение:

при начальных условиях:   

1)  Выделяем в заданном уравнении произведение переменных и нелинейную функцию:

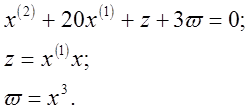
2)  Выбираем масштабы   

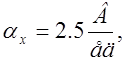
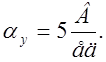
3)  Получаем систему машинных уравнений:

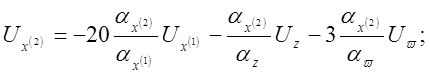
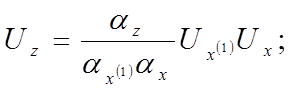
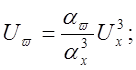
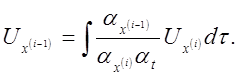
4)  Составляем структурную схему модели (рис 4.11).

5)  Определяем коэффициенты передачи решающих элементов:

         

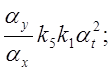
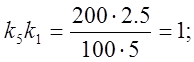
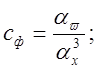
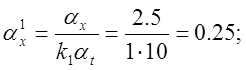
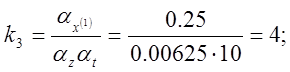
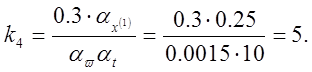
6)  Определяем начальные напряжения:

 

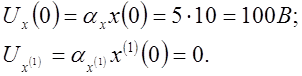
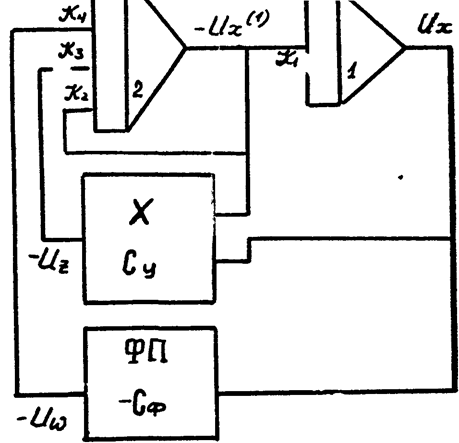
рис. 4.11

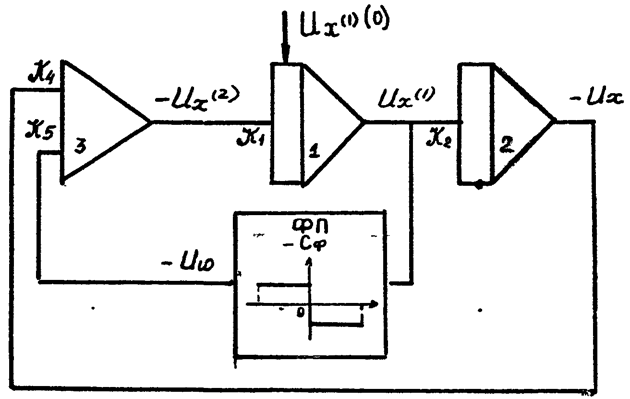
рис. 4.12

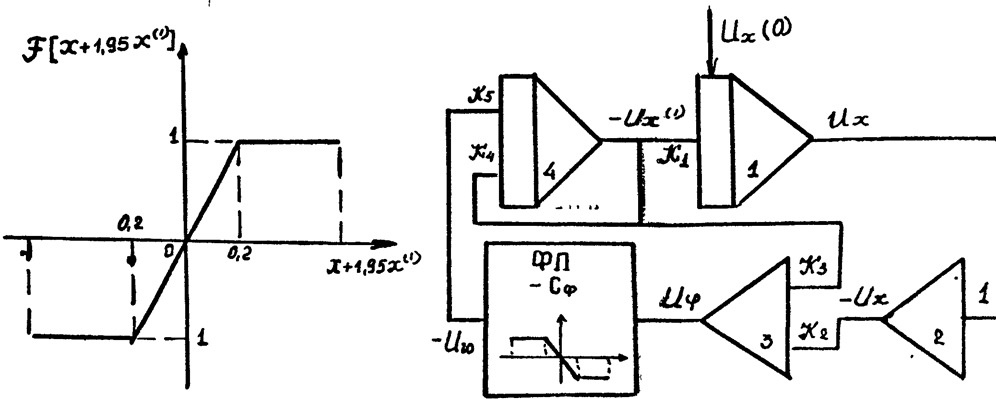
рис. 4.13                                                                     рис.4.14

Пример №4. Подготовить к решению на АВМ уравнение:

;

при начальных условиях: х(0)=0; х⁽¹⁾(0)=200.

1)  Выделяем в заданном уравнении нелинейную функцию:

;

.

2)  Выбираем масштабы:  .

3)  Получаем систему машинных уравнений:

;

;

.

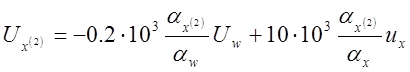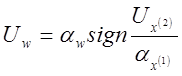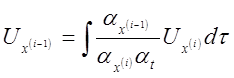4)  составляем структурную схему модели (рис 4.12).

5)  Определяем коэффициенты передачи решающих элементов:

; ; ; ;

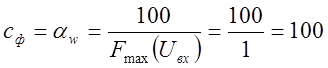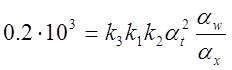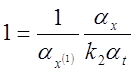откуда: ; ; ;

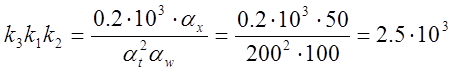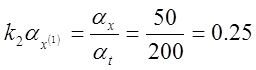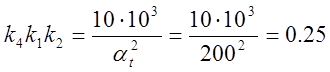задаем k₁=0.5; k₂=0.5, тогда k₃=0.01; k₄=1; a_x⁽¹⁾=0.5

6)  Определяем начальные напряжения:

;

Пример №5. Подготовить к решению на АВМ уравнение

при начальных условиях  . Функция задана графиком (рис. 4.13).

1)  Выделяем в заданном уравнении нелинейную функцию и ее аргумент:

  

2)  Выбираем масштабы   

3)  Получаем систему машинных уравнении:

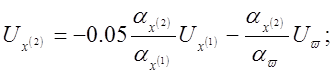
4)  Составляем структурную схему модели (рис. 4.14).

5)  Определяем коэффициенты передачи решающих элементов:

   

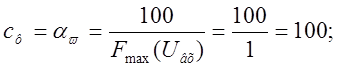
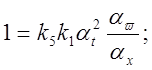
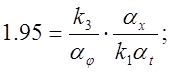
откуда:    

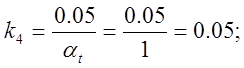
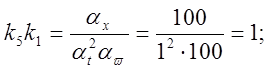
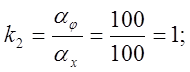
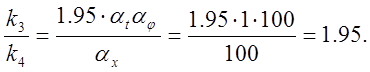
Задаем k₁=1, тогда k₅=1, k₃=1.95.

6) Определяем начальные напряжения:

Лекция №29

План

1. Структурное моделирование.

2. Учет переходной и амплитудной частотной характеристик звена при выборе масштабов преобразования.

 3. Получение машинной передаточной функции звена.

ВЫПОЛНЕНИЕ ПОДГОТОВИТЕЛЬНЫХ ОПЕРАЦИЙ ПРИ МОДЕЛИРОВАНИИ ДИНАМИЧЕСКОЙ СИСТЕМЫ ПО ЕЁ СТРУКТУРНОЙ СХЕМЕ.

Наиболее распространенным видом математического описания САУ, используемым в современной теории и практике управления, является описание в форме структурных схем. Применение структурных схем для описания систем управления и развития методика структурных преобразований послужили основанием для широкого использования структурного моделирования САУ,

Суть структурного моделирования заключается в том, что формирование схемы моделирования исследуемой системы осуществляется по динамическим звеньям и связям, заданным структурной схемой системы.

Моделирование динамической системы по её структурной схеме осуществляется так, что каждое звено структурной схемы динамической системы моделируется соответствующим звеном математической модели. В этом случае подготовительные операции, перечисленные в главе 1, выполняются для каждого звена структурной схемы динамической системы и имеют определенную специфику. После выполнения этих операций составляется структурная схема модели динамической системы, для чего схемы моделей звеньев соединяются в соответствии с заданной структурной схемой динамической системы.

5.1. УЧЁТ ПЕРЕХОДНОЙ И АМПЛИТУДНОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИК ЗВЕНА ПРИ ВЫБОРЕ МАСШТАБОВ ПРЕ­БРАЗОВАНИЯ ПЕРЕМЕННЫХ