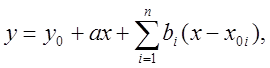 (2.1)
(2.1)
![]() 0 при x£x0i
0 при x£x0i
где bi=
bi=const при x>x0i
Физические переменные x и y при моделировании заменяются машинными переменными - напряжениями UX и UY или Uвх и Uвых, т.е.
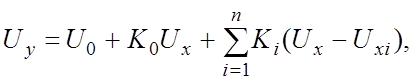
![]() 0
при UX£UXi
0
при UX£UXi
где Ki=
Ki при UX > UXi
Первым слагаемым является постоянное напряжение U0. Второе слагаемое представляет собой сигнал, пропорциональный входному напряжению, т.е. результат обычного линейного преобразования напряжения.
Рассмотрим схемы нелинейных звеньев для получения слагаемых, пропорциональных разности входного сигнала и заданного начального сигнала, т.е. воспроизведение ломанных линий. Схемы звеньев построены на диодах, которые запираются или отпираются входным напряжением.
2.2. Воспроизведение ломаных линий с помощью решающего усилителя.
1. Решающий усилитель с диодом во входной цепи.
На рис. 2.1а изображена схема решающего усилителя, у которого во входную цепь включен диод D. Величиной "+Е " обозначено постоянное положительное опорное напряжение, величиной rg - сопротивление диода.
Токи i1 и i0 определяются выражениями
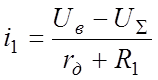 ;
; 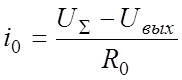 ,
,
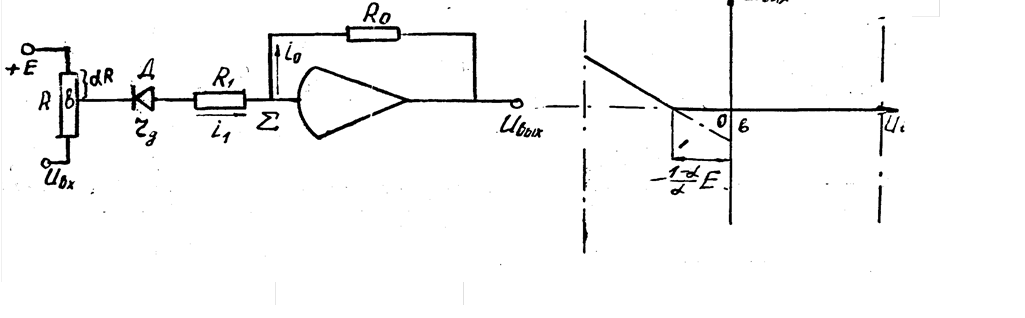 рис. 2.1
рис. 2.1
|
Uвх |
-Uвх |
||
|
|
|||
|
|
|||
рис. 2.2
Согласно уравнению (1.2)
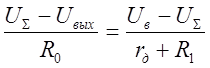 (a)
(a)
Согласно уравнению (1.16)
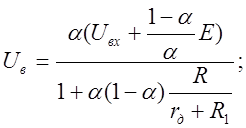 (б)
(б)
Подставляя выражение Uв в уравнение (а) и полагая US=0, имеем
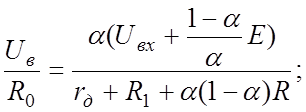 (в)
(в)
При
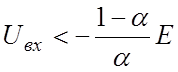 , как показывает уравнение (б),
Uв<0, и диод будет открыт. Когда диод открыт, его сопротивление практически
равно нулю rg
=0. При этом уравнение (в) принимает вид
, как показывает уравнение (б),
Uв<0, и диод будет открыт. Когда диод открыт, его сопротивление практически
равно нулю rg
=0. При этом уравнение (в) принимает вид
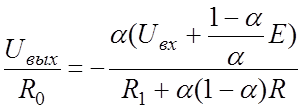 ,
,
откуда
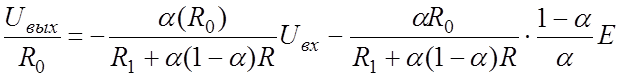
При 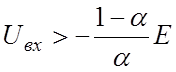 , как показывает
уравнение (б), Uв>0, и диод будет закрыт. Когда диод закрыт, его
сопротивление практически равно бесконечности rg=¥.
, как показывает
уравнение (б), Uв>0, и диод будет закрыт. Когда диод закрыт, его
сопротивление практически равно бесконечности rg=¥.
При этом уравнение (в) принимает вид
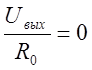 ,
,
откуда
Uвых=0.
Таким образом
![]() -KUвх-b
при
-KUвх-b
при 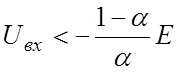
Uвых
= 0 при 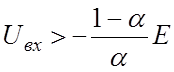
где
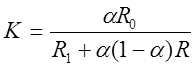 ; (2.3)
; (2.3)
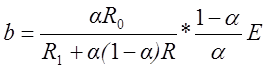 (2.4)
(2.4)
График Uвых=f(Uвх) изображен на рис. 2.1 б.
Изменяя знак опорного напряжения, переключая электроды диода и подавая прямое или инвертированное входное напряжение с помощью решающего усилителя с диодом во входной цепи можно получить восемь типов ломаной линии, изображенных на рис. 2.2
2. Решающий усилитель с диодом в цепи обратной связи.
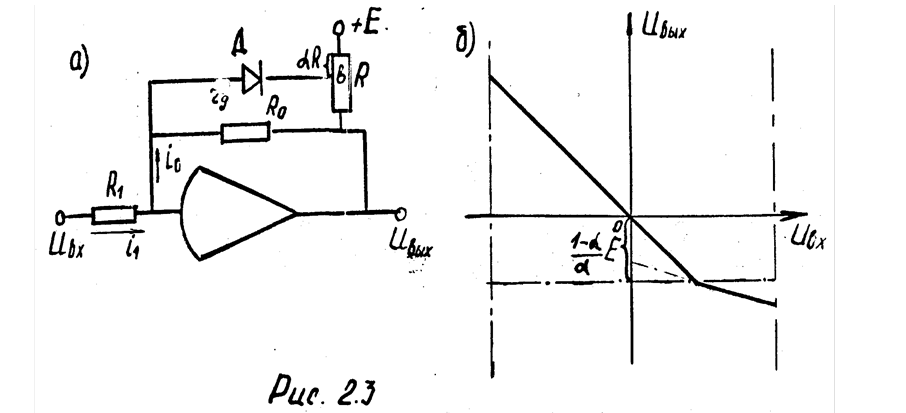
На рис 2.3 а изображена схема решающего усилителя, у которого в цепи обратной связи включен диод D.
Токи i1 и i0 определяются выражениями
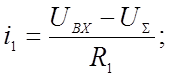
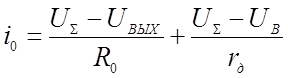
Согласно уравнению (1.2)
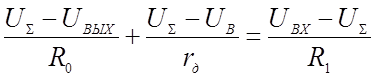 (a)
(a)
Согласно уравнению (1.17)
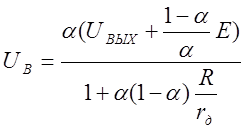 (б)
(б)
Подставляя выражение UВ в уравнение (а) и полагая US = 0, имеем
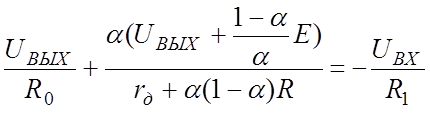
При 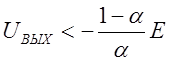 , как показывает
уравнение (б), Uв<0, и диод будет открыт (rg=0).
, как показывает
уравнение (б), Uв<0, и диод будет открыт (rg=0).
При этом уравнение (в) принимает вид
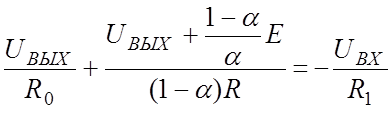
откуда
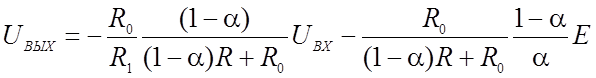
|
Uвх |
-Uвх |
||
|
|
|||
|
|
|||
рис. 2.4
При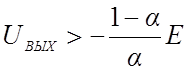 , как показывает уравнение
(б), UВ> 0, и диод будет закрыт ( rg = ¥ ), при этом
уравнение (в) принимает вид
, как показывает уравнение
(б), UВ> 0, и диод будет закрыт ( rg = ¥ ), при этом
уравнение (в) принимает вид
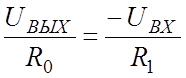 ;
;
откуда
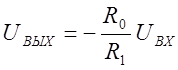
![]() Таким образом,
Таким образом,
-K1UВХ-b1 при 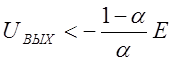 ,
,
UВЫХ -K2UВХ
при 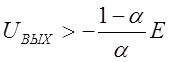 , (2.5)
, (2.5)
где
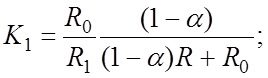 (2.6)
(2.6)
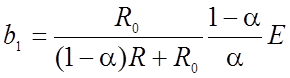 (2.7)
(2.7)
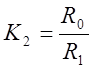 (2.8)
(2.8)
График UВЫХ=f(UВХ) изображен на рис. 2.3 б.
![]() Если R<<R0 и R1,
то K1»0
Если R<<R0 и R1,
то K1»0 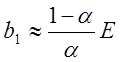 и уравнение (2.4) принимает вид
и уравнение (2.4) принимает вид
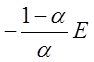 при
при
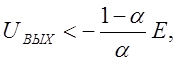
UВЫХ= -KUВХ при 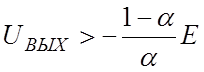 (2.5а)
(2.5а)
График UВЫХ=f(UВХ) для этого случая изображен на рис. 2.3б пунктирной линией.
Изменяя знак опорного напряжения, переключая электроды диода и подавая прямое или инвертированное входное напряжение, с помощью решающего усилителя с диодом в цепи обратной связи можно получить восемь типов ломаной линии, изображенных на рис. 2.4.
Лекция №11
1. Диодный универсальный функциональный преобразователь (ДУФП).
2. Принцип работы.
3. Схема ДУФП.
2.3. Диодный универсальный функциональный преобразователь.
1. Принцип работы.
Диодный универсальный функциональный преобразователь воспроизводит кусочно-линейную аппроксимацию заданной функции f(UВХ) т.е. вместо функции f(UВХ) он воспроизводит функцию F(UВХ) (см. рис. 2.5), которая не выходит за пределы трубки допусков, изображенной пунктирными линиями.
Функцию F(UВХ), состоящую из последовательно соединенных прямолинейных отрезков a-m, a-m+1,…, a0, a1, …,an-1, an (см. рис. 2.6), можно представить в виде суммы m+1+n функций F-m(UВХ), F-m+1(UВХ), …, F0(UВХ), F1(UВХ), …, Fn-1(UВХ), Fn(UВХ).
Функции Fi(UВХ) можно разбить на пять типов:
1)Функция F0(UВХ) .воспроизводящая функцию F(UВХ) на отрезке a0.
2) Функции, расположенные в первом квадранте координатной плоскости, например, функции F2(UВХ) и F3(UВХ)
3) Функции, расположенные во втором квадранте координатной плоскости, например, функция F-1(UВХ)
4) Функции, расположенные в третьем квадранте координатной плоскости, например, функции F-2(UВХ) F-3(UВХ).
5) Функции, расположенные в четвертом квадранте координатной плоскости, например, функция F1(UВХ)
Функцию F0(UВХ) можно представить в виде суммы двух функций
F0(UВХ)=F0(0)+K0UВХ
и воспроизвести с помощью суммирующего усилителя.
Функцию Fi(UВХ) любого из остальных четырех типов можно воспроизвести с помощью решающего усилителя с диодом во входной цепи.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.