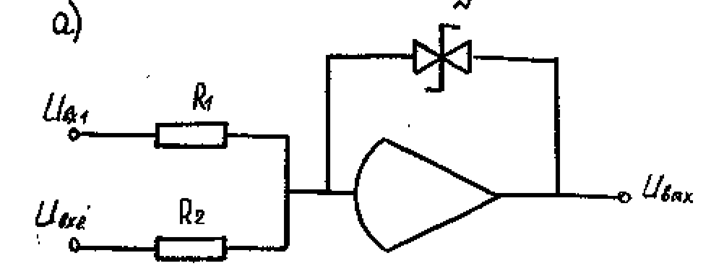
+a при (UВХ1+ UВХ2)<0
UВЫХ =
-a при (UВХ1+ UВХ2)>0
Частным случаем аналогового компаратора является .устройство, называемое функциональным реле. С его помощью выполняют логическую операцию условного перехода. Эта операция встречается в тех случаях, когда при моделировании САУ возникает необходимость воспроизвести скачкообразное изменение какого-либо параметра системы или сигнала. Такое изменение обычно требуется в момент выхода определенного сигнала за границы заданной области.
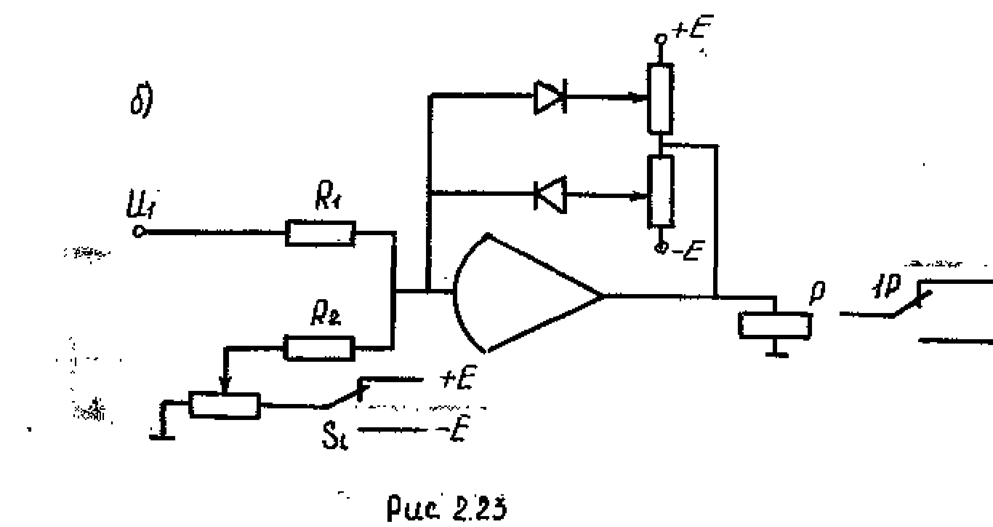
Схема моделирования логического устройства показана на рис. 2.236. ОУ нагружен обмоткой поляризованного реле Р, имеющего группу переключающих контактов. С помощью потенциометра R3 устанавливается уровень сигнала U1, при котором происходит переключение контактов реле. Знак напряжения U1 противоположен устанавливаемому переключателем S1.
Некоторые АВМ имеют в своем составе функциональные реле в виде отдельных блоков.
Лекция №19
1. Воспроизведение модульной характеристики
2. Воспроизведение люфта
3. Воспроизведение движения тела при наличии сил сухого трения
5. Диодный функциональный преобразователь, воспроизводящий модульную характеристику.
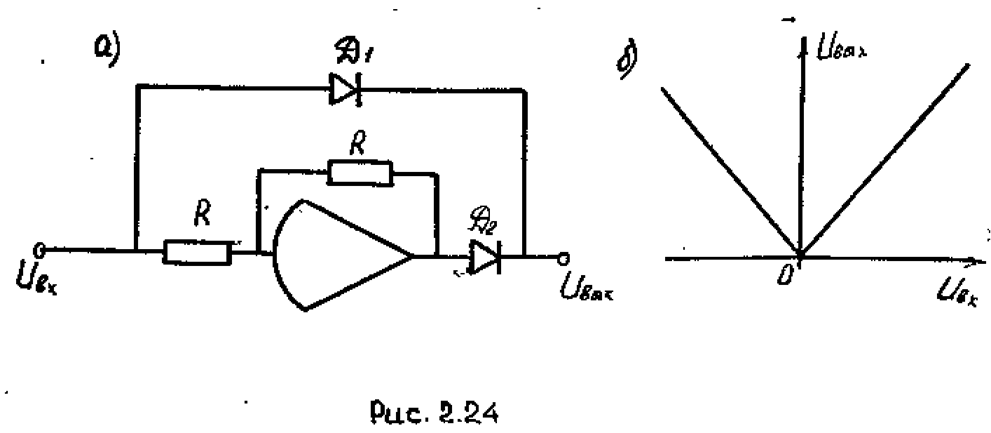
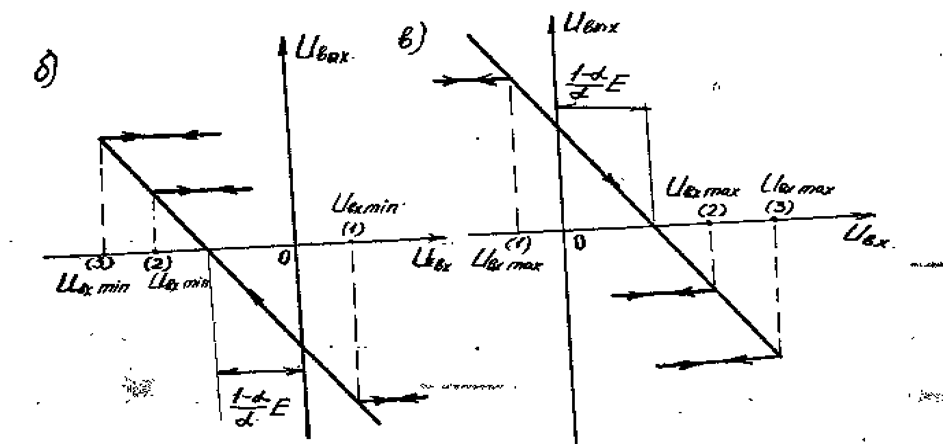
Схема преобразователя для воспроизведения модульной характеристики представлена на рис. 2.24а. В схеме положительный сигнал беспрепятственно проходит от входа к выходу черед диод D1. Отрицательный сигнал через диод D2 не пройдет, но после инвертирования на ОУ он становится положительным и поступает на выход через диод D2. График зависимости между выходным и входным напряжениями представлен на рис. 2.24б.
6. Диодный функциональный преобразователь, воспроизводящий люфт (зазор в передаче, гистерезис)
Люфт в несиловой передаче встречается в приборных САУ, в автоматических системах, имеющих редуктор с большим передаточным числом и т.д. (когда нагрузка не оказывает существенного влияния на поведение исполнительного двигателя системы)
Для моделирования такого вида люфта используется схема преобразователя, представленная на рис. 2.25а.
Схема может находиться в одном из трех состояний:
1) диод D1 открыт, а диод D2 закрыт;
2) диод D1 закрыт, и диод D2 закрыт;
3) диод D1 закрыт, а диод D2 открыт.
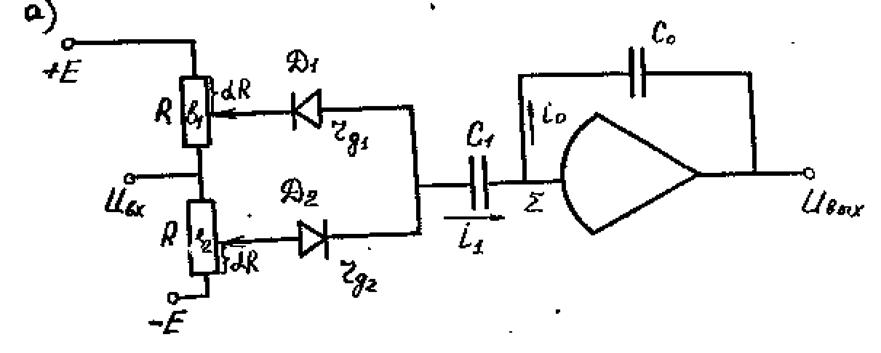
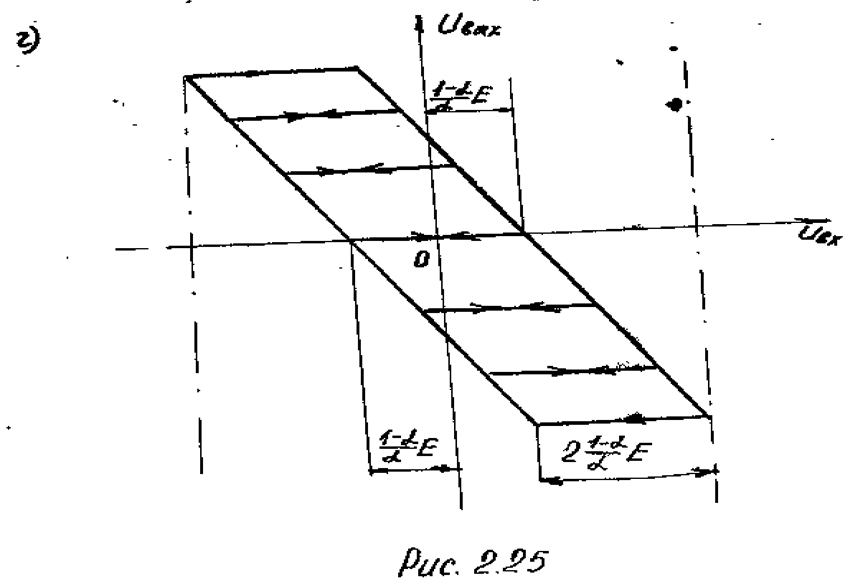
Пребывание обоих диодов в открытом состоянии для рассматриваемой схемы невозможно. Действительно, для схемы выполняется условие UВ1³UВ2 , а пребывание обоих диодов в открытом состоянии возможно лишь при выполнении противоречащего этому условию неравенства UВ1<UВ2
Рассмотрим работу схемы.
Токи i1 и i0 определяются выражениями
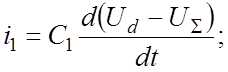
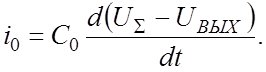
Согласно уравнению (1.2).
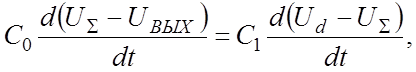
откуда, полагая US=0
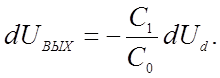
Интегрируя это уравнение в пределах: Ud от 0 до Ud, UВЫХ от UВЫХ0 до UВЫХ, имеем
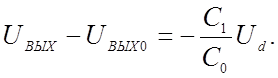
Если при Ud=0 разрядить конденсатор емкостью С0, то UВЫХ0=0 и
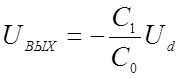 (a)
(a)
Если диоды закрыты, то согласно уравнению (1.17a)
UВ1=aUВХ+(1-a)E, (б)
UВ2=aUВХ-(1-a)E. (в)
Уравнение (б) или (в) будет несправедливо, если соответствующий диод будет открыт, т.е. через него будет протекать ток. Однако, величины резистора R и емкости C1 таковы, что ток, протекающий через открытый диод, значительно меньше тока, протекающего через резистор R, поэтому можно считать, что уравнение (б) или (в) остается справедливым и тогда, когда соответствующий диод открыт.
Рассмотрим первое и второе состояния схемы и условия её перехода из одного состояния в другое состояние. Предположим, что схема находится в первом состоянии, при котором rg1=0, rg2=¥, Ud=UВ1.
Если напряжение UВХ будет уменьшаться, то, как доказывает уравнение (б), напряжение Uв1 также будет уменьшаться. При этом диод D1 будет оставаться открытым и схема будет оставаться в первом состоянии. Напряжение Ud при этом будет равно напряжению UВ1, т.е.
Ud=UВ1=aUВХ+(1-a)E.
Подставляя это выражение Ud в уравнение (а), получаем
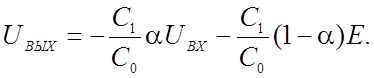 (2.40)
(2.40)
Таким
образом, при первом состоянии схемы напряжение
UВЫХизменяется по закону прямой линии,
пересекающей ось абсцисс (UВЫХ=0)
при 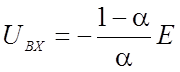 .
.
Если напряжение UВХ после достижения некоторого значения UВХmin начнет увеличиваться, то напряжение UВ1 также начнет увеличиваться. При этом диод D1 закроется и, пока диод D2 будет оставаться закрытым, схема будет находиться во втором состоянии. Напряжение Ud при этом будет сохранять значение UВ1min, т.е.
Ud=UВ1min=aUВХmin+(1-a)E.
Подставляя это выражение Ud в уравнение (а), получаем
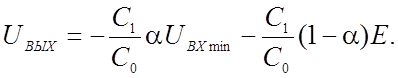 (2.41)
(2.41)
Таким образом, при втором состоянии схемы напряжение UВЫХ не изменяется; если напряжение UВХ снова начнет уменьшаться и станет меньше UВХmin, то диод D1 опять откроется и схема опять перейдет в первое состояние и т.д.
На рис. 2.25б изображен график уравнения (2.40), на котором стрелками указаны направления возможных переходов схемы из первого состояния во второе состояние и наоборот.
Рассмотрим второе и третье состояния схемы и условия ее перехода из одного состояния в другое состояние. Предположим, что схема находится во втором состоянии, при котором
Rg1=¥, rg2=¥, Ud=UВ1 min.
Если напряжение UВХ будет продолжать увеличиваться, то напряжение UВ2 также будет продолжать увеличиваться. Когда UВ2 станет больше UВ1 min, то диод D2 откроется, схема перейдет в третье состояние. Если UВХ будет продолжать увеличиваться, то UВ2 будет увеличиваться. При этом диод D2 будет оставаться открытым и схема будет оставаться в третьем состоянии. Напряжение Ud при этом будет равно напряжению UВ2, т.е.
Ud=UВ2=aUВХ-(1-a)E
Подставляя это выражение Ud в уравнение (а), получаем
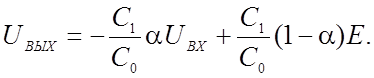 (2.42)
(2.42)
Таким
образом, при третьем состоянии схемы напряжение ![]() изменяется
по закону прямой линии, пересекающей ось абсцисс
изменяется
по закону прямой линии, пересекающей ось абсцисс![]() (
(![]() ) при
) при![]()
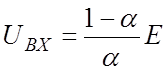 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.