Основы математического и физического моделирования систем управления, страница 27

1.  Учёт переходной характеристики звена. При ступенчатом входном воздействии выбор масштабов преобразования переменных должен производиться с учётом переходной характеристики звена . Очевидно, масштабы преобразования должны .удовлетворять соотношению

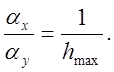
1) Апериодическое звено.

Передаточная функция

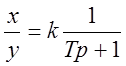
Переходная характеристика изображена на рис. 5.1а. Очевидно, что

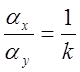
2) Дифференцирующее звено.

Передаточная функция

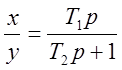
Переходная характеристика изображена на рис. 5.2а.

Очевидно, что

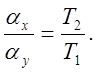
3) Интегро-дифференцирующее звено.

Передаточная функция

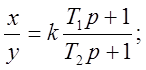
Переходная характеристика изображена на рис. 5.За.

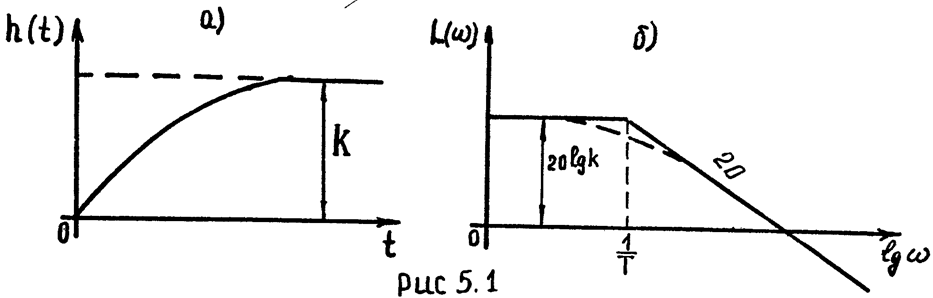
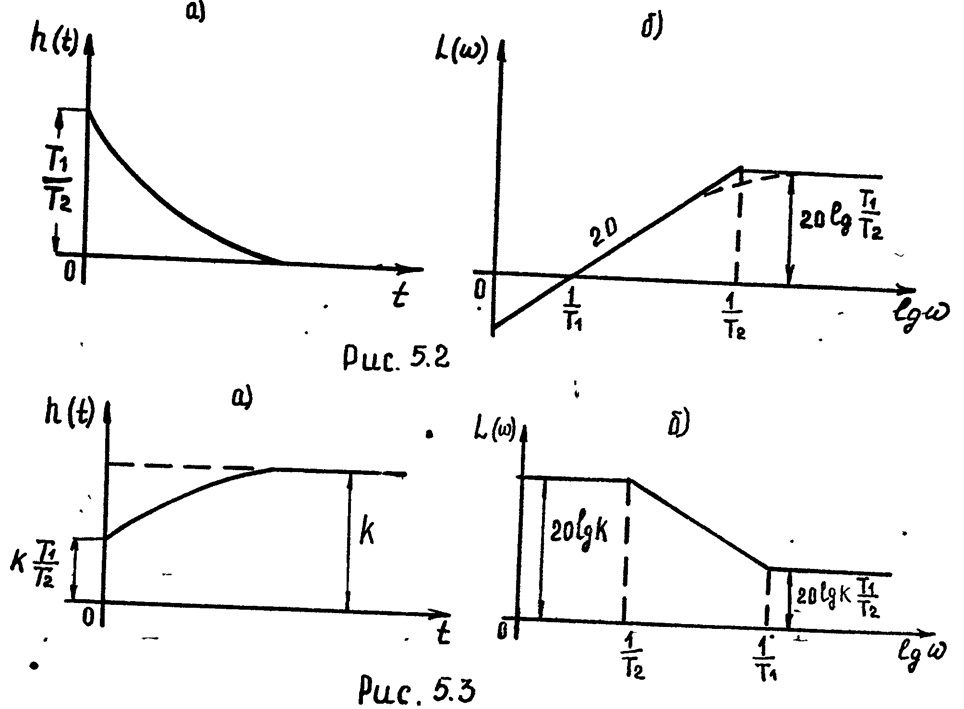
Очевидно:

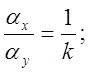
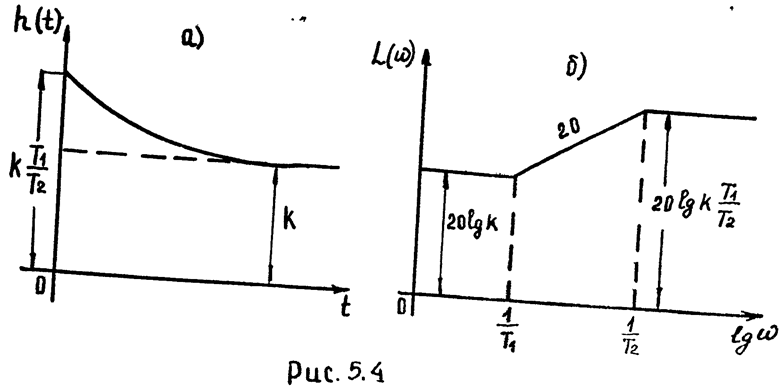
Переходная характеристика изображена на рис.      5.4а.

Очевидно:

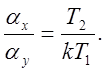
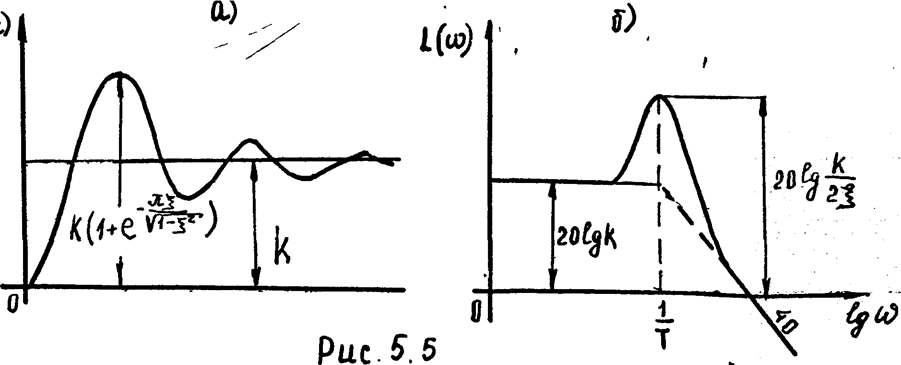
4) Колебательное звено,

Передаточная функция

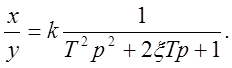
Переходная функция изображена на рис. 5.5а, Очевидно:

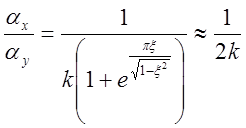
при предположении о максимально допустимом перерегулировании в 100%

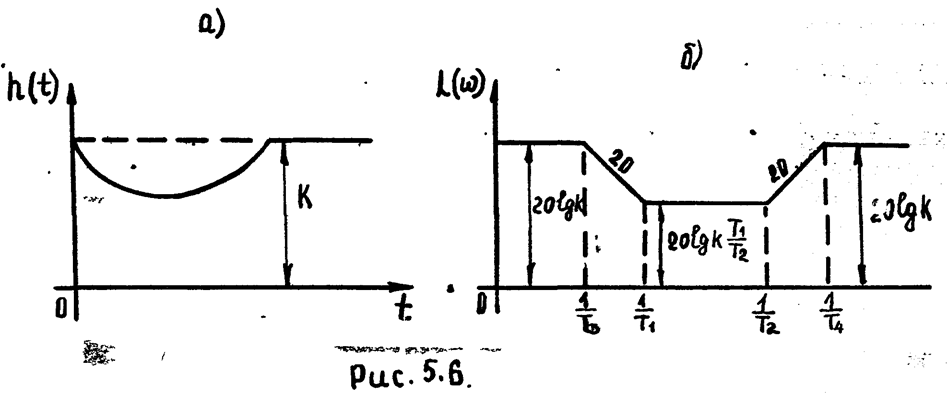
5) Звено, передаточная функция которого:

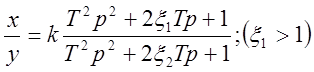                              (5.5)

а) 1<x₁>x₂

Переходная характеристика изображена на рис. 5.6а.

Очевидно:

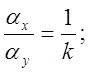
Переходная характеристика изображена на рис. 5.7а.

Величина 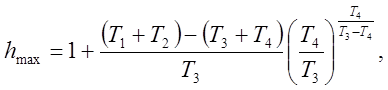 где

 

 

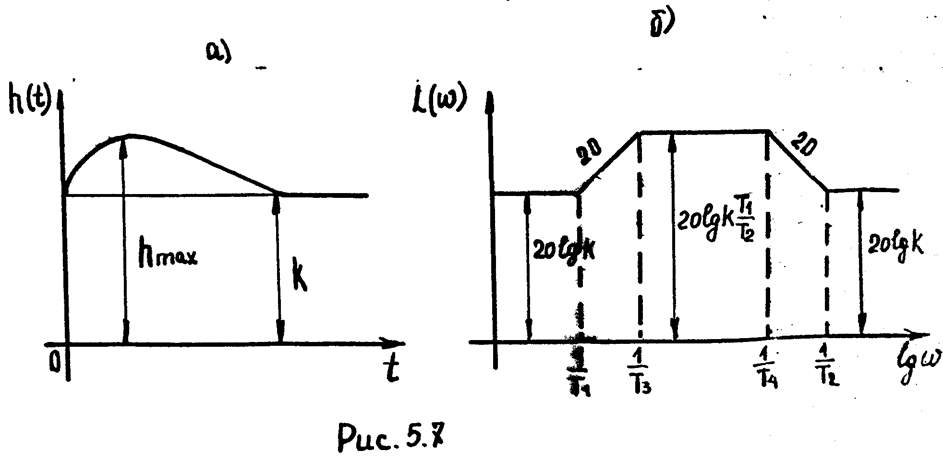
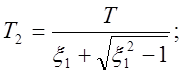
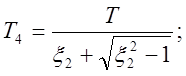
Очевидно,

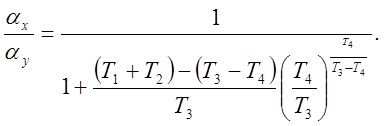
2.  Учёт амплитудной частотной характеристики звена. При гармоническом входном воздействии выбор масштабов преобразования переменных должен производиться с учётом амплитудной частотной характеристики звена (рис 5.16-5.76),

Амплитудная частотная характеристика звена с передаточной функцией

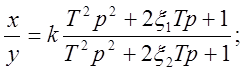
имеет экстремум

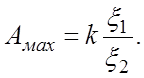
при

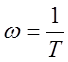
5.2. ПОЛУЧЕНИЕ МАШИННОЙ ПЕРЕДАТОЧНОЙ ФУНКЦИИ ЗВЕНА

 Для получения машинной передаточной функции звена необходимо заменить в заданной передаточной функции исходные переменные машинными переменными и исходный оператор машинным оператором, используя уравнения преобразования.

В качестве примера получим машинную передаточную функцию интегро-дифференцирующего звена, передаточная функция которого

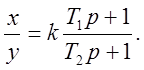
Заменяем в заданной передаточной функции исходные пе­ременные машинными переменными и исходный оператор машинным оператором, используя уравнения преобразования (4.2) и (4.1а):

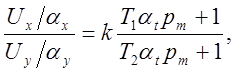
откуда:

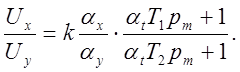
Лекция №30

План.

1. Схемы моделей динамических звеньев, построенные на элементарных решающих усилителях.

2. Зависимости для расчета коэффициентов передачи  решающих усилителей.

5.5. Составление схем модели звена и определение его параметров

Модель звена может быть построена двумя способами:

1) с помощью нескольких элементарных решающих усилителей;

2) с помощью одного решающего усилителя с "R-С" цепями во входной цепи и в цепи обратной связи.

В обоих случаях схема модели звена составляется в соответствии с его машинной передаточной функцией.

1. Составление схемы модели звена для ее построения с помощью элементарных решающих усилителей.

1) Схема модели апериодического звена.

Машинная передаточная функция (см. уравнение (5.1))

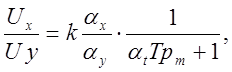                                           (5.6)

откуда:

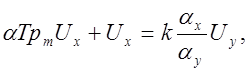
или:

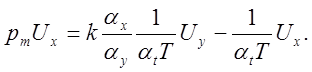
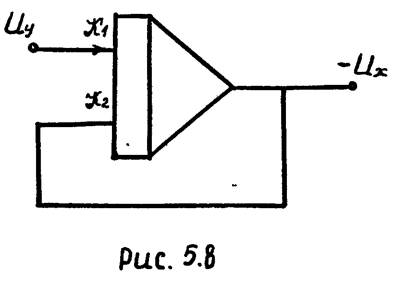
Схема модели апериодического звена, составленная в соответствии с уравнением (5.6а), изображена на рис. 5.8. Очевидно:

 

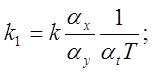
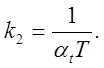
2) Схема модели дифференцирующего звена. Машинная передаточная функция (см. уравнение (5.2)):

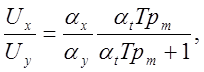                                   (5.7)

откуда:

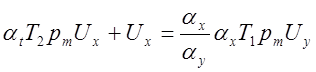
или:

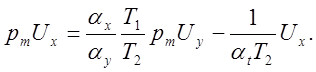                               (5.7а)

При моделировании по возможности избегают применения дифференцирующих усилителей вследствие их повышенной чувствительности к помехам, поэтому преобразуем уравнение (5.7а) следующим образом:

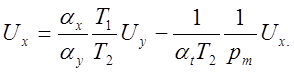                                (5.76)

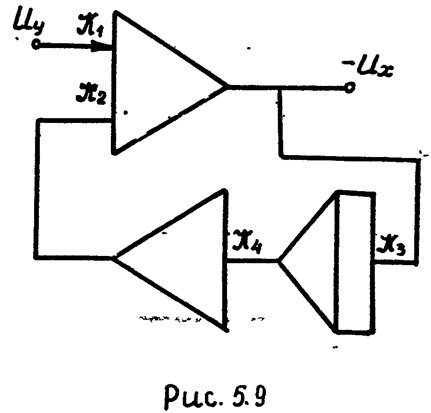
Схема модели дифференцирующего звена, составленная в соответствии с уравнением (5.76), изображена на рис. 5.9.

Очевидно:

 

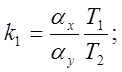
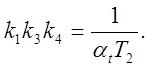
3)  Схема модели интегро-дифференцирующего звена.

          Машинная передаточная функция (см. уравнение (5.5)

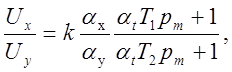
откуда:

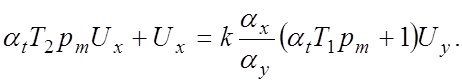
Умножим обе части подученного уравнения на Т₁ и прибавим затем к левой части :

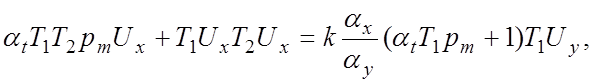
тогда

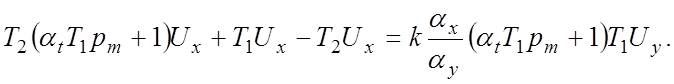
Следовательно:

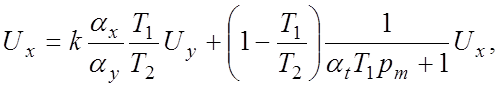
если T₁<T₂, или:

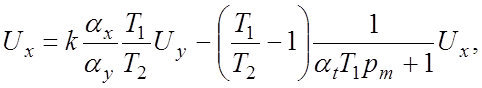
если T₁>T₂.

Множители, стоящие в уравнениях (5.8а) и (5.86) перед U_x, представляют собой машинные передаточные функции апериодического звена. Следовательно, выходную величину U_x необходимо подать на вход суммирующего усилителя через модель апериодического звена.

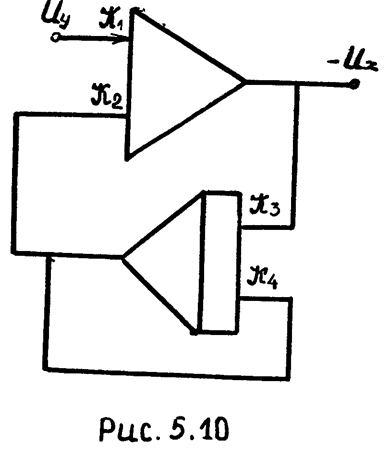
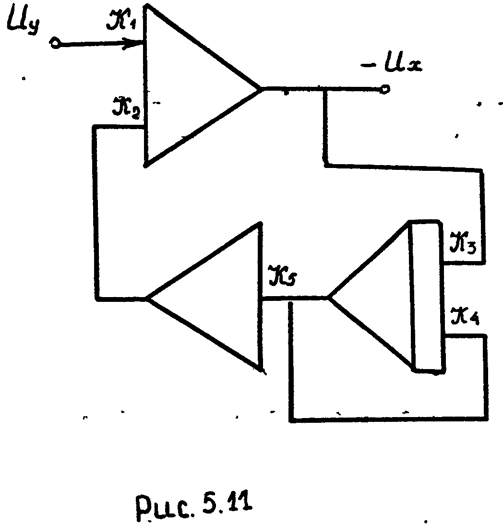
Схемы моделей интегро-дифференцирующего звена, составленные в соответствии с уравнениями (5.8а) и (5.8б), изображены на (5.10) и (5.11).

Очевидно:

 

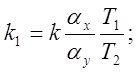
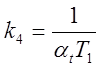
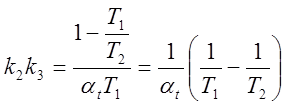, если T₁<T₂;

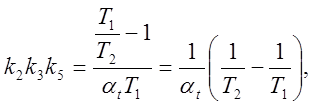если T₁>T₂.

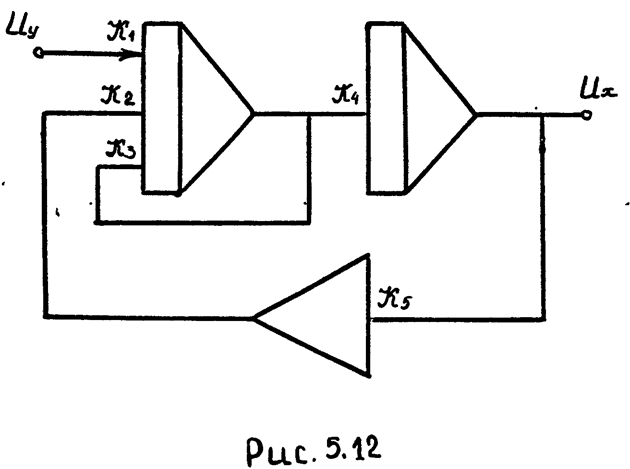
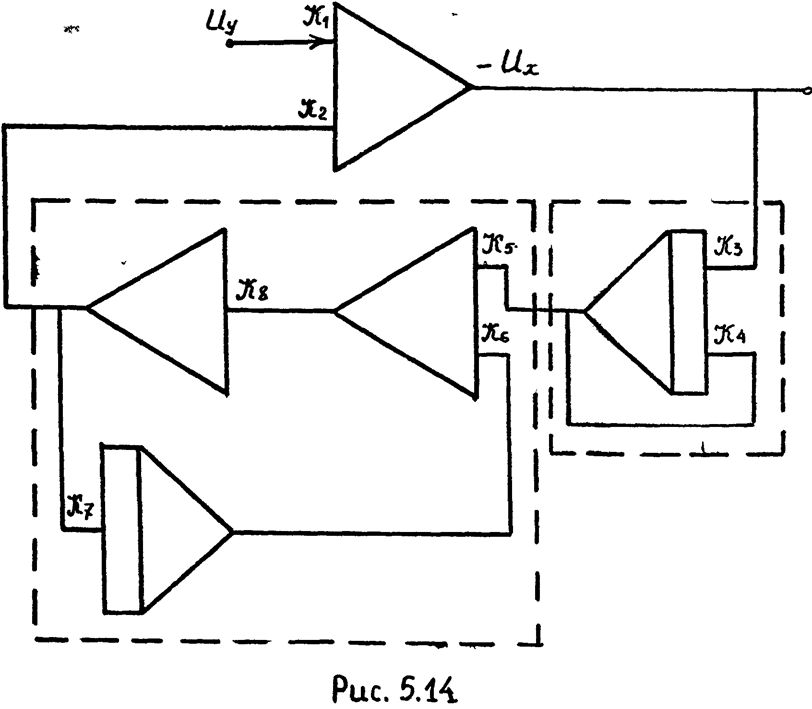
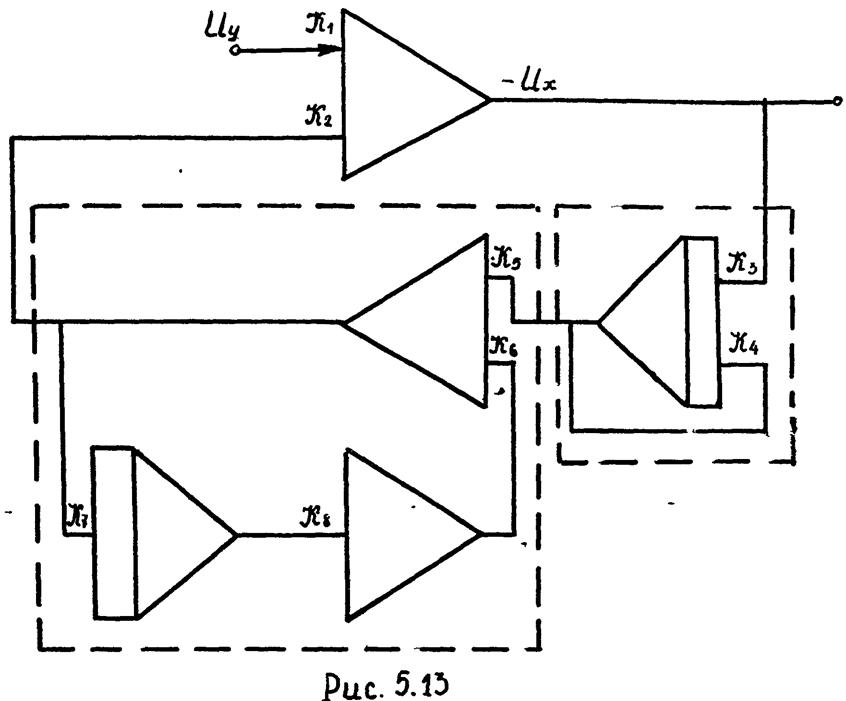
4) Схема модели колебательного звена (рис. 5.12). Машинная передаточная функция (см. уравнение 5.4)

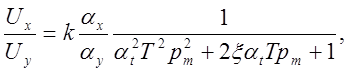                            (5.9)

откуда:

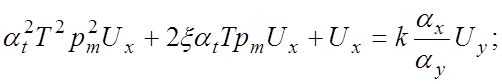
или:

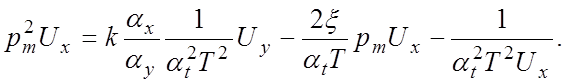                      (5.9а)

Очевидно:

  

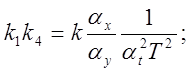
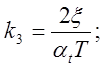
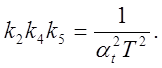
5) Схема модели звена, передаточная функция которого описывается уравнением (5.5).

Машинная передаточная функция:

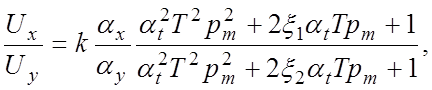                               5.10)

откуда

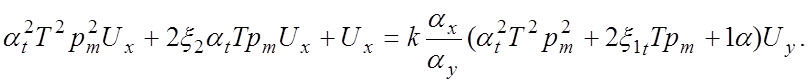
Прибавив к левой части полученного уравнения , получаем:

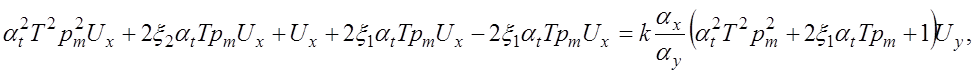
тогда:

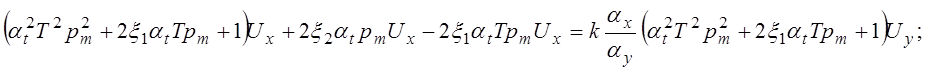
или:

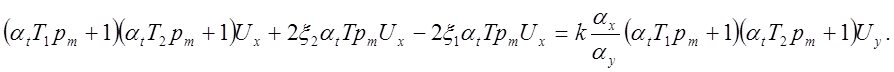
Величины Т₁ и Т₂ определяются соотношениями:

 

откуда:

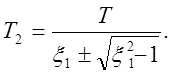
Следовательно:

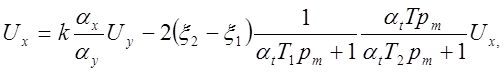 если ,

или

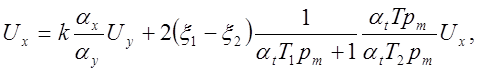 если .

Множители, стоящие в уравнениях (5.10а) и (5.106) перед U_х, представляют произведения машинных передаточных функций апериодического и дифференцирующего звеньев. Следовательно, выходную величину U_х необходимо подать на вход суммирующего усилителя через модели апериодического и дифференцирующего звеньев.

Схемы моделей рассматриваемого звена, составленные в соответствии с уравнениями (5.10а) и (5.106) , изображены на рис. 5.15 и 5.14 . Очевидно,

  

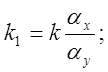
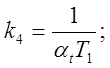
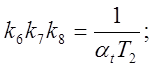
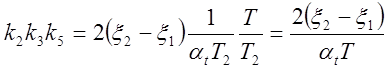, е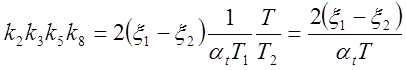сли ;

, если

Лекция №31

План

1. Схемы моделей динамических звеньев, построенные на решающих усилителях с PC - цепями в обратной связи и во входных цепях.

2. Зависимости для расчета параметров схем моделей звеньев.

3. Числовые примеры определения параметров модели звена.

2. Составление схемы модели звена для её построения с помощью решающего усилителя с "R-C" цепями во входной цепи и в цепи обратной связи.