











































Во второй и третьей главах получены уравнения на базе самых общих свойств деформируемой среды. Эти уравнения пригодны для любых тел независимо от свойств материала, из которого состоит тело, и процессов изменения деформаций с течением времени. Последние факторы учитываются уравнениями состояния деформируемой среды. Уравнения состояния часто называют определяющими уравнениями и конституционными уравнениями. Они определяют реакцию сплошной среды на внешние воздействия, которая существенным образом зависит от состояния среды. Уравнения состояния представляют собой математическую модель среды (материала деформируемого тела) и связывают между собой параметры ее состояния, отражая внутренние связи между ее элементарными частицами. В настоящей главе рассмотрены наиболее употребляемые математические модели материала, из которого состоят твердые деформируемые тела.
Во второй главе получены геометрические уравнения,
отражающие концепцию сплошности деформируемого тела, а в третьей главе –
уравнения движения, выражающие законы природы в механике сплошных сред. Эти
уравнения связывают компоненты вектора перемещений ![]() с
компонентами тензора деформаций
с
компонентами тензора деформаций ![]() и
напряжений
и
напряжений ![]()
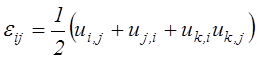 ,
, ![]() ;
(4.1)
;
(4.1)
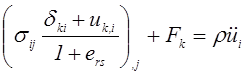 ,
, ![]() ,
(4.2)
,
(4.2)
см. (2.9) и (3.46). Есть еще уравнения сплошности (п. 2.11.1), но они
представляют собой лишь ограничения, накладываемые на компоненты тензора деформаций,
при которых обеспечивается сплошность деформируемого тела, и при подстановке
компонент вектора перемещений обращаются в тождества. Поэтому независимыми
оказываются только 6 уравнений геометрии перемещения сплошной среды (4.1) и 3
уравнения движения (4.2). В эти 9 уравнений входят 15 неизвестных функций: 3
функции перемещений ![]() , 6 компонент
тензора деформаций
, 6 компонент
тензора деформаций ![]() и 6 компонент
тензора напряжений
и 6 компонент
тензора напряжений ![]() . Отсюда следует,
что для определения 15 неизвестных функций необходимы еще 6 независимых уравнений.
. Отсюда следует,
что для определения 15 неизвестных функций необходимы еще 6 независимых уравнений.
Таким образом, из условия замкнутости системы уравнений механики деформируемого твердого тела уравнения (4.1), (4.2) должны быть дополнены еще шестью независимыми уравнениями. С физической точки зрения это должны быть уравнения, отражающие специфические свойства конкретного материала, из которого состоит деформируемое тело. Эти уравнения носят название уравнений состояния твердого деформируемого тела. Их называют также физическими, определяющими и конституционными уравнениями. Они определяют реакцию материала, из которого состоит деформируемое тело, на внешние воздействия. Уравнения состояния представляют собой математическую модель материала деформируемого тела, связывая между собой параметры состояния сплошной среды. Для твердого деформируемого тела в качестве основных параметров состояния принимаются компоненты тензоров напряжений и деформаций или скоростей деформаций. Их общее количество равно 12-ти. Но, поскольку для замыкания общих уравнений механики сплошных сред требуется всего 6 уравнений, то из 12-ти основных параметров состояния независимыми оказываются всего 6.
В последнее время все большее значение приобретают задачи изучения движения деформируемых тел при воздействии на них температуры, электромагнитных и иных физических полей. При решении таких задач приходится вводить дополнительные параметры состояния и дополнительные уравнения, описывающие соответствующие физические явления. Так, например, при воздействии на деформируемое тело температурного поля в качестве дополнительных параметров состояния вводятся температура и энтропия, причем любая из них может быть независимой величиной. Обычно за независимый параметр состояния в этом случае принимают температуру. Поскольку вводятся дополнительные параметры состояния, то должны быть и дополнительные уравнения, которые их связывают между собой. При учете температурного поля таковым является уравнение теплопроводности.
В основу теории построения уравнений состояния в
механике сплошных сред положен постулат макроскопической определимости [4]. Он
может быть сформулирован следующим образом: если для данной среды задан процесс деформации
![]() и поток немеханических
видов энергии
и поток немеханических
видов энергии ![]() , оказывающих
влияние на свойства среды, то возникающие в ней напряжения
, оказывающих
влияние на свойства среды, то возникающие в ней напряжения ![]() в любой момент времени
в любой момент времени ![]() однозначно определяется
природой вещества, из которого состоит среда, и начальными значениями
однозначно определяется
природой вещества, из которого состоит среда, и начальными значениями ![]() ,
, ![]() в каждой точке среды. При
этом под процессом деформации понимаются непрерывно дифференцируемые по времени
функции
в каждой точке среды. При
этом под процессом деформации понимаются непрерывно дифференцируемые по времени
функции ![]() в промежутке
в промежутке ![]() .
.
![]() ,
, ![]() .
(4.3)
.
(4.3)
Можно сделать и обратное заключение:
если задан процесс нагружения ![]() и поток немеханических
видов энергии
и поток немеханических
видов энергии ![]() , то тем самым
однозначно определяются деформации
, то тем самым
однозначно определяются деформации
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.