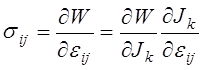Уравнения состояния твердого деформируемого тела. Общие принципы построения уравнений состояния. Постулат макроскопической определимости, страница 8

       .                                                 (4.37)

На основании (2.28) равенства (4.37) приводятся к виду

;

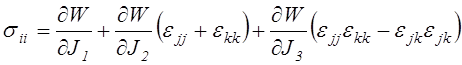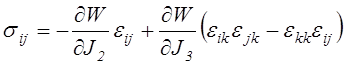   , ,  .              (4.38)

Формулы (4.38) в наиболее общем виде представляют зависимость между компонентами тензоров напряжений и деформаций. Для практического использования этих формул необходимо знать три функции , которые определяют механические свойства материала. Эти функции с помощью (4.38) могут быть легко выражены через главные компоненты тензоров напряжений и деформаций. Последние выражения могут использоваться для экспериментального определения функций .

Для изотропных материалов при малых деформациях и перемещениях часто принимают, что . Это допущение позволяет существенным образом упростить формулы (4.38).

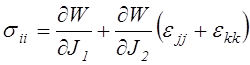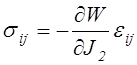,  ,   ,   .       (4.39)

Сложив между собой первые три соотношения (4.35), получим, имея в виду (2.43) и (3.31), зависимость между компонентами шаровых тензоров напряжения и деформации:

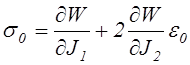.                                             (4.40)

Вычтя (4.40) из (4.39)получим зависимость между девиаторами тензоров напряжений и деформаций

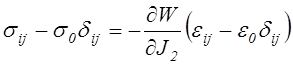.                                   (4.41)

Для того, чтобы установить значение величины  поступим следующим образом. Подставим выражения (4.39) в формулу (3.33), имея в виду (2.49). Тогда получим

.

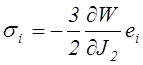Отсюда

.

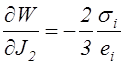В результате уравнения (4.41) принимают вид

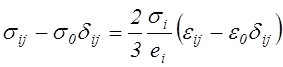                                     (4.42)

Для линейно упругого материала

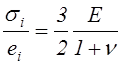,                                                  (4.43)

см. (4.33), и уравнения (4.42) приводятся к уравнениям (4.32). Разрешив уравнения (4.42) относительно компонент тензора деформаций, получим

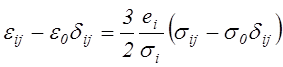.                                      (4.44)

Полагая, что объемная деформация является линейно-упругой и для нелинейного упругого материала подчиняется закону (4.31), преобразуем уравнения (4.44) следующим образом

.

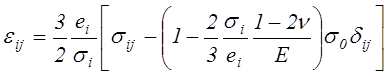Придадим последним уравнениям такой же вид, как у линейно упругого материала, см. (4.29),

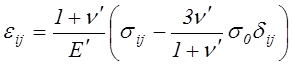,                                    (4.45)

где  и  носят название переменных параметров упругости и определяются путем приравнивания соответствующих коэффициентов у двух последних уравнений

,                                      (4.46)

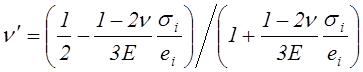.                                (4.47)

Переменные параметры упругости находятся путем обработки диаграммы, связывающей между собой интенсивности напряжений и деформаций при линейном напряженном состоянии, полагая, что связь между  и  не зависит от вида напряженного состояния. Подставив (4.43) в (4.46) и (4.47), находим, что для линейно-упругого материала  и .

С другими известными подходами к построению уравнений состояния нелинейной упругости можно ознакомиться в монографиях и статьях, посвященных нелинейной теории упругости, например в [25].

4.4. Уравнения состояния теории пластичности

Главным признаком пластического состояния материала является образование после снятия нагрузки остаточных деформаций. При последующем нагружении того же материала его деформации вначале происходят практически по линейному закону (если не учитывать образование петли упругого гистерезиса) вплоть до напряжений, которые были достигнуты при первом нагружении. Отсюда следует, что на закономерности пластического деформирования материала большое влияние оказывает история предшествующего нагружения и деформирования. Пластическое состояние материала описывается более сложными закономерностями, чем упругое состояние. Полное исследование уравнений состояния в случае пластического деформирования различных материалов производятся в курсе теории пластичности. Здесь ограничимся рассмотрением общих подходов к построению уравнений состояния изотропных материалов и приведем некоторые уравнения состояния этих материалов.

4.4.1. Условия начала пластичности для изотропного материала

В случае однородной деформации растяжения или сжатия пластичность наступает при достижении напряжениями предела текучести , а в случае чистого сдвига – при достижении предела текучести при чистом сдвиге , которые легко устанавливаются опытным путем. Значительно сложнее определить начало образования пластических деформаций при сложном напряженном сотстоянии. В самом общем случае начало образования пластических деформаций может быть представлено следующим условием пластичности: