Уравнения состояния твердого деформируемого тела. Общие принципы построения уравнений состояния. Постулат макроскопической определимости, страница 11

Размеры, форма и положение поверхности пластичности S зависят не только от конечного деформированного состояния, но и от всей истории деформирования. Ясно, что эта поверхность должна быть выпуклой, так как в противном случае возможны ситуации, когда разгрузка будет сопровождаться пластическими деформациями. При достижении поверхности пластичности приращения компонентов напряжений  приводят либо к упругой разгрузке, если вектор  направлен внутрь поверхности S, либо к нагружению, при котором происходит рост пластических деформаций, если вектор  направлен наружу поверхности S, либо, наконец, к нейтральному нагружению, если вектор лежит в касательной плоскости к поверхности пластичности. В последнем случае материал деформируется упруго.

4.4.3. Постулат Друкера. Принцип максимума работы

пластической деформации

Рассмотрим удельную работу, затрачиваемую на бесконечно малое приращение пластических деформаций :

, где  – компоненты тензора напряжений перед приращением пластических деформаций . Приращение пластических деформаций вызывает соответствующее приращение компонентов тензора напряжений , которые являются бесконечно малыми по сравнению с . Это позволяет без ущерба для точности величины  записать

.

Наряду с этим рассмотрим удельную работу какого-то допустимого в упругой области деформирования напряженного состояния  при том же приращении пластических деформаций

, где   компоненты напряженного состояния, которые могут рассматриваться, как результат разгрузки после достижения состояния . Последнее обстоятельство позволяет утверждать, что  или

                 .                                   (4.59)

Неравенство (4.59)  является математической записью постулата Друкера, согласно которому работа добавочных напряжений за цикл нагружения и разгрузки положительна.

Если принять , то из неравенства (4. 59) получим

                .                                                (4.60)

Неравенство (4.60) рассматривается как критерий устойчивости деформирования за пределом текучести. Неравенство (4.60) выполняется в случае нагружения материала.

Если  то величина  может быть сколь угодно больше . Поэтому из равенства (4.59) имеем

     .                                             (4.61)

Неравенство (4.61) является математической формулировкой принципа максимума работы пластической деформации, согласно которому при любом заданном приращении пластической деформации приращение работы пластической деформации   имеет максимальное значение лишь для действительного напряженного состояния.

4.4.4. Ассоциированный закон течения

Принцип максимума работы пластической деформации позволяет на базе условия пластичности (4. 56) установить зависимость между компонентами тензора напряжений и приращением пластических деформаций. Нетрудно видеть, что приращение работы пластической деформации  является функцией компонентов , поскольку таковыми являются и приращения пластической деформации . Поэтому на основании принципа максимума работы пластической деформации для определения действительного напряженного состояния необходимо найти максимальное значение приращения работы пластической деформации. При этом следует иметь в виду, что компоненты тензора напряжений не могут рассматриваться в качестве независимых переменных, так как они связаны между собой условием пластичности (4.56). Поэтому условие относительного максимума функции приращения пластической работы  может быть найдено способом множителей Лагранжа

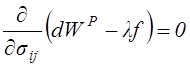, где l – множитель Лагранжа, a  – условие пластичности (4.56). Подставив сюда значение , найдем, что

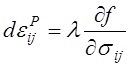                   .                                                (4.62)

Соотношение (4.62) является математическим выражением так называемого ассоциированного закона течения.

Предположив, что в результате пластических деформаций объем материала не изменяется, приходим к заключению, что компоненты приращения пластической деформации являются девиатором приращения пластической деформации. С девиатором связана интенсивность деформации. На основании формулы (2.76) интенсивность приращения пластической деформации равна