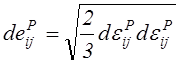 .
.
Подставив сюда (4.62), получим
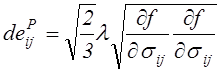 .
.
Отсюда находится величина множителя Лагранжа:
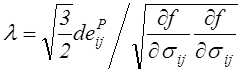 .
(4.63)
.
(4.63)
Предположение о
неизменности объема при пластических деформациях подтверждается результатами экспериментальных
измерений. Поэтому равенство (4.63) в теории пластичности можно считать фундаментальным.
Из этого равенства следует, что при пластическом деформировании,
т.е. при ![]() множитель Лагранжа l>0.
множитель Лагранжа l>0.
Непосредственно из формул (4.60) и (4.62) находим условия существования нагружения материала:
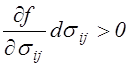 ,
,
![]() ,
, ![]() .
.
Условия существования разгрузки записываются следующим образом
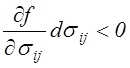 ,
,
![]() ,
, ![]() .
.
Это является
следствием того, что при разгрузке ![]() . При
напряженных состояниях, соответствующих точкам поверхности пластичности, имеем
. При
напряженных состояниях, соответствующих точкам поверхности пластичности, имеем
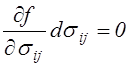 ,
,
![]() ,
, ![]() .
.
Это так называемый нейтральный тип нагружения. Для него законы упругости и пластичности должны совпадать, т.е. при нейтральном нагружении возникают только упругие деформации. Это является условием непрерывности при переходе от упругого деформирования к пластическому.
В зависимости от принятой поверхности пластичности можно построить различные теории. В случае, когда в процессе нагружения поверхность пластичности расширяется равномерно без учета эффекта Баушингера, упрочнение называется изотропным. Теория пластичности, построенная на базе такой поверхности пластичности, называется теорией течения с изотропным упрочнением или просто теорией течения.
Примем поверхность пластичности (4.56) в виде
![]() ,
(4.64)
,
(4.64)
где q – мера упрочнения, которую определим формулой (4.58) – параметр Удквиста. Тогда
![]() ,
(4.65)
,
(4.65)
т.е. интенсивность напряжений является функцией параметра Удквиста. Условие (4.65) является обобщением энергетического условия начала пластичности (4.65) на деформирование упрочняющегося материала в области пластических деформаций.
При построении любой теории пластичности приходится принимать гипотезы, которые позволяют получить количественную меру соответствия между сложным и линейным напряженными состояниями, т.е. чтобы по результатам испытаний на растяжение и сжатие стандартных образцов можно было бы найти зависимость между компонента ми сложного напряженного состояния и деформациями. В теории течения с использованием в качестве меры упрочнения параметра Удквиста используются следующие гипотезы: 1) образование пластических деформаций связано лишь с формоизменением элементов тела; 2) при пластических деформациях объем материала не изменяется (несжимаемость материала); 3) интенсивность напряжений является функцией Удквиста при любом напряженном состоянии; 4) интенсивности напряжений и деформаций найденные при линейном напряженном состоянии, справедливы и при сложном напряженном состоянии.
Преобразуем
условие (4.65)
применительно к линейному напряженному состоянию. При одноосном растяжении
имеем ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . На основании
гипотезы о несжимаемости материала при пластических деформациях
. На основании
гипотезы о несжимаемости материала при пластических деформациях ![]() . Откуда
. Откуда ![]() . На основании формул (3.33)
и (2.76) находим,
что при одноосном растяжении
. На основании формул (3.33)
и (2.76) находим,
что при одноосном растяжении ![]() ,
, ![]() и,
следовательно,
и,
следовательно,
![]() .
.
Таким образом, при линейном напряженном состоянии в случае растяжения формула (4. 65) приводится к виду
![]() .
(4.66)
.
(4.66)
Для определения множителя
Лагранжа l из формулы (4.63) необходимо найти производные ![]() .
С этой целью обратимся к формуле (3.33), на основании которой функция
.
С этой целью обратимся к формуле (3.33), на основании которой функция ![]() (4.64) запишется в виде
(4.64) запишется в виде
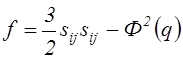 ,
,
![]() , где
, где
![]() . Тогда
. Тогда
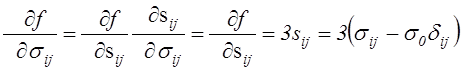 .
.
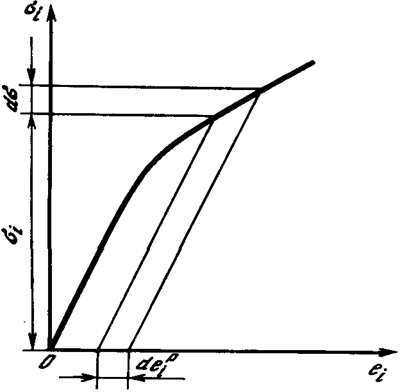
Подставив найденные значения производных в формулу (4.63), получим
 |
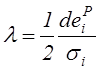 .
.
Рис. 21. Схема определения величины depi/si по диаграмме растяжения
Теперь на основании ассоциированного закона течения (4.62), можно связать приращения пластических деформаций с компонентами тензора напряжений
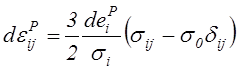 .
(4.67)
.
(4.67)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.