Уравнения состояния твердого деформируемого тела. Общие принципы построения уравнений состояния. Постулат макроскопической определимости, страница 6

Рис.17. Положительные направления напряжений s_ij при различных направлениях оси OX₃

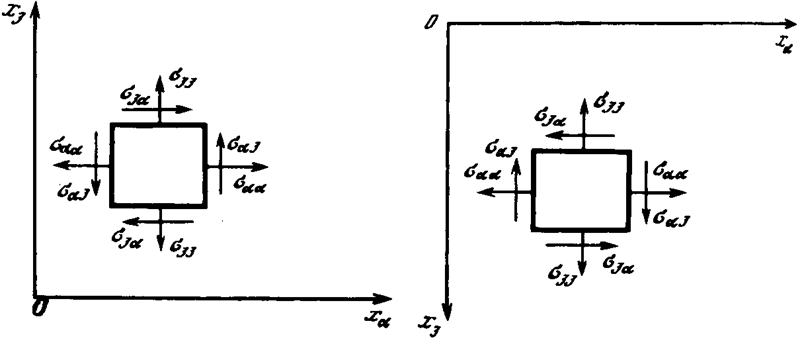
Для ортотропного материала, у которого имеется три плоскости упругой симметрии, возможно сокращение коэффициентов упругой податливости до 9. Но для этого необходимо, чтобы плоскости упругой симметрии были бы совмещены с координатными плоскостями. Тогда из условия неизменности потенциала деформаций при изменении направления всех координатных осей устанавливается равенство нулю коэффициентов  при любых компонентах  (i¹j) в первой степени. Для ортотропного материала широкое распространение получили, так называемые, технические постоянные. Уравнения закона Гука, выраженные через технические постоянные, в случае совмещения координатных плоскостей с плоскостями упругой симметрии записываются в виде

;

;  ;

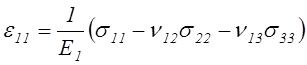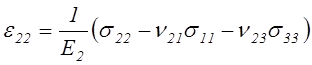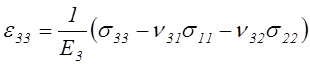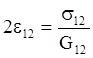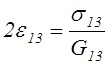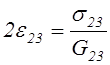  ;        ;         ;                       (4.26)

где , ,  – соответственно модули нормальной упругости, модули сдвига и коэффициенты Пуассона. При этом между модулями нормальной упругости и коэффициентами Пуассона существуют следующие зависимости:

;      ;        .

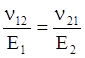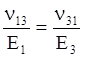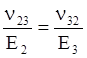При использовании анизотропных материалов, имеющих плоскости упругой симметрии, существенные упрощения в форме записи уравнений закона Гука, получаются лишь в тех случаях, когда с плоскостями упругой симметрии совмещаются координатные плоскости. В противном случае приходится применять уравнения закона Гука для самого общего случая анизотропии.

4.3.3. Уравнения закона Гука для изотропного материала

Изотропный материал характеризуется тем, что его упругие свойства во всех направлениях одинаковы. У изотропного материала любая ось является осью упругой симметрии. Поэтому упругий потенциал и потенциал деформаций изотропного материала не должны изменяться при изменении осей координат и их поворотах. Вследствие этого он должен выражаться через инварианты тензора деформаций. Единственная квадратичная форма, составленная из этих инвариантов, зависит от двух констант и выражается следующим образом:

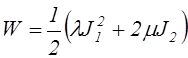            ,                                               (4.27)

где l и m носят название упругих постоянных Ламе, а , и  –инварианты тензора деформаций (2.28).

Упругая постоянная Ламе m численно равна модулю сдвига: .

Имея в виду, что при малых деформациях , см. (2.28) и (2.40), получим после подстановки (4.27) в (4.17) и представления  через компоненты тензора деформаций (2.28) следующие уравнения закона Гука

         ,                                                (4.28)

где  – символ Кронекера.

Уравнения закона Гука, разрешенные относительно компонентов тензора деформаций, легко представляются через технические постоянные: коэффициент Пуассона nи модуль нормальной упругости :

,      .

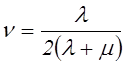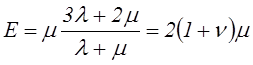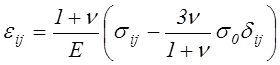           ,                                        (4.29)

где  – компоненты шарового тензора напряжений, см. (3.31).

Просуммировав диагональные компоненты тензора напряжения (4.28) , получим

.

Положим

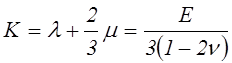            ,                                        (4.30)

тогда

            ,                                                      (4.31)

где –называется объемным модулем упругости.

Закон Гука записывают также относительно девиатора тензоров напряжения и деформации и относительно интенсивностей напряжения и деформации. В первом случае достаточно из (4.28) вычесть ,  имея ввиду (4.30), (4.31) и равенство , см. (2.43),

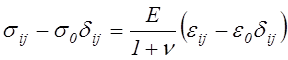                                                   (4.32)

Во втором случае следует (4.29) подставить в формулу (2.49). Тогда, используя формулу (3.33), получим

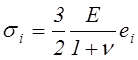            .                                                   (4.33)

Для положительно определенной квадратичной формы упругого потенциала необходимо и достаточно условие , . Из физических соображений следует также положительность модулей Е и К. Отсюда находится такое ограничение возможных значений коэффициента Пуассона: . Значение соответствует несжимаемому материалу. Опыт показывает, что для всех известных изотропных материалов коэффициенты Пуассона больше нуля. Следовательно, численные значения коэффициентов Пуассона ограничены промежутком (0, 0,5], т.е. .