Уравнения состояния твердого деформируемого тела. Общие принципы построения уравнений состояния. Постулат макроскопической определимости, страница 9

,                                                       (4.48)

куда входят механические характеристики, определяющие возникновение пластических деформаций при простейших видах напряженного состояния.

Очевидно, что возникновение пластических деформаций не зависит от принятой системы координат, поэтому условие начала пластичности может быть записано в виде функции инвариантов напряженного состояния (3.8) или (3.10). Как показывают опыты при всестороннем равномерном сжатии пластические деформации не возникают. Образование их связано исключительно с искажением формы объемного элемента. Поэтому условие начала пластичности может быть записано в виде функции инвариантов девиатора тензора напряжений (3.32)

.                                      (4.49)

В системе координат ,, уравнение (4.49) описывает цилиндр, образующие которого перпендикулярны к плоскости . Эта плоскость называется девиаторной, так как любой вектор, лежащий в ней, характеризует девиатор какого-то напряженного состояния. В силу равенства нулю первого инварианта девиатора напряжений, который по форме совпадает с уравнением девиаторной плоскости, при исследовании начала образования пластических деформаций достаточно рассмотреть след пересечения упомянутого цилиндра с девиаторной плоскостью. Этот след представляет собой замкнутую кривую, которая служит границей между упругой (внутренней) и пластической (внешней) областями. След пересечения цилиндра с девиаторной плоскостью показан на Рис. 18а, где через 1¢, 2¢, 3¢ обозначены проекции осей , ,   на девиаторную плоскость. Кривая, описывающая пересечения цилиндра с девиаторной плоскостью, должна обладать следующими свойствами: 1) не проходить через начало координат, так как пластические деформации возникают лишь при значительных напряжениях; 2) луч, проведенный из начала координат, должен пересекать кривую только один раз, так как в противном случае нет однозначности в определении начала пластичности; 3) кривая должна быть симметричной относительно осей 1¢, 2¢, 3¢, так как они равноправны вследствие изотропности материала; 4) при предположении одинаковых механических свойств материала в случаях растяжения и сжатия и пренебрежении эффектом Баушингера кривая должна быть симметричной относительно лучей, проходящих из начала координат и являющихся перпендикулярными к осям 1¢, 2¢, 3¢; 5) кривая должна быть выпуклой, так как в противном случае могли бы иметь место ситуации, при которых после возникновения пластичности дальнейший рост напряжений мог бы вызвать упругие деформации.

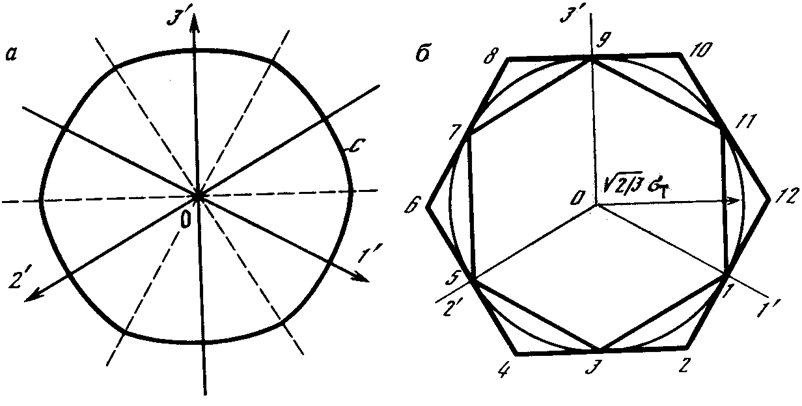
Рис.18. Следы пересечения поверхностей начала пластичности с девиаторной плоскостью

На основании изложенного заключаем, что эта кривая, которую будем называть кривой текучести, состоит из 12 одинаковых дуг, как это изображено на рис. 18а. Поэтому она должна быть заключена между правильными шестиугольниками 1-3-5-7-9-11 и 2-4-6-8-10-12, изображенными на рис. 18б так, что они проходят через точки на осях 1¢, 2¢ и 3¢ с координатами , где  предел текучести материала при растяжении или сжатии. Здесь множитель 2/3 равен косинусам углов между осями , и 1¢,  и 2¢,  и 3¢. По этой причине точки на осях 1¢, 2¢, 3¢ (точки 1, 5 и 9) соответствуют точкам на осях , , , координаты которых равны .

Уравнения граней указанных на рис. 18б шестиугольников, внутреннего и внешнего, имеют соответственно вид

,     ,                           (4.50)

и

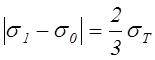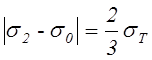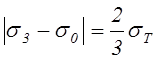      ,     ,     .               (4.51)

Уравнение окружности, описанной вокруг внутреннего и вписанной во внешний шестиугольник, имеет вид

  .                       (4.52)

На основании уравнений (4.50) условие начала пластичности оказывается следующим

                                                                         (4.53)

так как .