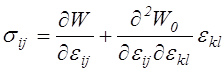Уравнения состояния твердого деформируемого тела. Общие принципы построения уравнений состояния. Постулат макроскопической определимости, страница 5

, где  – упругий потенциал в окрестности естественного состояния деформируемого тела.

Так как по определению естественного состояния , то на основании (4.17) первый член полученного равенства обращается в нуль, а само равенство приводится к виду

,                                                   (4.20) где  – модули упругости,

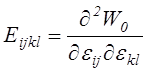         .                                                    (4.21)

Формула (4.20) выражает собой закон Гука. Входящие в него модули упругости, строго говоря, зависят от процесса деформирования, что предопределено соответствующей зависимостью упругого потенциала, см. п. 4.2. Модули упругости, определенные при изотермическом и адиабатическом процессах деформирования различны. Но для твердых тел это различие не существенно. Кроме того, они имеют общие свойства преобразования. Поэтому различия между ними делать не будем.

На основании формулы (4.21) заключаем, что модули упругости образуют тензор четвертого ранга. В виду симметрии компонентов тензоров напряжений и деформаций величины модулей упругости не изменяются при перестановке индексов i-j  и k-l. В результате из 81 компоненты тензора четвертого ранга в трехмерном пространстве различными окажутся лишь 21 компонента.

Формула (4.20) позволяет выразить упругий потенциал в явном виде только при одном условии, если упругий потенциал имеет квадратичную форму

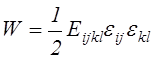.                                                  (4.22)

Ввиду того, что упругий потенциал представляет собой плотность работы внутренних сил, приходящей на единицу объема деформируемого тела, он всегда положителен. Поэтому квадратичные формы упругого потенциала положительно определенные.

Разрешим линейные уравнения (4.20) относительно компонентов тензора деформаций. Получим иную форму записи закона Гука:

,                                                      (4.23)

где – коэффициенты упругой податливости, которые образуют тензор четвертого ранга. В силу симметрии компонентов тензоров напряжений и деформаций из 81 компоненты тензора четвертого ранга различными будут лишь 21 компонента.

На основании (4.23) потенциал деформаций Ф принимает положительно определенную квадратичную форму

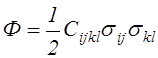             .                                                   (4.24)

Подставляя в (4.24) уравнения закона Гука в форме (4.23), а в (4.22) уравнения закона Гука в форме (4.20), находим, что для линейно упругого тела упругий потенциал и потенциал деформаций равны друг другу:

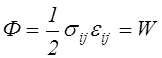.                                                   (4.25)

4.3.2. Уравнения закона Гука при наличии плоскостей упругой

симметрии в строении материала среды

Записи уравнений закона Гука в формах (4.20) и (4.23) относятся к самому общему случаю упругих свойств анизотропного материала. Однако часто анизотропные материалы имеют какую-то симметрию строения. Используя свойства симметрии, можно выбрать такую специальную систему координат, для которой некоторые модули упругости обращаются в нуль или становятся тождественно равными между собой. В результате общее количество коэффициентов, характеризующих упругие свойства материала, станет меньше чем 21. При этом за условие упругой симметрии принимается неизменность величины упругого потенциала Wили потенциала деформаций Ф  и их вида при изменении направления координатной оси на противоположное относительно оси или плоскости симметрии.

Допустим, что одна из координатных плоскостей, например плоскость x₁, x₂, является плоскостью симметрии упругих свойств. Это означает, что при изменении направления оси x₃ упругий потенциал W (4.20) и потенциал деформаций Ф (4.25) остаются неизменными. Но изменение направления оси x₃ на противоположное изменяет знак у компонентов  и , где a= 1,2. Это положение иллюстрируется Рис. I7, на котором показаны в плоскости x_ax₃ положительные значения компонентов  при двух различных направлениях оси x₃. Неизменность величины потенциала деформаций (4.25) при изменении знака у компонентов  возможна только в том случае, когда равны нулю коэффициенты  при компонентах  в первой степени. Приравняв соответствующие коэффициенты нулю, получим общее количество коэффициентов упругой податливости отличное от нуля равным 13.