Уравнения состояния твердого деформируемого тела. Общие принципы построения уравнений состояния. Постулат макроскопической определимости, страница 13

Из формулы (4.67) следует, что компоненты приращения пластической деформации пропорциональны компонентам девиатора напряжений. Входящая в формулу величина  находится по диаграмме растяжения образца при линейном напряженном состоянии в соответствии со схемой, приведенной на рис.21. Приращения компонентов упругой деформации на основании закона Гука в форме (4.29) принимают вид

.

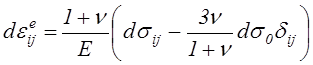Добавляя их к компонентам приращения пластической деформации (4.67), получим компоненты приращения полных деформаций

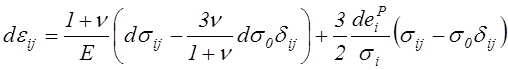                                  (4.68)

Эти соотношения являются основными уравнениями теории течения. Для случая плоской деформации они были предложены Прандтлем в 1924 г., а для общего случая Рейссом в 1930 г. Поэтому их иногда называют уравнениями Прандтля-Рейсса.

4.4.6. Теория малых упруго-пластических деформаций

В случае простого нагружения уравнения теории течения могут быть существенным образом упрощены. Здесь под простым понимается такое нагружение, при котором компоненты тензора напряжений возрастают пропорционально некоторому параметру t :

,

где  – значения компонентов тензора напряжений, например, в конце нагружения. В этом случае параметр t  изменяется в таких пределах:. В качестве параметра t может служить время нагружения.

Для простого нагружения зависимость (4.67) запишется в виде

,

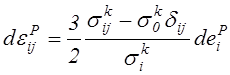где

.

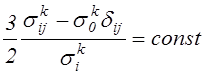Интегрируя эту зависимость от нулевых до конечных значений пластических деформаций, получим

.

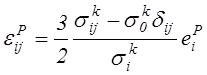После умножения знаменателя и числителя правой части на параметр t  имеем

.

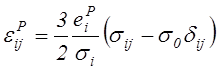Упругие составляющие компонентов деформации найдем  в соответствии с законом Гука в форме (4.29)

,

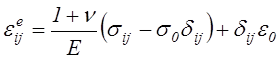так как .

Тогда

.

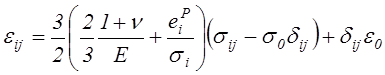На основании формулы (4.33) имеем

.

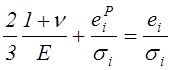Это позволяет предыдущую зависимость переписать в виде

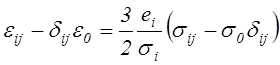,                                     (4.69)

где  и  – интенсивности деформаций и напряжений при одноосном растяжении, которые соответственно равны , . Так как при одноосном растяжении , то

.

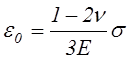Тогда

.

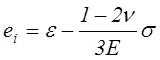С помощью этой формулы можно по диаграмме растяжения подсчитать величины  и , входящие в уравнение (4.69). Если принять условие несжимаемости, что равносильно допущению n=0,5, то .

Уравнения (4.69) являются основными уравнениями простейшего варианта деформационных теорий – теорий малых упруго-пластических деформаций. Впервые основные уравнения этой теории при отсутствии упрочнения были получены Генки. Упрочнение было рассмотрено Шмидтом. Уравнения в форме (4.69) были установлены А. А. Ильюшиным, который произвел детальный анализ и существенным образом развил эту теорию пластичности.

Уравнения (4.69), разрешенные относительно компонентов тензора деформаций, полностью совпадают с уравнениями (4.44), полученными применительно к нелинейно упругому материалу. Поэтому они могут быть преобразованы к виду (4.45), полностью совпадающему с уравнениями закона Гука. Переменные параметры упругости при этом определяются по формулам (4.46) и (4.47). Для несжимаемого материала, у которого n=0,5, формулы (4.46) и (4.47) позволяют получить следующие значения переменных параметров упругости:

,      .

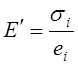Экспериментальные исследования показывают, что теория малых упруго-пластических деформаций дает удовлетворительные результаты не только при простом нагружении, но и при путях нагружения, близких к простому. Она справедлива в тех случаях, когда внешние силы, действующие на тело, растут от начала их приложения пропорционально общему параметру, например, времени. При более сложных путях нагружения используется теория течения.

4.4.7. Разгрузка. Остаточные напряжения и деформации

При построении теории пластичности считается, что интенсивность деформаций может быть представлена в виде суммы интенсивностей упругих и пластических деформаций. Поэтому диаграмма деформирования материала имеет такой же вид, как и диаграмма растяжения. В частности разгрузка будет происходить по прямой, параллельной первоначальному участку нагружения, см. рис. 22 .

Рис.22. Диаграмма деформирования при нагружении и разгрузке

Таким образом, разгрузка подчиняется упругому закону