- значительные по величине деформации ползучести при комнатной температуре.
Эти особенности требуют для расчета конструкций из неметаллических материалов иной нежели в предыдущем параграфе теории.
Основная
идея используемая при выводе наследственных соотношений ползучести или, как ее
еще называют, вязкоупругости состоит в том, что деформации ![]() зависят не
только от напряжений, которые действуют в тот же период времени t, но и от
всей совокупности напряжений
зависят не
только от напряжений, которые действуют в тот же период времени t, но и от
всей совокупности напряжений ![]() ,
, ![]() , действующих от
начала нагружения вплоть до времени t. Эта идея в случае одноосного
растяжения математически записывается следующим образом:
, действующих от
начала нагружения вплоть до времени t. Эта идея в случае одноосного
растяжения математически записывается следующим образом:
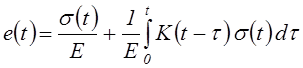 ,
(4.82)
,
(4.82)
где E – модуль
нормальной упругости; ![]() – разностное
ядро ползучести, которое характеризует "память" материала о предыдущих
воздействиях и отражает структурную устойчивость, т.е. неизменность свойств
материала во времени.
– разностное
ядро ползучести, которое характеризует "память" материала о предыдущих
воздействиях и отражает структурную устойчивость, т.е. неизменность свойств
материала во времени.
Интегральное соотношение (4.82) было впервые получено Больцманом и называется уравнением Больцмана.
Кривые ползучести многих конструкционных материалов и, в первую очередь полимеров и армированных пластиков, хорошо согласуются с уравнениями Больцмана (4.82) при использовании степенного ядра Абеля
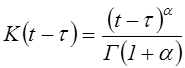 ,
, ![]() , где
, где ![]() –
гамма-функция:
–
гамма-функция:
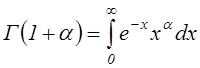 ;
;
n – показатель степенной зависимости, которая аппроксимирует кривые ползучести
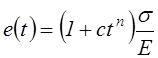 ,
, ![]() .
.
Заметим, что практическое определение гамма-функции не представляет никаких затруднений, так как в настоящее время для нее составлены подробные таблицы, которые приводятся в справочной литературе по математике.
Ядро
Абеля принадлежит к классу так называемых слабосингулярных ядер, у которых при
![]() скорость ползучести
скорость ползучести ![]() при конечном
значении деформации.
при конечном
значении деформации.
Теоретическое
построение кривой релаксации ![]() при
при ![]() на основе уравнения
Больцмана (4.82) связано с решением интегрального уравнения Вольтера II рода.
Решение имеет вид
на основе уравнения
Больцмана (4.82) связано с решением интегрального уравнения Вольтера II рода.
Решение имеет вид
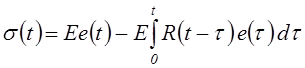 ,
(4.83)
,
(4.83)
где ![]() – ядро
релаксации, которое представляет собой, так называемую, резольвенту ядра
ползучести. Резольвента ядра Абеля найдена Ю. Н. Работновым и названа им
дробно-экспоненциальной функцией
– ядро
релаксации, которое представляет собой, так называемую, резольвенту ядра
ползучести. Резольвента ядра Абеля найдена Ю. Н. Работновым и названа им
дробно-экспоненциальной функцией
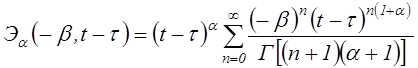 .
.
Если кривая ползучести описывается с помощью дробно-экспоненциальной функции в форме
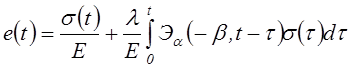 , то кривая релаксации
также выражается с помощью дробно-экспоненциальной функции, но с измененным
параметром ядра
, то кривая релаксации
также выражается с помощью дробно-экспоненциальной функции, но с измененным
параметром ядра
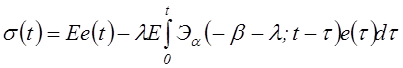 .
.
Дробно-экспоненциальная функция Работнова широко применяется для описания ползучести и релаксации полимеров в широком температурно-временном диапазоне, охватывающем области стеклообразного и высокоэластичного состояний, а также для описания ограниченной ползучести стекло- и угле-пластиков в направлении армирования. Для функции Работнова и интеграла от нее составлены таблицы.
Уравнение Больцмана
(4.82) с разностным ядром ![]() не может описать ползучесть материалов, у которых
со времнем происходит изменение свойств, не связанное с нагружением. Так,
например, свойства бетона, который твердеет в течение длительного времени,
изменяются с течением времени весьма существенно и это приходится учитывать при
расчете конструкций, изготовляемых из бетона. Изменение свойств материала с
течением времени носит название старения. В работах Г.Н. Маслова и Н.Х.
Арутуняна разработана наследственная теория старения, которая учитывает
старение таких материалов, как бетон.
не может описать ползучесть материалов, у которых
со времнем происходит изменение свойств, не связанное с нагружением. Так,
например, свойства бетона, который твердеет в течение длительного времени,
изменяются с течением времени весьма существенно и это приходится учитывать при
расчете конструкций, изготовляемых из бетона. Изменение свойств материала с
течением времени носит название старения. В работах Г.Н. Маслова и Н.Х.
Арутуняна разработана наследственная теория старения, которая учитывает
старение таких материалов, как бетон.
В наследственной теории старения при одноосном растяжении и сжатии принимается следующая закономерность
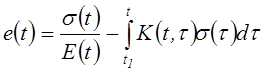 , (4.84)
, (4.84)
где неразностное ядро ![]() выражается через
модуль мгновенной упругости
выражается через
модуль мгновенной упругости ![]() , изменяющийся
во времени, и меру ползучести
, изменяющийся
во времени, и меру ползучести ![]()
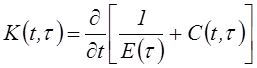 ;
;
t1 – временная константа материала.
Для бетона обычно используются экспоненциальные ядра. При этом в случае небольшой ползучести принимают
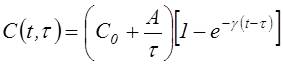 , где С0 , A,
, где С0 , A, ![]() – константы материала.
– константы материала.
Если ввести в рассмотрение линейные временные
операторы ![]()
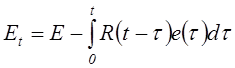 , то уравнения (4.82) и (4.83) запишутся в форме, аналогичной закону Гука
, то уравнения (4.82) и (4.83) запишутся в форме, аналогичной закону Гука
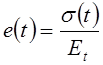 ,
, ![]() ,
(4.85)
,
(4.85)
где, как это следует из приведенной выше формулы, оператор ![]() зависит только от времени.
зависит только от времени.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.