Уравнения состояния твердого деформируемого тела. Общие принципы построения уравнений состояния. Постулат макроскопической определимости, страница 3

Под сложными моделями материала твердых тел понимаются модели, в которых учитываются два или более основных механических свойства. К числу таких моделей относятся упругопластический, вязкоупругий, вязкопластический, упруговязкопластический материал и т. д. При этом существуют разновидности этих моделей. Так, например, упругопластический материал, рис. 16 может быть представлен идеальной упругопластической моделью – а, упругопластической моделью с линейными – б и нелинейными – в упрочнениями.

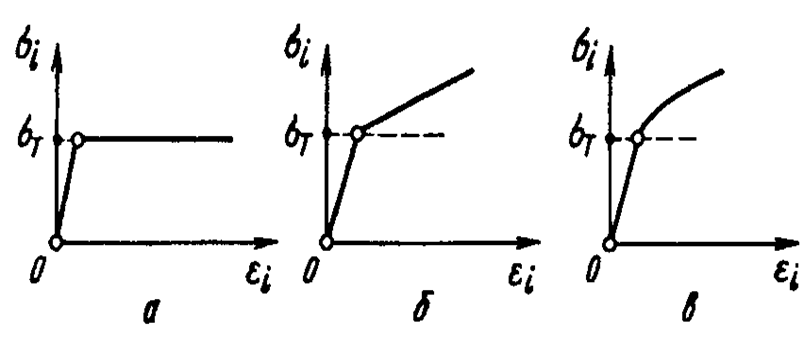
Рис. 16. Диаграммы деформирования сложных моделей материала

В механике деформируемого тела вместо реального материала рассматриваются его математические модели, отражающие основные механические свойства материала, которые имеют решающее значение для определенного класса задач. В зависимости от принятой математической модели материала механика деформируемого твердого тела подразделяется на отдельные ветви: теорию упругости, теорию пластичности, теорию ползучести, теорию вязкоупругости и т. п. Для всех перечисленных теорий геометрические уравнения, отражающие концепцию сплошности, и уравнения движения (равновесия), представляющие законы физики в сплошных средах, являются общими. Отличие теорий деформируемого тела друг от друга проявляется только в уравнениях состояния, т.е. В математических моделях материала твердого деформируемого тела.

4.2. Уравнения состояния упругого тела

Главным признаком упругого состояния материала, из которого состоит деформируемое тело, является обратимость всех процессов деформирования. Это означает, что при деформировании упругого тела отсутствует рассеивание (диссипация) энергии. При классической постановке задачи деформирования упругого тела рассматриваются только механические и тепловые виды энергии. Вследствие этого при классической постановке уравнения притока тепла в формах (3.7.4) и (3.7.6), которые в механике сплошных сред представляют собой закон сохранения энергии, в случаях малых деформаций  примут вид

                                                                     (4.5)

                                                                     (4.6)

Упругое состояние большинства твердых тел имеет место лишь при малых деформациях. Поэтому ограничение малыми деформациями для упругого деформирования является естественным.

Из термодинамики известно, что бесконечно малые изменения внутренней  и свободной  энергий являются полными дифференциалами параметров состояния. В уравнении (4.5) независимыми параметрами состояния являются компоненты тензора деформаций  и энтропия , а в уравнении (4.6) – компоненты тензора деформаций  и температура . Поэтому полные дифференциалы внутренней и свободной энергий могут быть представлены формальными выражениями

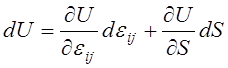              ,                                               (4.7)

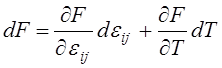              .                                               (4.8)

Сравнивая равенства (4.5), (4.6) с равенствами (4.7), (4.8), находим общие формулы представления уравнений состояния упругого тела через термодинамические потенциалы

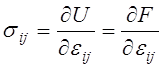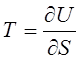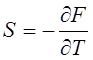     ,       ,         .                           (4.9)

Рассмотрим частные случаи деформирования упругого тела: адиабатический и изотермический процессы деформирования.

При адиабатическом процессе деформирования упругого тела нет подвода и оттока тепла, т.е. . Но поскольку в упругом теле отсутствует по определению диссипация энергии, то уравнение баланса энтропии (1.17) принимает вид

                                                                   (4.10)

Отсюда следует, что при адиабатическом процессе деформирование упругого тела , а следовательно и изменение энтропии, отнесенное к единице объема, также равно нулю, . Бесконечно малое изменение внутренней энергии упругого тела при адиабатическом процессе деформирования на основании (4.5) запишется в виде

             .                                                   (4.11)

Из формулы (4.11) следует, что при адиабатическом процессе деформирования упругого тела внутренняя энергия является потенциальной функцией компонентов тензора деформаций и носит название упругого потенциала адиабатического процесса деформирования : . Следовательно,