Уравнения состояния твердого деформируемого тела. Общие принципы построения уравнений состояния. Постулат макроскопической определимости, страница 2

            ,     .                                   (4.4)    

Из выражений (4.3) и (4.4) следует, что компоненты тензоров напряжений и деформаций являются функционалами по времени соответственно функций ,  и , , т.е. их величины зависят не только от значений соответствующих функций в момент времени t, но и от всех их предшествующих значений в момент .

Соотношения (4.3) и (4.4) определяют физические свойства вещества, из которого состоит деформируемое тело. В общем случае механическое поведение веществ зависит от направления деформации. Поэтому эти соотношения могут зависеть от принятой системы координат. Конкретизация соотношений (4.3) и (4.4) основывается на изучении физических свойств материала, из которого состоит деформируемое тело.  При этом рассматриваемые соотношения обязаны находиться в полном соответствии с началами термодинамики.

В заключение отметим, что в общем случае соотношения (4.3) и (4.4) представляют собой функциональные уравнения и их структура полностью определяется физическим строением вещества. Для упругих тел это будут дифференциальные уравнения, для вязкоупругих тел – интегродифференциальными и т.д.

4.1.3. Математические модели материала твердых тел

Основными параметрами состояния твердых деформируемых тел являются компоненты тензоров деформаций и напряжений. Из них любые шесть могут быть приняты в качестве независимых. При учете температурного воздействия на деформируемое тело вводятся дополнительные параметры состояния – температура и энтропия. Из них чаще всего за независимый параметр принимается температура. Для определения зависимости напряжений от деформаций для различных твердых материалов производят механические испытания их образцов на растяжение, сжатие и сдвиг при фиксированной температуре, см. п. 1.6. При кратковременных испытаниях зависимости напряжений для мягкой стали и хрупкого материала представлены соответственно на рис. 6 и 7. Непосредственно из этих рисунков видно, что зависимости напряжений от деформаций описываются сложными кривыми. Эти зависимости еще более осложняются при долговременных испытаниях, см. рис. 8. С другой стороны, из тех же самых рисунков видно, что существуют участки, где рассматриваемые зависимости могут быть описаны прямыми линиями или параболами. Так, например, при малых деформациях они могут быть представлены наклонными прямыми, для мягкой стали на начальном этапе текучести – прямой, параллельной оси  и т.д.

При решении практических задач часто основной интерес представляет один какой-то участок деформирования материала. Во многих случаях – это начальный участок диаграммы растяжения – сжатия материала. При решении технологических задач, связанных с формованием изделий из упругопластических материалов, наибольший интерес представляет горизонтальный участок этой диаграммы и т. д. Исходя из практических задач реальную диаграмму растяжения – сжатия материала заменяют более простой идеализированной диаграммой. Тем самым вместо реального материала используют его упрощенную математическую модель. Этим достигается упрощение решения практических задач. При грамотно выбранной математической модели достигается требуемая точность решения практической задачи.

Существуют простые и сложные математические модели материала твердых тел. Под простыми моделями понимают идеализированные представления реальных материалов, учитывающие одно из основных механических свойств. К числу простых относятся следующие две модели: модель идеально упругого материала (принимается во внимание лишь первоначальный участок диаграммы растяжения – сжатия) и модель жесткопластического материала (рассматривается только горизонтальный участок диаграммы). На рис. 15 представлены диаграммы деформирования идеально упругого – а и жесткопластического – б материалов.

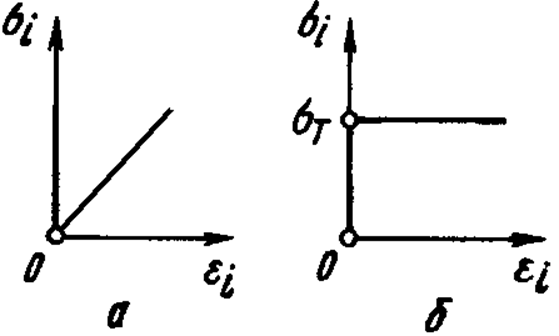
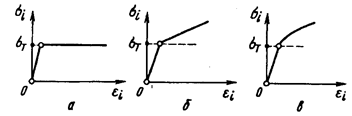
Рис.15. Диаграммы деформирования материалов