Уравнения состояния твердого деформируемого тела. Общие принципы построения уравнений состояния. Постулат макроскопической определимости, страница 4

                                                                    (4.12)

и уравнения состояния упругого тела могут быть представлены через упругий потенциал адиабатического процесса деформирования:

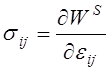              .                                                     (4.13)

Изотермический процесс деформирования упругого тела происходит при постоянной температуре  и, следовательно, . Поэтому бесконечно малое изменение свободной энергии (4.8) при изотермическом процессе деформирования упругого тела запишется в виде:

                .                                                     (4.14)

Из формулы (4.14) следует, что при изотермическом процессе деформирования упругого тела свободная энергия является потенциальной функцией компонентов тензора деформаций и называется упругим потенциалом изотермического процесса деформирования : . Следовательно,

                                                                  (4.15)

и уравнения состояния упругого тела могут быть представлены через упругий потенциал изотермического процесса деформирования:

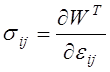               .                                                      (4.16)

Упругие потенциалы адиабатического и изотермического процессов деформирования твердых тел отличаются друг от друга незначительно. Поэтому в дальнейшем различия между ними делать не будем и обозначим их через  без верхних индексов: . Вследствие этого формулы (4.12) и (4.15) примут общую форму

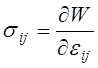               .                                                        (4.17)

В теории упругости наряду с упругим потенциалом  находит применение потенциал деформаций , который называют еще дополнительной работой деформации. Смысл последнего наименования заключается в том, что потенциал деформаций дополняет упругий потенциал до удельной работы в предположении, что в течение всего процесса деформирования компоненты тензора напряжений  сохраняют одни и те же значения, равные их окончательным величинам в положении равновесия:

.

Отсюда

и

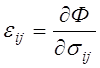                                                                             (4.18)

Потенциал деформаций представляет собой термодинамический потенциал Гиббса при изотермическом процессе деформирования. Выпишем выражение дифференциала термодинамического потенциала Гиббса (3.78) применительно к упругому телу при малых деформациях:

                .                                              (4.19)

При изотермическом процессе деформирования  и , а, следовательно, потенциал деформаций действительно представляет собой термодинамический потенциал Гиббса при изотермическом процессе деформирования упругого тела, .

Определяя упругий потенциал  или потенциал деформаций  различным физически обоснованным способом и придавая им допустимые условиями взаимодействия с внешней средой приближенные значения, можно строить различные модели упругого тела [9].

4.3. Закон Гука

4.3.1. Общая форма записи закона Гука

Опыт показывает, что напряжения и деформации во многих деформируемых телах при невысоких уровнях деформаций и температур связаны линейной зависимостью, которая носит название закона Гука. Предположим, что эти условия соблюдены и производные  могут быть разложены в ряд Тейлора в окрестности естественного состояния тела, т.е. состояния при котором отсутствует воздействие на рассматриваемое тело внешних сил и физических полей. Рассматривая появление деформаций и напряжений в сплошном теле, как его реакцию на внешние воздействия, примем, что при естественном состоянии деформации,  и напряжения, . При этом следует отдавать себе отчет в том, что в реальном теле могут существовать начальные деформации и напряжения, которые могут возникать в процессе его изготовления. Если последние известны, то они могут быть учтены после решения задачи воздействия на рассматриваемое тело внешней среды путем алгебраического сложения с полученным результатом решения.

Ограничиваясь первыми двумя членами разложения производных в ряд Тейлора в окрестности естественного состояния тела, получим на основании формулы (4.17) следующее выражение