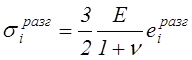, см. формулу (4.33).
Отсюда
вытекает следующая расчетная схема определения остаточных напряжении 
и деформации 
, которые образовались в
теле в результате его первоначального нагружения объемными 
и поверхностными 
силами за пределы упругости
и последующего уменьшения этих сил до значений 
и
. Сначала решается
упруго-пластическая задача и для уровня внешних нагрузок и , определяются напряжения 
и деформации 
. Затем для внешних нагрузок
и 
решается упругая задача,
при которой определяются напряжения и деформации разгрузки: 
, 
.
Тогда
, 
.
При этом предполагается, что в процессе разгрузки материал не выходит вновь за пределы упругости.
Главным признаком состояния ползучести материала является рост деформаций при постоянном напряжении. В состоянии ползучести при постоянной деформации происходит уменьшение напряжений. Это явление называется релаксацией напряжений. Некоторые материалы, такие как пластмассы и бетон, могут находиться в состоянии ползучести при комнатной температуре. Конструкционные металлы переходят в состояние ползучести в основном только при повышенных температурах. Явление ползучести является более сложным, чем упругость и пластичность. В отличие от упругого и пластического состояния ползучесть представляет собой процесс протекающий во времени. Поэтому в уравнения состояния ползучести обязательно входит время. Для различных материалов разрабатываются свои теории ползучести. Эта отрасль механики деформируемого твердого тела еще далека до своего завершения. Здесь рассматриваются общие подходы к построению уравнений состояния и некоторые уравнения состояния, характерные для металлов. Подробное изложение явления ползучести изучается в курсе теории ползучести.
При установлении зависимости между компонентами тензоров напряжений и деформаций в механике деформируемого твердого тела большую роль играет эксперимент. Одной из основных задач экспериментального исследования явления ползучести является построение кривых ползучести. Типичная кривая ползучести, полученная в результате растяжения металлического образца, приведена на рис. 23. Кривые ползучести строятся при постоянных напряжениях и температурах в условиях линейного напряженного состояния. С повышением температуры и уровня напряжений явление ползучести для большинства конструкционных материалов резко усиливается. Для некоторых материалов, таких как алюминиевые и титановые сплавы, стеклопластики, ползучесть проявляется при обычной температуре. Следует заметить, что даже при линейном напряженном состоянии зависимость между деформацией ползучести, напряжением, скоростями их изменения и временем весьма сложная. Поэтому и в этом простейшем случае приходится прибегать к упрощающим предположениям.
 |
При исследовании напряженно-деформированного состояния любой детали сооружения, работающей в условиях ползучести, наибольший интерес представляют первая и вторая стадии ползучести, см. рис. 23. Это объясняется тем, что эксплуатация деталей обычно осуществляется в интервале времени, соответствующим этим двум стадиям. На третьей стадии происходит уже разрушение. На основании исследования кривых ползучести были предложены различные уравнения, отражающие первую и вторую стадии кривых ползучести. Они могут быть разбиты на две группы.
Первая группа уравнений основывается на предположении, что кривые ползучести при различных напряжениях и одинаковых температурных геометрически подобны:
,
(4.70)
где 
– деформация
ползучести, g – функция
напряжения и температуры, W – функция времени
и температуры.
При построении второй группы уравнений принимается, что деформация ползучести может быть представлена в виде суммы:
,
(4.71)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.