Уравнения состояния твердого деформируемого тела. Общие принципы построения уравнений состояния. Постулат макроскопической определимости, страница 10

Впервые условие начала пластичности (4.53) было установлено экспериментальным путем в 1868 г. французским инженером Треска. Сен-Венан дал математическую формулировку этого условия для плоской задачи. С физической точки зрения условие (4.53) означает, что при сложном напряженном состоянии начало образования пластических деформаций происходит при условии, когда наибольшие касательные напряжения достигнут предела текучести при чистом сдвиге. Условие (4.53) называют условием наибольших касательных напряжений или условием Треска-Сен-Венана. Недостатком этого условия является пренебрежение промежуточным главным напряжением .

Уравнения (4.51) позволяют условие начала пластичности представить в виде

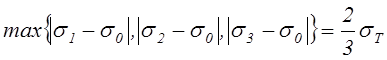               .                            (4.54)

Это условие впервые было предложено А. Ю. Ишлинским. Его называют условием наибольшего приведенного напряжения.

Уравнение (4.52) в качестве условия начала пластичности было вначале предложено Максвеллом, а затем Хубером на основе рассмотрения потенциальной энергии формоизменения. Его называют энергетическим условием начала пластичности, а иногда условием начала пластичности Хубера-Мизеса.

Согласно формуле (3.33) энергетическое условие начала пластичности (4.52) можно представить в виде

         ,                                                           (4.55)

где  – интенсивность напряжений (3.33).

Известные результаты экспериментальных исследований лучше всего согласуются с энергетическим условием (4.55). Поэтому это условие и получило наибольшее распространение в теории пластичности.

4.4.2. Поверхность пластичности

В случае линейного напряженного состояния пластические деформации растяжения или сжатия возникают при достижении предела текучести , который на диаграмме растяжения, см. рис. 19, обозначен точкой B. В теории пластичности пределы пропорциональности и упругости считаются совпадающими с пределом текучести. Это не вносит существенной ошибки в теорию, так как все три рассматриваемых предела у конструкционных материалов находятся вблизи друг друга.

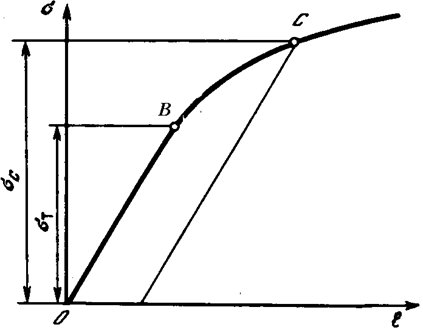
Рис.19. Диаграмма растяжения

При деформировании материала за пределом текучести при отсутствии площадки текучести происходит упрочнение материала, что равносильно увеличению предела текучести. Так, если деформирование продолжается до точки С, см. рис. 19, то предел текучести увеличивается до . Теперь при нагружении от 0 до  соблюдается закон Гука. При увеличении напряжения сверх  материал деформируется упруго-пластически. Поэтому напряжение  можно считать текущим пределом текучести, который разграничивает упругую и пластическую деформации.

Для разграничения упругого и пластического деформирования упрочняющегося материала в случае сложного напряженного состояния вводится условие пластичности

,                                                       (4.56)

которое отличается от условия начала пластичности (4.48) тем, что в него дополнительно входит мера упрочнения. В качестве меры упрочнения q, обычно принимают работу пластической деформации

               ,                                                     (4.57)

или параметр Удквиста

                .                                                        (4.58)

В равенствах (4.57) и (4.58) интегралы берутся по пути деформирования. Мера упрочнения (4.57) основывается на предположении, что упрочнение материала определяется только работой, затраченной на необратимую пластическую деформацию. Параметр Удквиста (4.58) основан на предположении, что упрочнение определяется накопленной пластической деформацией. Расчеты показывают, что обе эти меры упрочнения в случае энергетического условия пластичности для изотропного материала приводят к одинаковым результатам.

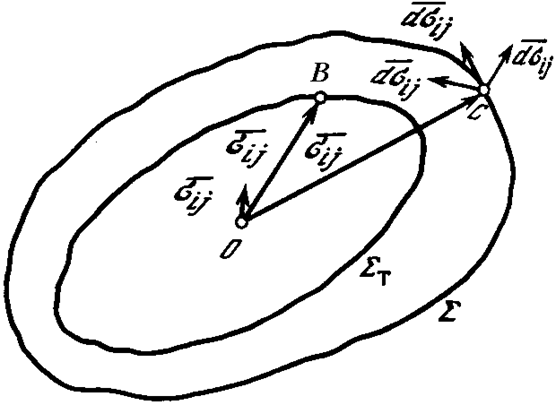Рис. 20. Поверхности пластичности и начала пластичности

Уравнение (4 .56) является уравнением гиперповерхности пластичности S в шестимерном пространстве компонентов напряженного состояния, которая разделяет области упругого и пластического деформирования. Как и поверхность начала пластичности S_Т, она может быть изображена в трехмерном пространстве главных напряжений. На рис. 20 показаны поверхности начала пластичности S_Т и S и напряжения, соответствующие точкам B и С на диаграмме растяжения, представленной на рис. 19.