До сих пор предполагалось, что температура тела и окружающей его среды постоянна и одинакова для всех точек тела. Поэтому она исключалась из рассмотрения. Однако хорошо известен следующий опытный факт: при нагревании любое тело расширяется, а при охлаждении сжимается. Более того, и само деформирование твердого тела может вызвать изменение температуры. Строго говоря, учет температуры должен вестись на основе совместного решения уравнений теории упругости и теплопроводности. Однако связанность полей деформации и температуры слабая, и результаты, получаемые при совместном и раздельном решении указанных уравнений, отличаются незначительно. Поэтому здесь ограничимся лишь изменениями, которые вносит температура в уравнения закона Гука. Это, так называемая несвязная задача термоупругости. Если уравнения теории упругости решаются совместно с уравнениями теплопроводности, то такая задача носит название связанной задачи термоупругости.
Экспериментальным
путем установлено, что в случае отсутствия препятствий при изменении
температуры однородного тела от 
до 
в
нем возникают температурные деформации, не вызывающие напряжений. Это
обстоятельство полностью подтверждается строгим термодинамическим анализом. В
результате деформации упругого тела находятся суммированием упругих и
температурных составляющих, а уравнения состояния упругого тела с учетом
температуры записываются в виде
, (4.34)
где 
– коэффициенты
температурного расширения. Уравнения (4.34) носят название закона Дюгамеля -
Неймана. Применительно к изотропному материалу они преобразуются к виду
,
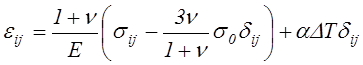(4.35)
где 
– компоненты шарового
тензора напряжений, 
– символ Кронекера.
В общем случае коэффициенты упругой податливости и модули упругости материала зависят от температуры, но при малых изменениях температуры эта зависимость настолько слабая, что ею обычно пренебрегают. Температура в общем случае зависит не только от координат точек тела, но и от времени и должна удовлетворять уравнениям теплопроводности. В результате возникает сопряженная задача термоупругости, когда приходится решать уравнения теории упругости совместно с уравнениями теплопроводности. При статическом воздействии температурного поля задача термоупругости разделяется: сначала находится температура во всех точках тела, а затем решаются уравнения теории упругости с использованием уравнений закона Дюгамеля – Неймана.
Следует отметить, что взаимодействие упругих и температурных полей – это не единственная задача, изучающая сопряженные физические процессы на базе теории упругости. Широко исследуются вопросы сопряжения упругих полей с электрическими (электроупругость), магнитными (магнитоупругость), гидравлическими (гидроупругость) и другими видами физических полей.
У некоторых материалов типа резины и пластмасс, а также таких металлов, как чугун и медь, наблюдаются существенные отклонения свойств упругости от линейного закона. Для формулировки законов нелинейной упругости обычно используется определенная форма упругого потенциала W, поскольку с помощью равенства (4.17) в этом случае легко устанавливается зависимость между компонентами тензоров напряжений и деформаций. У различных классов материала проявляются свои особенности нелинейной упругости, в связи с чем существуют различные формулировки закона упругости.
В основу уравнений состояния нелинейной упругости можно положить упругий потенциал W, который, как это было выяснено в п.4.2, имеет строгое термодинамическое обоснование. Упругий потенциал W не зависит от принятой системы координат и может быть представлен в виде функции шести компонентов тензора деформаций, см. (4.17). Отсюда следует, что он может рассматриваться и как функция трех инвариантов тензора деформаций
.
(4.36)
Из представления упругого потенциала в форме (4.36) имеем, что
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.