Уравнения состояния твердого деформируемого тела. Общие принципы построения уравнений состояния. Постулат макроскопической определимости, страница 16

В случае одноосного растяжения при пренебрежении неизменяемостью объема материала в условиях ползучести ,  ,  . Так как , то функция F₁ может быть определена по кривой ползучести, поскольку производная  в каждый момент времени t₁ равна тангенсу угла наклона касательной к кривой ползучести с временной осью, tga на рис. 26. Поэтому

.

Рис.26. К определению функции F₁ по tg a

Если использовать условие подобия кривых ползучести, то на основании сопоставления равенств (4.73) и (4.77) имеем

, так как , .

При вычислении скоростей компонентов полной деформации считается возможным использовать принцип суперпозиции:

, где просуммированы составляющие скоростей деформации упругости, пластичности и ползучести. Принимая во внимание, что при определении функции  по кривым ползучести используется суммарная деформация образца, то  и . В результате зависимость скоростей компонентов деформации от компонентов тензора напряжений принимает вид

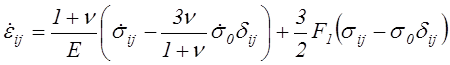                                             (4.78)

где ,  – скорости изменения компонентов тензора напряжения.

Уравнения (4.78) являются основными уравнениями теории течения в условиях ползучести. Теория течения удовлетворительно описывает явление ползучести при достаточно больших напряжениях, которые во времени являются постоянными, либо достаточно медленно изменяющимися.

4.5.4. Теория старения

В теории старения предполагается, что для любого напряженного состояния является справедливой определенная зависимость между интенсивностью деформации ползучести  и интенсивностью напряжений

, где функция  определяется из опытов на одноосное растяжение при  и имеет геометрический смысл величины обратной составляющей секущего модуля, определяемой деформациями ползучести, см. рис. 27.

.

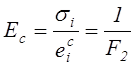Применив ассоциированный закон течения (4.62) к деформациям ползучести и те соображения, которые использовались при выводе зависимости (4.76), получим

.

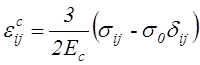Прибавив сюда упруго-пластические деформации (4.69) , получим

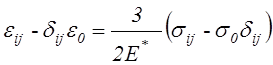                   ,                                    (4.79)

где

.

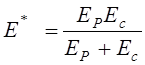Здесь  и  определяются при одноосном растяжении соответственно из диаграммы деформирования при кратковременной нагрузке и по кривым ползучести.

Рис. 27. К определению функции F₂ по tg a

Уравнения (4.79) являются основными уравнениями теории старения в условиях ползучести.

Теория старения применима при постоянных или слабоизменяющихся нагрузках.

4.5.5. Теория упрочнения

В теории упрочнения основой является предположение о том, что скорость интенсивности деформаций ползучести является функцией интенсивности напряжения и интенсивности деформаций ползучести

             ,                                                   (4.80)

где функция  часто принимается в виде

.

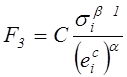Здесь коэффициенты С, a, b находятся из опыта на одноосное растяжение, имея в виду, что интегрирование (4.80) при  дает следующее выражение

Так как , то на основании зависимости (4.76) имеем

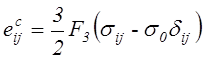
и основные уравнения теории упрочнения по форме оказываются совпадающими с уравнениями теории течения (4.78):

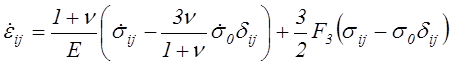                                               (4.81)

Уравнения (4.81) являются основными уравнениями теории упрочнения в условиях ползучести. Теория упрочнения правильно характеризует ряд особенностей явления ползучести при изменяющихся нагрузках. При не очень сложных путях нагружения теория упрочнения удовлетворительно описывает ползучесть металлургически стабильных металлов и сплавов.

4.6. Уравнения состояния наследственной теории ползучести

4.6.1. Особенности ползучести неметаллических материалов

При ползучести неметаллических конструкционных материалов, таких как древесина, бетон, стекло-, угле-, боропластики наблюдаются следующие особенности:

- линейная зависимость деформаций ползучести от напряжений в диапазоне допускаемых условиями эксплуатации сравнительно небольших уровней последних;

- отсутствие стадии установившейся ползучести;

-упругое последействие при снятии нагрузки и отсутствие остаточных деформаций в области линейной ползучести для структурно устойчивых материалов;