Уравнения состояния твердого деформируемого тела. Общие принципы построения уравнений состояния. Постулат макроскопической определимости, страница 15

где g₁ и g₂ – функции напряжения и температуры, а Y – монотонно и быстро убывающая функция времени. При  из (4.71) следует зависимость (4.70). Отсюда ясно, что зависимость (4.70) является частным случаем более общей формулы (4.71). Однако зависимость (4.70) является более простой и, как показывают расчеты, обладает вполне достаточной точностью. Поэтому она нашла широкое применение на практике, особенно в форме

                   ,                                                 (4.72)

где функция W обычно не аппроксимируется аналитическими зависимостями, так как выполнение расчетов ползучести возможно и без этого. Формула (4.72) хорошо согласуется с опытными данными. Заметим, что при t = 0  W= 0 , так как в этом случае .

Если выражение (4.72) продифференцировать по времени, то получим зависимость скорости ползучести  от напряжения и температуры

                                                                       (4.73)

где

.

Рис.24. Графики функции W и В

На рис. 24 представлен типовой вид графиков функций W и В. Величины a и k, показанные на рис. 24, характеризуют функции W и B во второй стадии ползучести:

,          .

Если в условиях ползучести в какой-то момент времени t₁ произошла разгрузка, то деформация начинает изменяться. Причем в момент разгрузки деформация уменьшается скачком на величину упругой составляющей s/E, а затем происходит ее постепенное уменьшение, см. рис. 25. Это явление называется восстановлением или обратной ползучестью. У металлов восстанавливается только часть деформации, накопленной в период нагрузки. У неметаллических материалов может восстанавливаться вся деформация, так называемое явление

упругого последействия.

Рис.25. Графики деформирования при нагружении и разгрузке

Рассмотренные кривые ползучести при линейном напряженном состоянии являются основой расчетов на ползучесть.

4.5.2. Понятие о технических теориях ползучести

В настоящее время наибольшее распространение получили три технические теории ползучести: течения, старения и упрочнения. Они основываются на экспериментально проверенных предположениях о наличии функциональной зависимости между деформациями, напряжениями, скоростями их изменения и времени. При переходе от одноосного (линейного) напряженного состояния к сложному считается возможным применить основные гипотезы теории пластичности. Это обосновывается тем, что деформации ползучести являются в основном необратимыми.

Аналогично ассоциированному закону течения предполагается, что компоненты скоростей деформации ползучести определяются формулой

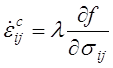     ,                                                     (4.74)

где  – функция ползучести.

Подставив компоненты скоростей деформаций ползучести (4.74) в выражение для интенсивности скоростей деформаций, получим

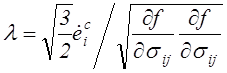.                                         (4.75)

При ползучести, как и в случае пластичности, пренебрегают изменением объема материала, т.е.  или . Это позволяет определять функцию ползучести  на основе энергетического критерия формоизменения. Тогда, также как в п. 4.4.5, в случае изотропного упрочнения имеем

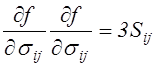
и

.

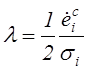В результате зависимости компонентов скоростей деформации ползучести от компонентов тензора девиатора напряжений принимают вид

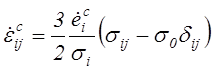.                                         (4.76)

Далее, предполагая, что интенсивности скоростей деформации ползучести и напряжений не зависят от вида напряженного состояния, строятся на основании различного рода допущениях о связях между напряжениями, деформациями и скоростями различные теории ползучести.

4.5.3. Теория течения

В теории течения предполагается, что независимо от вида напряженного состояния существует определенная связь между интенсивностью скоростей деформации ползучести и интенсивностью напряжений

         ,                                                   (4.77)

где функция  определяется из опытов на одноосное растяжение при .