Изучение численных методов инженерных расчётов и сопутствующего математического аппарата, применяемых при решении задач механики

Можно разбить матрицу на клетки – так называемым окаймлением, то есть выделяем матрицу размерности (n– 1) и последние строку и столбец.

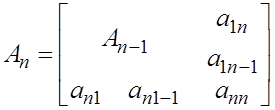
Действия над окаймленными матрицами проводят как действия над клеточными.

Рассмотрим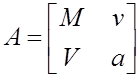     

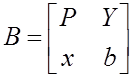
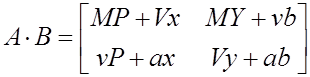
Обращение матриц

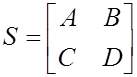       клеточная

 и  - квадратные,  p+ q= n

Найдем 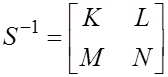  , где

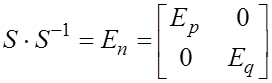
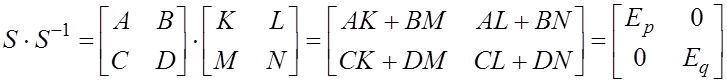
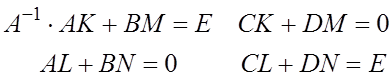
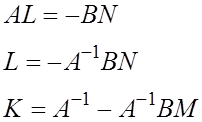
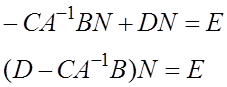
1)

2)

3)

4)

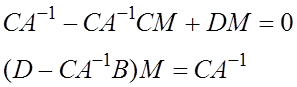
5)

1) – 4) – вычисления начинаются с

Вторая группа (обращение начинается с )

                      

    

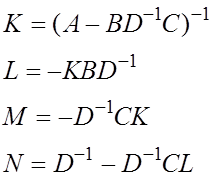
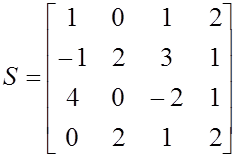
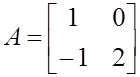
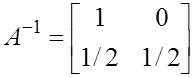
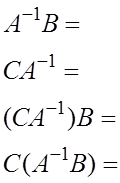
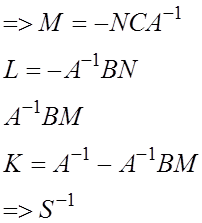
Треугольные матрицы. Разложение матрицы на произведение 2-х треугольных матриц.

Матрица: нижняя треугольная е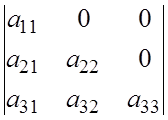сли , если

верхняя треугольная, если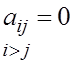

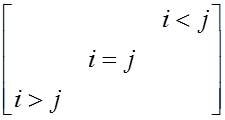
Определитель треугольной матрицы равен произведению ее диагональных элементов.

Обратная матрица неособенной треугольной матрицы также треугольная матрица того же ранга и структуры.

Матрица обратная к левой треугольной – является левой, обратная к правой – правой треугольной.

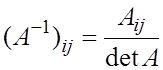 (алгебраическое дополнение ненулевых элементов треугольной матрицы равно 0)

        

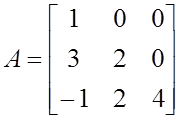
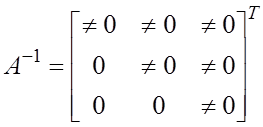
Теорема. Если квадратичная матрица имеет отличные от нуля диагональные матрицы ,  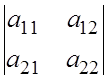и так далее, не равны нулю, то ее можно разложить на произведение 2-х треугольных матриц (верхней и нижней). Это разложение будет единственным, если задать диагональные элементы одной из матриц (например, положить их равными единице)

         

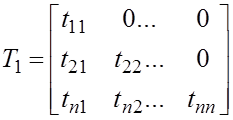
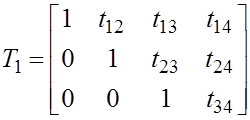
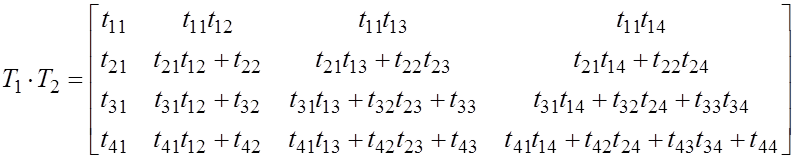
приравниваем соответствующие элементы матриц

                   

 ,

               

   

                       

                           

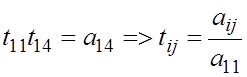
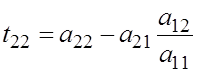
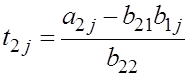
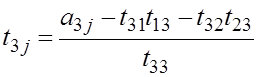
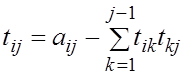
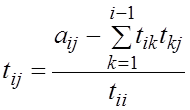
Решаем последовательно двухчленные, трехчленные уравнения и получаем  и

Обратим матрицу, которая представлена произведением двух треугольных.

         

             

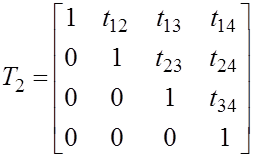
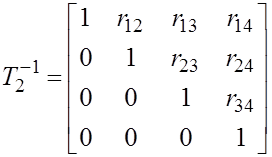
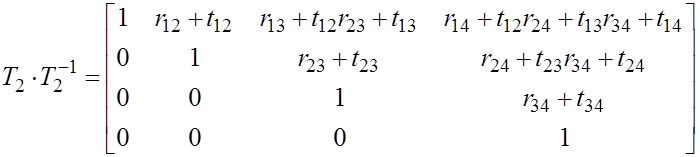
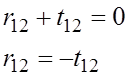
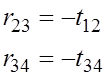
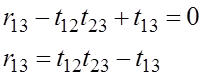
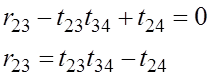
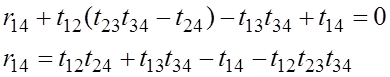
Аналогично обращается , на практике возможно даже не 0.

Это разложение называется LU разложение

Требования теоремы (не равенство нулю соответствующих миноров) заведомо выполняется для матриц с диагональным преобладанием, то есть

 

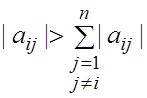
Решение СЛАУ с помощью LU – разложения

                                                                                                                          (1)

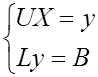   равенство можно записать в виде системы

Тогда решение СЛАУ (1) с квадратной матрицей сводится к решению 2-х систем с треугольной матрицей

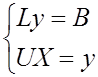
     вектор вспомогательных переменных

Сначала находим , потом х как обратный ход метод Гаусса.

     

        

        

     

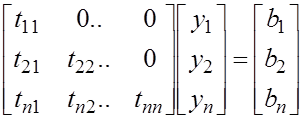
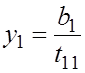
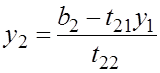
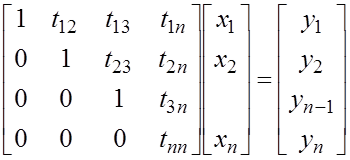
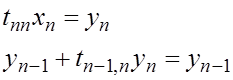
LU – разложение, есть преобразование системы к треугольной по методу Гаусса т.е. это другая реализация метода Гаусса.

LU разложения – называются  еще схемой Халецкого (1875-1918) – французский математик-геодезист.

Иногда схемой Халецкого называют способ решения симметричных линейных систем (метод квадратных корней)

Итерационные методы

1)  метод простой итерации

Система                                                                                                                   (1)

преобразуется к виду                                                                                                                  (2)

строится последовательность  векторов (столбцов)

 - произвольный,    

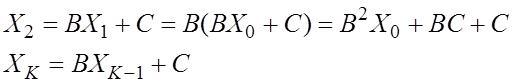
если последовательность матриц-столбцов  сходится к решению системы, то говорят, что метод итерации сходится

Предварительно докажем Лемму 1:

Для того, чтобы  необходимо и достаточно, чтобы все собственные числа матрицы А были бы .

Достаточно что:      - собств.числа матрицы В

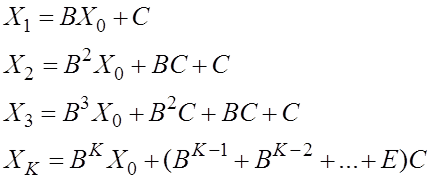
Получается ряд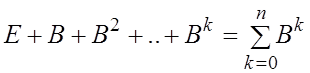

Покажем, что Лемма (2) если  , то ряд сходится и при этом

      

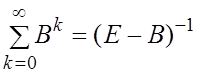
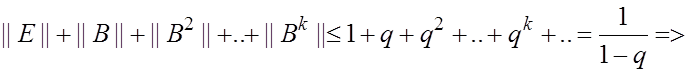
Матричный ряд

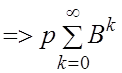- сходится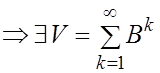

                 

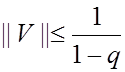
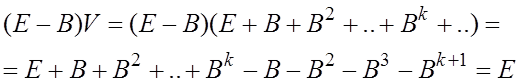
Лемма 1.  необходимо и достаточно чтобы

1)

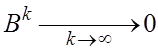
2)  - имеет обратную и

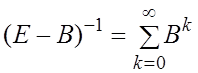
Лемма 2. ]  матрица 

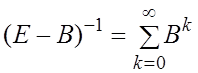
Теорема: необходимо и достаточно условие сходимости метода простых итераций при любом начальном векторе  является все собственные числа матрицы В д.б.

Достаточность: 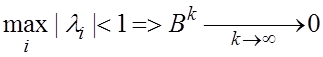 и

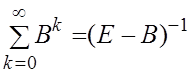 – эта матрица является суммой ряда, т.е.пределом частных сумм.

           

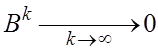
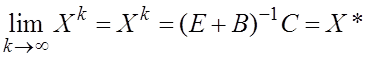 при любом

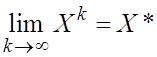
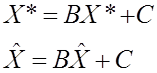
     является собственным числом, что противоречит условию.

Необходимость:

Теорема 2. ] , тогда при любом  получившийся улучшенный метод простых итераций сходится к единственному  решению и любому к верен оценки для погрешности.

1) 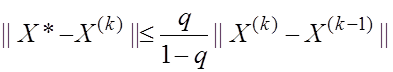         апостериорное

2) 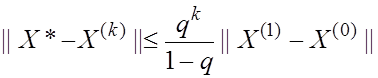  априорное

Априорная оценка как правило грубее апостериорной.

Априорная оценка позволяет подсчитать заранее число итераций достаточное для получения  с заданной точностью  при выбранном начальном вектором . Для этого нужно найти наименьшее целое решение неравенства.

Относительно              

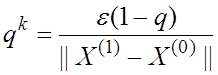
так как             

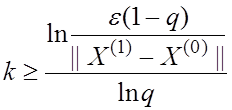
Апостериорной оценкой удобно пользоваться, непосредственно в процессе вычислений и останавливать этот процесс, как только выполнится неравенство.

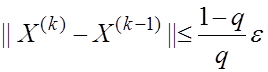
Отметим, что неравенство

 будет гороилей того, что  только если

Обычно за  принимают вектор С – свободных членов системы, если неизвестно какое-нибудь близкое решение.

если , то априорная оценка

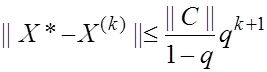 любое

Дополнительный процесс итераций сходится, если все элементы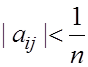  

n – число неизвестных.

Метод Якоби.

(1)         приведем к виду

(2)    

После выясним, каким условиям удовлетворяет матрица В, то есть для сходимости трег.  для В, следует выяснить как приведем (1) к (2) чтобы условие сходимости выполнилось.

Представим матрицу  , где  - диагональная,  и  – левая и правая строи треугольной (т.е. нулевой диагональю) матрицы.

И если на диагонали исходной матрицы нет нулей: то эквивалентной (1) задачи вида (2) будет

                                                                       (3)

то есть               

Метод простых итераций основанный на этом произведении систем