Исследование напряженно-деформированного состояния однородной цилиндрической оболочки при действии бокового давления

Министерство образования и науки Российской Федерации

Дальневосточный федеральный университет

Естественно-научный институт

Механико-математический факультет

Кафедра прикладной математики и механики

УТВЕРЖДАЮ

Зав. кафедрой ПМиМ

к.ф.-м.н., доцент

  __________

«___» ________ 20     г.

Выпускная работа на тему:

«Исследование напряженно-деформированного состояния однородной цилиндрической оболочки при действии бокового давления»

Исполнитель        ____________      «20» июня 2011г.

Руководитель       ____________      «20» июня 2011 г.

Содержание.

1.  Введение ----------------------------------------------------------------------------- 3

2.  Постановка задачи ------------------------------------------------------------------4

3.  Математическая модель -----------------------------------------------------------5

4.  Вывод фундаментальных уравнений -------------------------------------------9

5.  Численное решение (реализация в программе Maple) ---------------------13

6.  Реализация в программе Ansys и сравнение результатов -----------------17

7.  Вывод --------------------------------------------------------------------------------18

8.  Приложение ------------------------------------------------------------------------19

9.  Список литературы ---------------------------------------------------------------35

Введение.

Тонкостенные элементы в виде оболочек широко применяются в различных отраслях современной техники. Интерес к такого рода объектам объясняется тем, что оболочки обладают весьма выгодными упругими свойствами и при рациональном проектировании могут выдержать значительные нагрузки при минимальной толщине. В этом отношении они гораздо выгоднее пластин и плоских перекрытий и дают конструктору примерно те же преимущества, что при замене балок арками. Данное свойство оболочек позволяет создать из них конструкции весьма легкие при достаточной прочности и способствует широкому применению подобных конструкций в судостроении, самолетостроении, словом, везде, где малый вес является необходимым.

Постановка  задачи.

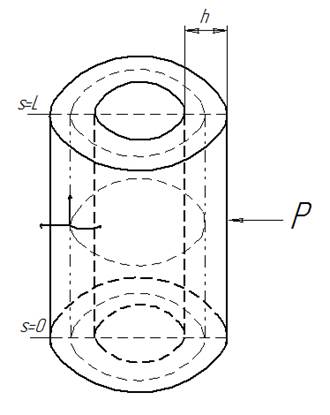
Дана цилиндрическая оболочка конечной длины  L, постоянной толщины h. Рассматриваем осесимметричную задачу, не зависимую от угла φ.

Оболочка закреплена на двух концах и к ней приложено боковое равномерно распределённое напряжение . Нам требуется определить её напряжённо деформированное состояние. Основная координатная поверхность совмещается со срединной поверхностью оболочки.

Математическая модель.

Физическая состоятельная теории оболочек была разработана профессором Владимиром Васильевичем Пикулем.

Для построения фундаментальных уравнений мы используем уравнения равновесия, уравнения геометрии и закон Гука в ортогональной криволинейной системе координат при осесимметричном деформировании.

Уравнения равновесия:

             

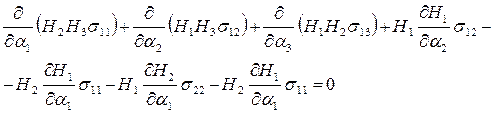
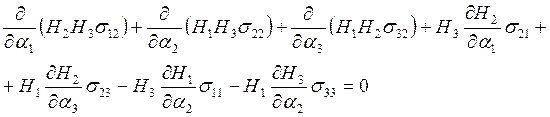
(1)

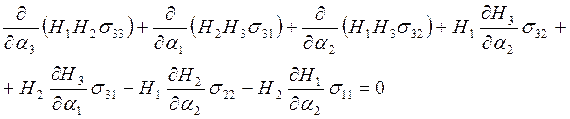
В качестве  мы берём  т.к. в теории оболочек используется цилиндрическая система координат, где     .

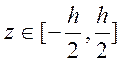Учитывая, что зависимость от угла уходит, и применяя коэффициенты Ламе для цилиндрической системы координат: H₁=H₃=1 ₂=R+z, мы получаем уравнения равновесия в оссесимметричном случае. Стоит отметить, что второе уравнение равновесия полностью пропадает.

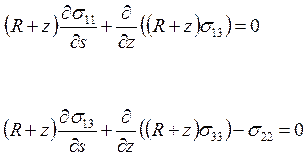
                                                                 (2)

Аналогично мы поступаем с уравнениями геометрии.

 

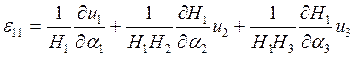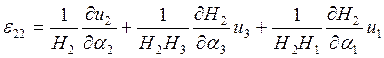(3)

 

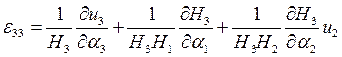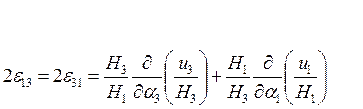
Для получения осессиметричных уравнений геометрии мы также сократили коэффициенты зависящие от угла, и применив коэффициенты Ламе для цилиндрической системы координат получили:

 

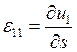                                        (4)

 

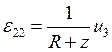                                          (5)

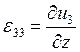                                           (6)

 

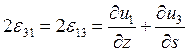                                                (7)

Так же в работе для построения фундаментальных уравнений мы использовали уравнения Гука для изотропного материала.

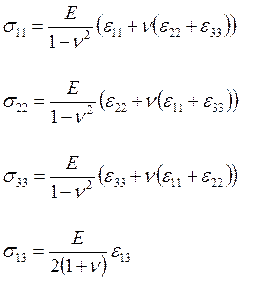
                                                                       (8)

Гипотезы применяемые в работе.

На ряду с основными уравнениями  мы используем гипотезы которые мы применяли в нашей работе для реализации задачи и вывода фундаментальных уравнений .

1) Расчёт оболочки можно с достаточной точностью вести на основе теории тонких упругих оболочек на основе с использованием гипотез Кирхгоффа- Тимошенко, которые сводятся к условиям:

·   

Напряжение   считается равным нулю в законе Гука, т.е. закон Гука берётся как для плоского случая.

· 

Деформация по толщине равна нулю.

· 

Касательная деформация применяется в виде одномерной функции.

2) В силу осевой симметрии некоторые компоненты тензора деформации и перемещение обращаются в ноль.

 

Реализация.

Вывод фундаментальных уравнений.