Основные уравнения нелинейно-упругого и упруго-пластического тела. Уравнения равновесия. Уравнения изменения формы и изменения объема тела

2.3. Основные уравнения нелинейно-упругого и упруго-пластического тела

2.3.1. Уравнения равновесия

2.3.2. Граничные условия (ГУ)

2.3.3. Геометрические уравнения

2.3.4. Уравнения совместности

2.3.5. Реологическое уравнение состояния тела

2.3.6. Уравнения изменения формы и изменения объема тела

2.3.1. Уравнения равновесия

Эти уравнения имеют вид

;

  ;  (2.19)

, где X,Y,Z– проекции объемных сил.

2.3.2. Граничные условия (ГУ)

Граничные условия могут быть статическими, кинематическими и смешанными.

Статические ГУ имеют вид

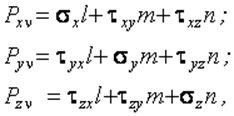   (2.20)

где l,m,n– направляющие косинусы;  – проекции внешних сил.

Если заданы компоненты смещений, то такие ГУ называют кинематическими. Если заданы одновременно компоненты перемещений и напряжений, то условия называют смешанными.

2.3.3. Геометрические уравнения

Эти уравнения обычно называют уравнениями Коши:

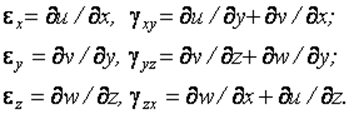   (2.21) 

2.3.4. Уравнения совместности

Эти уравнения имеют вид

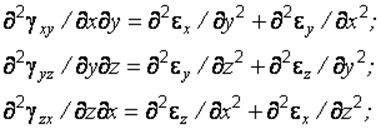
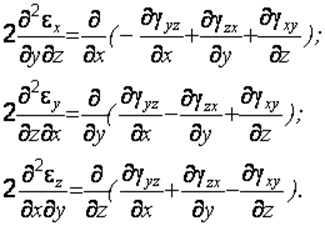   (2.22)

2.3.5. Реологическое уравнение состояния тела

При рассмотрении процессов, протекающих во времени, в уравнения состояния необходимо включить время (в явной или неявной форме). Такое уравнение называют реологическим уравнением состояния. Оно связывает между собой тензоры напряжений , деформаций , скорости нагружения , скорости деформации  и время :

   (2.23) 

В итоге имеем 3 уравнения равновесия, 6 уравнений совместности (неразрывности) деформаций и 6 уравнений состояния. Уравнения равновесия являются статическими уравнениями механики сплошной среды, справедливыми для любой точки материального тела. Уравнения совместности деформаций являются геометрическими уравнениями механики сплошной среды. Они отображают условие, при котором рассматриваемое тело является непрерывным, сплошным и остается таковым после деформации. Уравнения состояния отображают (макроскопически) физические свойства тела.

2.3.6. Уравнения изменения формы и изменения объема тела

При рассмотрении процесса деформирования тела подразделяют изменение формы этого тела , связываемое с интенсивностью касательных напряжений , и изменение объема тела , проявляющееся под воздействием среднего нормального (всестороннего) давления , причем изменения формы и объема могут описываться различными законами. В классической теории упругости и пластичности справедливы закон изменения объема

   (2.24)

и закон изменения формы

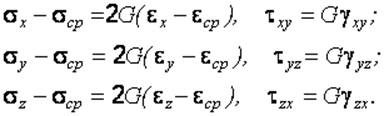   (2.25)

В формулах (2.24, 2.25) объемный модуль K определяет сопротивление материала при изменении объема, а модуль сдвига G – при изменении его формы.

2.4.Простое и сложное нагружение

Характер нагружения оказывает существенное влияние на напряженно-деформированное состояние тела. Простым нагружением, по А.А. Ильюшину [17, 18], называют такое, при котором компоненты девиатора напряжений  возрастают пропорционально одному параметру. Если это условие не соблюдено, то нагружение называют сложным.

Если напряженное состояние тела однородно (что возможно при неучете массовых сил), то при возрастании внешних сил пропорционально одному параметру β нагружение будет простым. Так, при возрастании нагрузок по закону βР все компоненты девиатора напряжений возрастают пропорционально множителю β. Параметр β может быть временем, т. е. положение о простом нагружении справедливо и для возрастания нагрузки во времени.

Простое нагружение, как показал А.А. Ильюшин, возможно при степенном законе связи между интенсивностями напряжений и деформаций  (при условии несжимаемости). Но такое нагружение может иметь место и при других видах нелинейной связи между напряжениями и деформациями.

В целом условие простого нагружения существенно упрощает решение задач.

2.5.Активная и пассивная деформации

Различают активную деформацию, возникающую в процессе нагружения тела, и пассивную, развивающуюся при разгрузке. Для простых напряженных состояний эти понятия являются достаточно определенными. При сложном напряженном состоянии деформацию в каждый данный момент времени называют активной, если интенсивность напряжений  в этот момент превышает все предшествующие ее значения. Если интенсивность напряжений  меньше, хотя бы одного ее предшествующего значения, деформацию называют пассивной [16]. При активном деформировании возрастает как упругая, так и пластическая часть деформации, при пассивном же деформировании пластическая часть остается постоянной, а упругая уменьшается.