Основные уравнения нелинейно-упругого и упруго-пластического тела. Уравнения равновесия. Уравнения изменения формы и изменения объема тела, страница 3

 

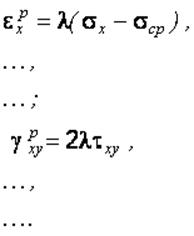
2.6.5. Разгрузка

При разгрузке тела интенсивность деформаций убывает (рис. 1.3, б):

 

где  – деформация разгрузки  – остаточная деформация.

Принимают, что в процессе разгрузки уменьшение интенсивности деформаций прямо пропорционально уменьшению интенсивности напряжений, т. е.  Соответственно для процесса разгрузки справедливы соотношения (2.35).

2.6.6. Теория пластического течения

В этой теории, развитой Прандтлем и Рейсом, приращения деформаций рассматриваются как сумма приращений упругих (e) и пластических (p) деформаций:

    (2.38)

Приращения упругих деформаций будут соответственно равны

   (2.39)

а приращение пластических деформаций

   (2.40)

Соотношения (2.39) и (2.40) представляют собой формулировку допущения 1 о том, что приращение деформаций есть функция интенсивности напряжений, а приращение деформаций объема – функция среднего нормального напряжения; причем принимают, что объемные изменения являются упругими и прямо пропорциональными среднему напряжению.

Допущение 2 и вытекающие из него условия (2.39) и (2.40), как и в деформационной теории, означают инвариантность диаграммы «» относительно вида напряженного состояния.

Допущение 3 можно сформулировать в виде следующего соотношения:

   (2.41)

означающего, что девиатор приращения пластической деформации  пропорционален девиатору напряжений , причем коэффициент пропорциональности  есть некоторая функция напряжений.

  Из соотношения (2.41) следует, что

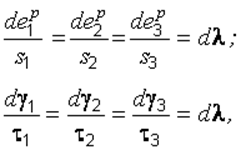   (2.42)

где  

  В свою очередь из соотношений (2.42) легко получить равенство

   (2.43)

означающее, что поле напряжений и поле приращений деформаций (скоростей деформаций) подобны.

2.6.7. Уравнения Сен-Венана–Мизеса

Подставляя соотношения (2.39) и (2.40) в равенство (2.38) и учитывая (2.42), получаем соотношения, устанавливающие связь между приращениями компонентов деформаций и напряжений:

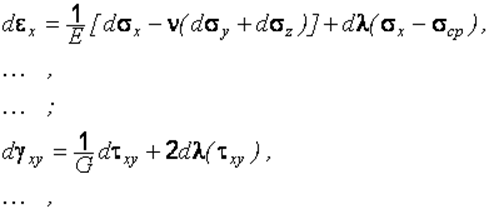    (2.44)

где .

Если деформации тел только упругие, то , если только пластичные, то .

Рассматривая последний случай и поделив обе части равенств (2.44) на dt,получим уравнения Сен-Венана–Леви–Мизеса

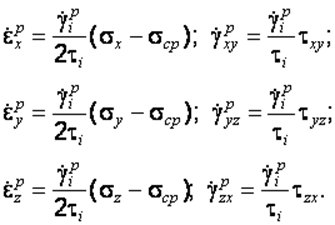   (2.45)

Хотя в уравнения (2.45) входят скорости деформаций, время в явном виде эти уравнения не учитывают, поскольку соотношения скоростей равносильны соотношениям приращений деформаций:

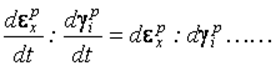  и т. д.

2.6.8. Пластический потенциал

Друкер и Прагер, обобщая теорию пластического течения, ввели понятие потенциала пластичности f, т. е. такой функции напряжения, частная производная от которой пропорциональна приращению пластической деформации:

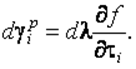   (2.46)

 Развернутый вид этого выражения следующий:

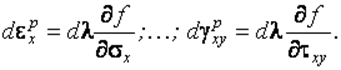   (2.47)

Если принять, что пластический потенциал совпадает с функцией нагружения (допущение Мизеса), то выражения (2.47) будут эквивалентны вторым членам правой части равенств (2.44), определяющим пластическую деформацию. Тогда выражения (2.47) можно записать в виде

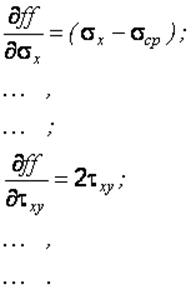   (2.48)

Отсюда следует, что частные производные от пластического потенциала равны компонентам девиатора напряжений.

Рассмотренные закономерности называют ассоциированным законом течения.

Пластический потенциал можно выразить также через интенсивность касательных напряжений. Для этого, используя выражение (2.15), следует определить значения , и тогда из сопоставления с соотношениями (2.48) получим

   (2.49)

2.6.9. Сопоставление теорий пластичности

При простом напряженном состоянии решения, получаемые по деформационной теории и по теории пластического течения, совпадают. Для сложного напряженного состояния тела теория пластического течения ближе соответствует опытным данным, деформационная же теория, строго говоря, несправедлива. Но когда отклонения от условий простого нагружения не очень велики, то разница в решениях по обеим теориям будет небольшая. Таким образом, теория пластического течения, оперирующая не самими деформациями, а их приращениями, более универсальна, тогда как деформационная теория более проста и поэтому получила широкое применение для решения инженерных задач.

Контрольные вопросы