Если процесс деформирования включает в себя как изменение
объема, так и изменение формы, и если он протекает во времени, то активная
деформация определяется условиями ![]() , а пассивная деформация
, а пассивная деформация ![]() . Случай
. Случай ![]() соответствует нейтральному деформированию.
соответствует нейтральному деформированию.
2.6.О теориях деформирования
2.6.1. Основные допущения теорий пластичности
2.6.2. Деформационная теория пластичности
2.6.3. Уравнения Генки
2.6.4. Упругие и пластические деформации
2.6.5. Разгрузка
2.6.6. Теория пластического течения
2.6.7. Уравнения Сен-Венана–Мизеса
2.6.8. Пластический потенциал
2.6.9. Сопоставление теорий пластичности
2.6.1. Основные допущения теорий пластичности
Теории деформирования определяют напряжения и деформации в точке тела при заданных ГУ. Для этого используют уравнения равновесия (2.19), уравнения совместности деформаций (2.22) и уравнения состояния (2.23).
Существует две основные группы теорий пластичности. Одна из них – деформационная теория – рассматривает связь между компонентами напряжений и деформаций; другая, называемая теорией пластического течения, рассматривает не сами деформации, а их приращения.
Обе теории пластичности время в явной форме не учитывают. Влияние временных эффектов рассматривается теорией ползучести.
Рассматриваемые теории пластичности исходят из следующих трех допущений:
1)
считается, что деформацию формы (или приращение этой деформации) вызывают
компоненты девиатора напряжений ![]() и она не
зависит от шарового тензора
и она не
зависит от шарового тензора ![]() ; деформация же
объема (или ее приращение) вызывается шаровым тензором напряжений
; деформация же
объема (или ее приращение) вызывается шаровым тензором напряжений ![]() и не
зависит от компонентов девиатора напряжений
и не
зависит от компонентов девиатора напряжений ![]() ;
;
2) связь между компонентами тензора напряжений и деформаций (или их приращений) остается неизменной при любом виде напряженного состояния;
3) напряженное и деформированное состояние тела принимаются подобными (см. условие 2.31).
2.6.2. Деформационная теория пластичности
Из группы деформационных теорий наибольшее распространение получила теория малых упругопластических деформаций, развитая А.А. Ильюшиным. Эта теория применима до относительных деформаций среды порядка 15–20 % [17]. Допущения 1 и 2 в этой теории формируются в виде зависимостей
![]() ;
(2.26)
;
(2.26)
![]() .
(2.27)
.
(2.27)
При большом развитии пластических деформаций упругими объемными деформациями можно пренебречь, и тогда условие (2.27) заменяется условием несжимаемости материала:
![]() .
(2.28)
.
(2.28)
Допущение 3 формулируется в виде соотношения
![]() ,
(2.29)
,
(2.29)
которое означает, что
девиатор деформаций пропорционален девиатору напряжений, причем коэффициент
пропорциональности ![]() называют
модулем пластичности.
называют
модулем пластичности.
Из соотношения (2.29) следует, что
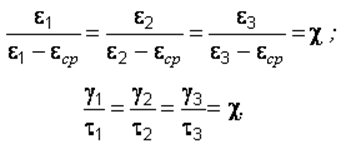 (2.30)
(2.30)
Соотношения (2.30) можно привести к виду
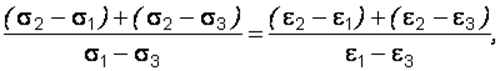
откуда
следует, что принятые допущения равносильны равенству параметров Надаи-Лоде для
напряжений ![]() и
деформаций
и
деформаций ![]() :
:
![]() (2.31)
(2.31)
т. е. условию подобия напряженного и деформированного состояния тела.
Значения параметров Надаи-Лоде равны соответственно
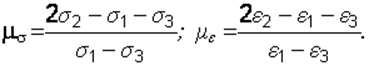 (2.32)
(2.32)
2.6.3. Уравнения Генки
Соотношения (2.25) для нелинейно-упругого и упругопластического тела принимают вид
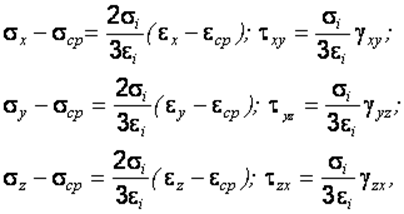 (2.33)
(2.33)
где ![]() –
интенсивности напряжений и деформаций (см. подразд. 2.2).
–
интенсивности напряжений и деформаций (см. подразд. 2.2).
Впервые эти соотношения при условии отсутствия упрочнения были получены Генки. Запись соотношений (2.33) выполнена в форме, установленной А.А. Ильюшиным. Для того, чтобы выражения (2.33) отражали физические свойства тела, необходимо из опытов определить вид функции для параметра пластичности. Эта функция будет равна
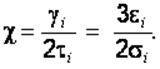 (2.34)
(2.34)
2.6.4. Упругие и пластические деформации
Если
деформации упруги, то ![]() , где G – модуль
сдвига.
Тогда, учитывая, что G = E/2(1+n)и
, где G – модуль
сдвига.
Тогда, учитывая, что G = E/2(1+n)и ![]() , где K = E/(1–2n) уравнения
Генки приводят к известному в теории упругости обобщенному закону Гука:
, где K = E/(1–2n) уравнения
Генки приводят к известному в теории упругости обобщенному закону Гука:
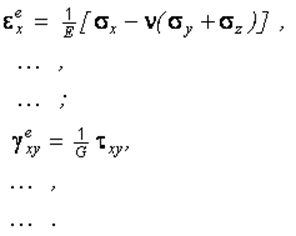 (2.35)
(2.35)
Если деформации включают в себя упругую и пластическую составляющие, то
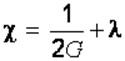 ,
(2.36)
,
(2.36)
где ![]() –
некоторая функция, характеризующая пластическую часть деформаций. Тогда
соотношение (2.36) можно записать в виде
–
некоторая функция, характеризующая пластическую часть деформаций. Тогда
соотношение (2.36) можно записать в виде
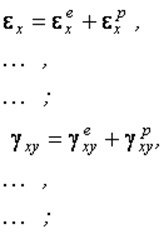 (2.37)
(2.37)
где
индексы eи
pозначают
упругую и пластическую части деформаций, причем ![]() и
и
![]() определяются
выражениями (2.35), а
определяются
выражениями (2.35), а ![]() и
и
![]() следующими
выражениями:
следующими
выражениями:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.