Исследование напряженно-деформированного состояния однородной цилиндрической оболочки при действии бокового давления, страница 2

Подставляя принятые ранее гипотезы в уравнения геометрии(4-5):

Получаем первые 2 уравнения геометрии:

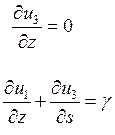
                                                                                                  (9)

- функция не зависящая от z

 - находится путём интегрирования второго выражения в пределах [0;z].

Это позволяет выразить компоненты вектора перемещения каждого слоя через перемещения срединных поверхностей.

 

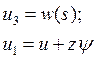Где  - прогиб срединной поверхности слоя, - перемещение срединной поверхности вдоль образующей; -

угол поворота нормали к срединной поверхности: .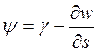

Учитывая эти уравнения получаем остальные 3 уравнения геометрии.

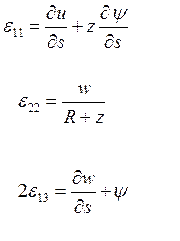
                                                                                 (10)

Подставив равенства  из уравнений геометрии (10) в уравнения закона Гука, определяем компоненты тензора напряжений.

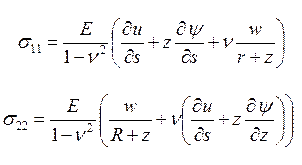
(11)

Вводим в рассмотрение удельные силовые факторы с целью понижения размерности.

 

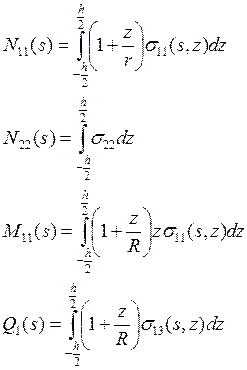                                                                                                               (12)

Где: (s)- отнесённая к единице длинны в окружном направлении удельная тангенсальная сила, действующая в напряжении образующей.

- отнесённая к единице длинны в направлении образующей удельная тангенсальная сила, действующая в этом направлении.

- отнесённая к единице длинны в окружном направлении изгибающий момент, действующий в направлении образующей.

- отнесённая к единице длинны в окружном направлении удельная поперечная сила.

Для перехода к удельным силовым факторам мы проинтегрировали по толщине уравнения равновесия(2).

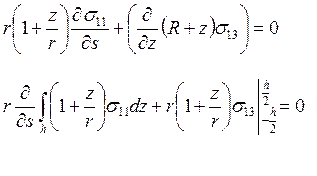
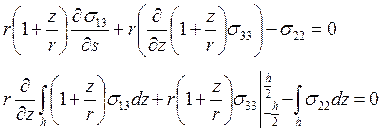
                                                                                                               (13)

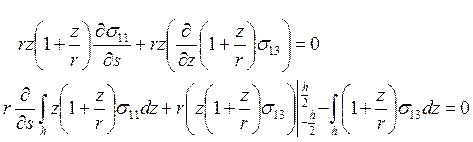
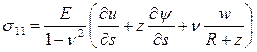Аналогично мы поступили с законами Гука, проинтегрировав компоненты тензора напряжений (11).

 

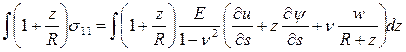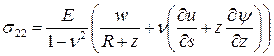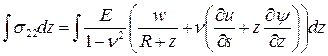                                                                                                               (14)

 

                                                                

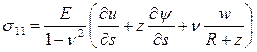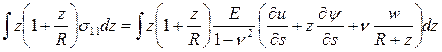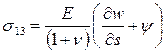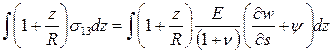
В итоге мы получили фундаментальные уравнения нашей задачи.

 

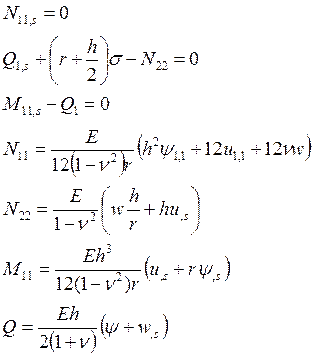                                                                                                               (15)

Численное решение

Для численного решения мы использовали пакет Maple, где применили метод Бубнова- Галёркина. Мы представили искомые функции в виде линейной комбинации ортогональных полиномов Лежандра:

 

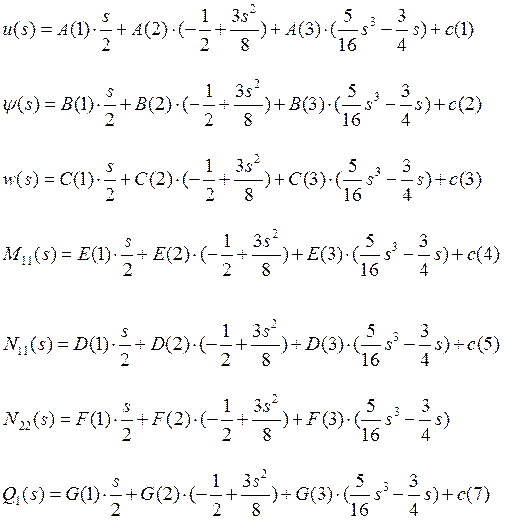                                                                                                               (16)

Коэффициенты при полиномах находим методом минимизации невязок:

Е[i]- i-е фундаментальное уравнение в которые подставлены искомые функции в виде разложения.

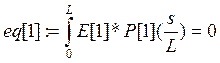
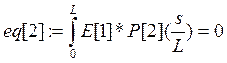
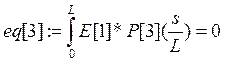
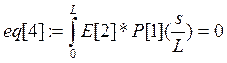
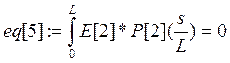
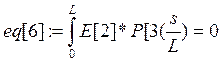
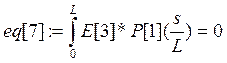
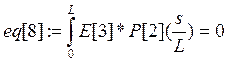
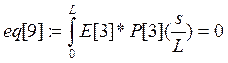
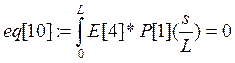
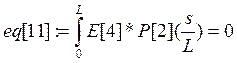
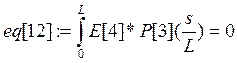
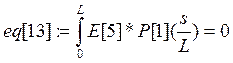
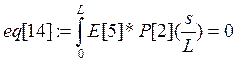
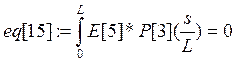
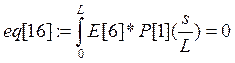
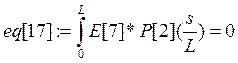
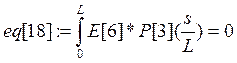
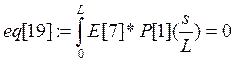
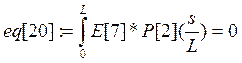
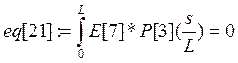
а константы интегрирования из граничных условий:

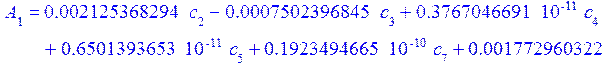
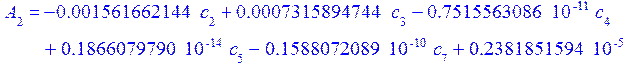
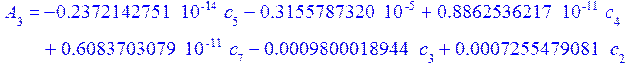
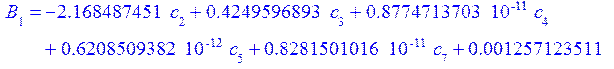
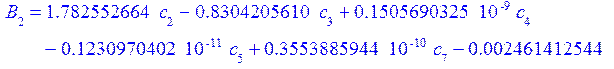
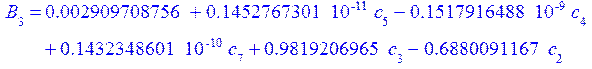
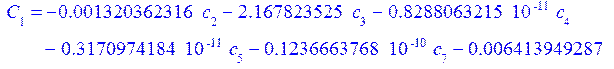
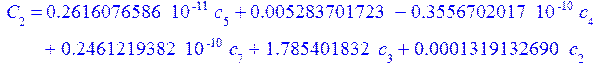
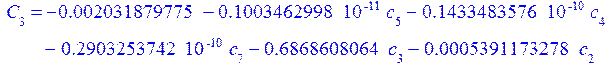
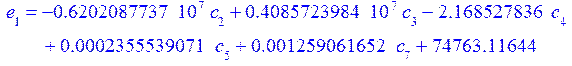
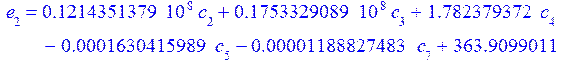
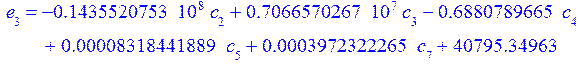
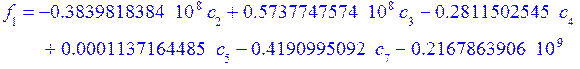
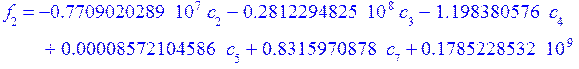
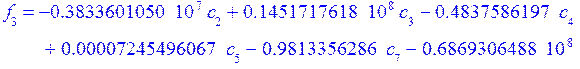
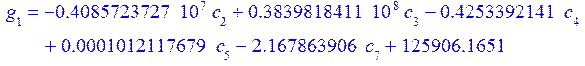
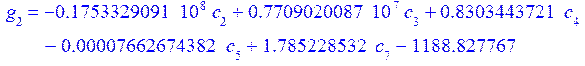
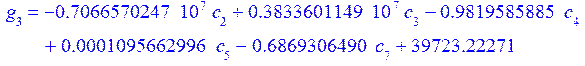
В итоге получили графики перемещений, прогиба срединной поверхности и непряжения.

Как видно на графике (рис.2-3) перемещение верхней и нижней лицевой поверхности  разных знаков. Где максимальное перемещение у верхней лицевой поверхности, там минимальное у нижней, и наоборот.