Из графика прогиба срединной поверхности (рис.1) можно сказать, что максимальный прогиб будет отрицателен. А максимальное угловое напряжение (рис.4) отрицательно и меняет свой знак.
Модель задачи в Ansys.
Сравнение результатов.
Также задача была смоделирована в конечно разностном пакете Ansys. Результаты мы сравнили с результатами полученными в программе Maple.
Перемещение верхней лицевой поверхности в Ansys (рис.7) и в программе Maple (рас.2), практически полностью совпадают численно и знаками. В нижней части цилиндра перемещение будет максимальное, а в верхней минимальное.
Аналогично можно сказать, что перемещение нижней лицевой поверхности в Ansys (рис.6) совпадает с перемещением в Maple (рис.3). Только теперь в нижней части цилиндра перемещение будет минимальное, а в верхней максимальное.
Модели прогиба срединной поверхности (рис.7) также аналогична результатам полученным в программе Maple (рис.1). Здесь хорошо видно закрепление на концах и отрицательный прогиб. И напряжение в программе Ansys (рис.8), совпадает с результатами полученными в Maple (рис.4).
Вывод.
В работе был попробован метод коечных элементов, но он
не дал результатов, так как матрица имеет плохую обусловленность. Поэтому был
применён метод Бубнова- Галёркина. Были определены перемещения которые имеют
максимальные значения: max=0,00015, min=-0,00015 на верхней лицевой
поверхности, max=0,0004, min=-0,0004 на нижней лицевой
поверхности, прогиб имеет максимальное значение -0,003, а угловое напряжение- ![]() . Также полученные результаты
сравнили с результатами полученными в программе Ansys. Полученные результаты практически совпадают, что
свидетельствует о возможности применения выбранного метода для решения задач
механики деформируемого твёрдого тела.
. Также полученные результаты
сравнили с результатами полученными в программе Ansys. Полученные результаты практически совпадают, что
свидетельствует о возможности применения выбранного метода для решения задач
механики деформируемого твёрдого тела.
Приложение.
Maple.
> restart: with(orthopoly): R:=0.45;h:=0.1;L:=2;nu:=0.3;E:=1.60*10^11;sigma:=-200*10^6;
>
![]()
![]()
![]()
![]()
![]()
![]()
>
> de[1]:=diff(N11(s),s);
![]()
> de[2]:=diff(Q1(s),s)+(R+h/2)*sigma-N22(s);
![]()
> de[3]:=diff(M11(s),s)-Q1(s);
![]()
> de[4]:=E/(12(1-nu^2)*R)*(h^2*diff(psi(s),s)+12*diff(u(s),s)+12*nu*w(s))-N11(s);
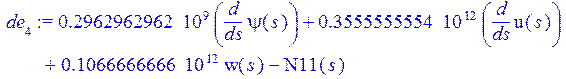
> de[5]:=E*h^3/(12*(1-nu^2)*R)*(diff(u(s),s)+R*diff(psi(s),s))-M11(s);
![]()
> de[6]:=E/(1-nu^2)*(w(s)*(h/R)+h*diff(u(s),s))-N22(s);
![]()
> W:=rhs(isolate(de[6]=0,w(s)));
![]()
> de[7]:=E*h/(2*(1+nu))*(psi(s)+diff(w(s),s))-Q1(s);
![]()
> N11(s):=sum(P(i,s/L)*d[i],i=1..3)+c[5];
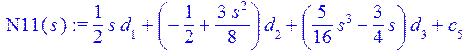
> u(s):=sum(P(i,s/L)*A[i],i=1..3)+c[1];
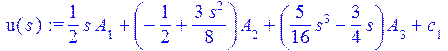
> psi(s):=sum(P(i,s/L)*B[i],i=1..3)+c[2];
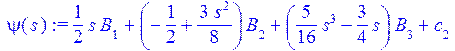
> w(s):=sum(P(i,s/L)*C[i],i=1..3)+c[3];
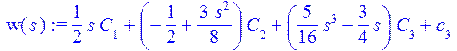
> M11(s):=sum(P(i,s/L)*e[i],i=1..3)+c[4];
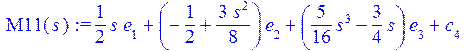
> N22(s):=sum(P(i,s/L)*f[i],i=1..3);
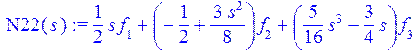
> Q1(s):=sum(P(i,s/L)*g[i],i=1..3)+c[7];
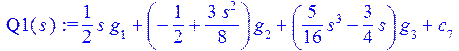
> de[1]:=eval(de[1]);
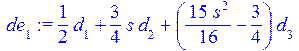
> eq[1]:=int(de[1]*P(1,s/L),s=0..L)=0;
![]()
> eq[2]:=int(de[1]*P(2,s/L),s=0..L)=0;
![]()
> eq[3]:=int(de[1]*P(3,s/L),s=0..L)=0;
![]()
>
> de[2]:=eval(de[2]);
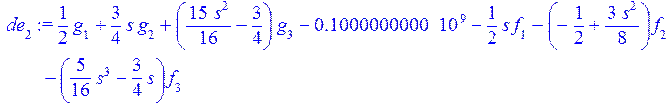
>
> eq[4]:=int(de[2]*P(1,s/L),s=0..L)=0;
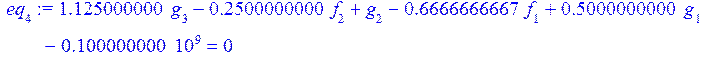
> eq[5]:=int(de[2]*P(2,s/L),s=0..L)=0;
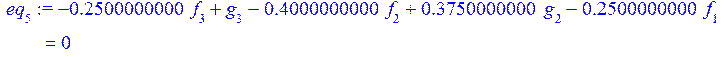
> eq[6]:=int(de[2]*P(3,s/L),s=0..L)=0;
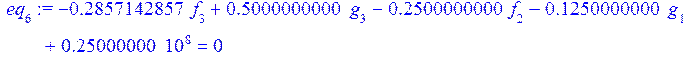
>
> de[3]:=eval(de[3]);
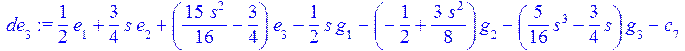
> eq[7]:=int(de[3]*P(1,s/L),s=0..L)=0;
![]()
> eq[8]:=int(de[3]*P(2,s/L),s=0..L)=0;
![]()
> eq[9]:=int(de[3]*P(3,s/L),s=0..L)=0;
![]()
> ![]()
> de[4]:=eval(de[4]);
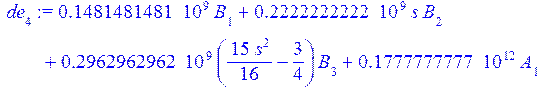
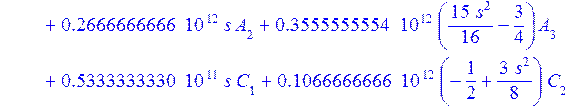
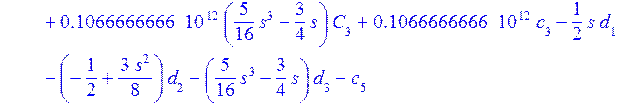
> eq[10]:=int(de[4]*P(1,s/L),s=0..L)=0;
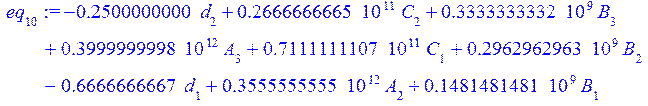
![]()
> eq[11]:=int(de[4]*P(2,s/L),s=0..L)=0;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.