находится путём интегрирования второго выражения в пределах [0;z]. Это позволяет выразить компоненты вектора перемещения каждого слоя через перемещения срединных поверхностей.
 |
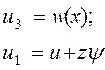Где 
-
прогиб срединной поверхности слоя, 
-
перемещение срединной поверхности вдоль образующей; 
-
угол поворота
нормали к срединной поверхности: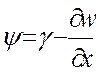 
.
Учитывая эти уравнения, получаем остальные 3 уравнения геометрии.
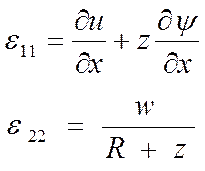
(10)
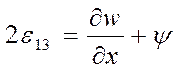
Подставив
равенства 
из
уравнений геометрии (10) в уравнения закона Гука, определяем компоненты тензора
напряжений.
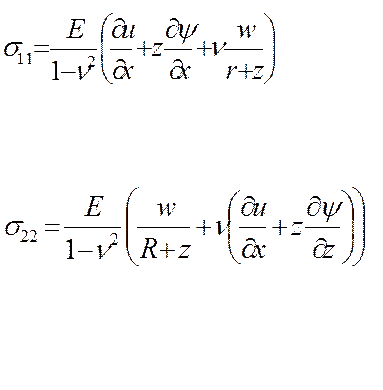
(11)
Вводим в рассмотрение удельные силовые факторы с целью понижения размерности.
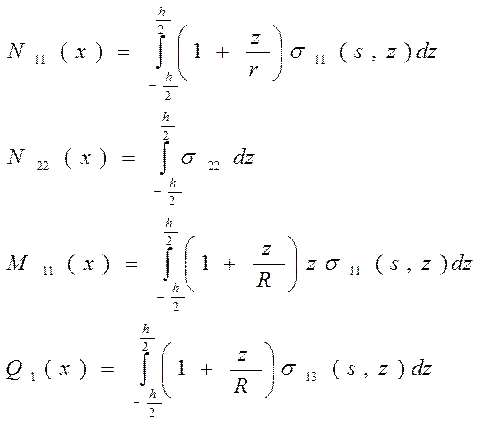
(12)
Где:
(x)-
отнесённая к единице длины в окружном направлении удельная тангенсальная сила,
действующая в напряжении образующей.
-
отнесённая к единице длины в направлении образующей удельная тангенсальная
сила, действующая в этом направлении.
-
отнесённый к единице длины в окружном направлении изгибающий момент,
действующий в направлении образующей.
-
отнесённая к единице длины в окружном направлении удельная поперечная сила.
Для перехода к удельным силовым факторам мы проинтегрировали по толщине уравнения равновесия(2).
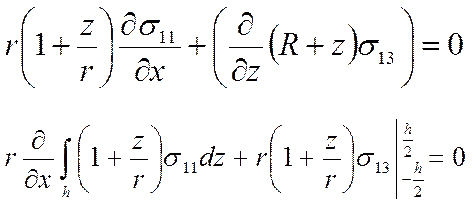
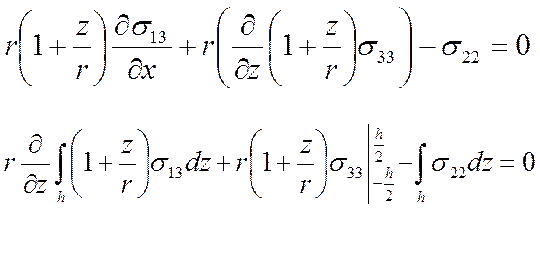
(13)
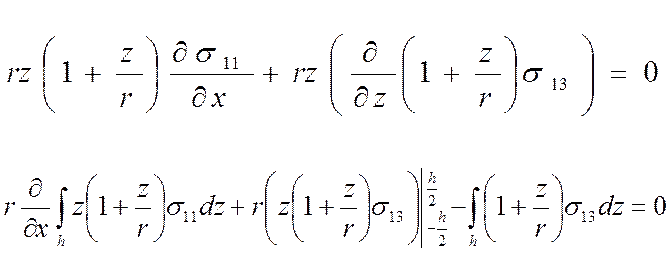
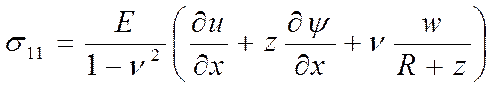Аналогично
мы поступили с законами Гука, проинтегрировав компоненты тензора напряжений
(11).
 |
||||
 |
||||
 |
||||
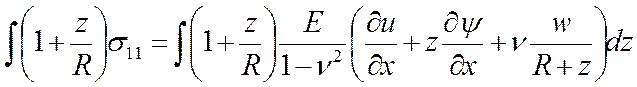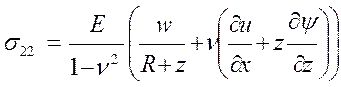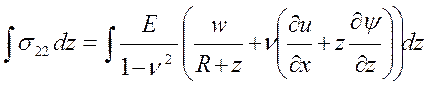(14)
 |
|||
 |
|||
 |
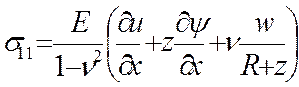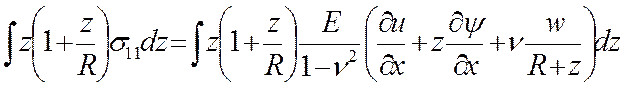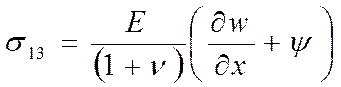
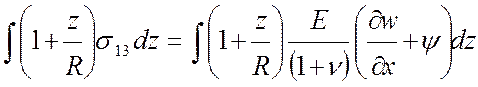В итоге мы получили фундаментальные уравнения математической модели для нашей задачи.
 |
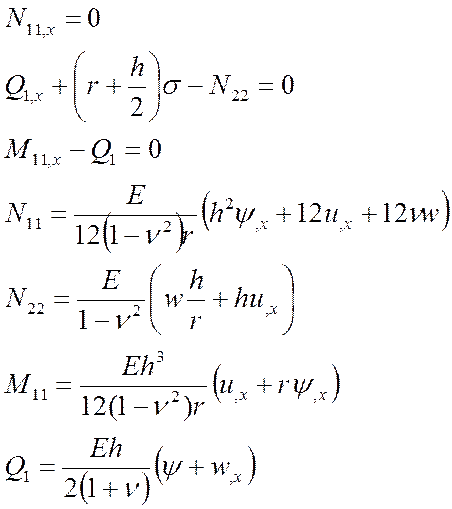(15)
Система уравнений (15) может быть сведена к трём уравнениям:
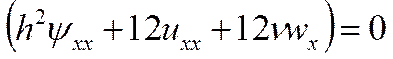
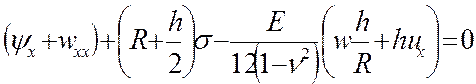(16)
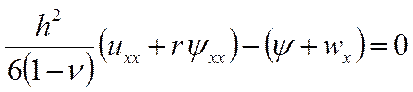
С помощью пакета MAPLE находим следующее решение:
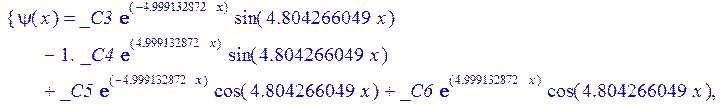
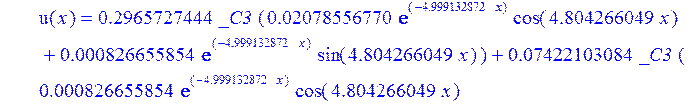
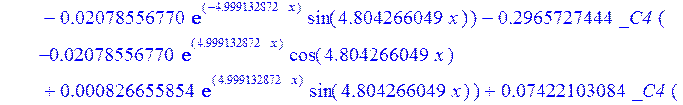
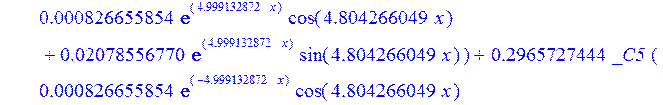
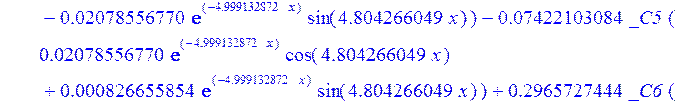
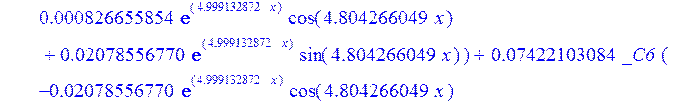
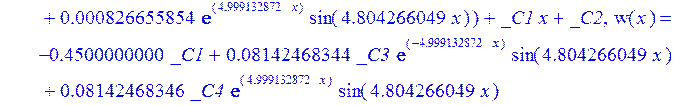
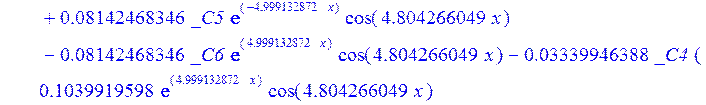
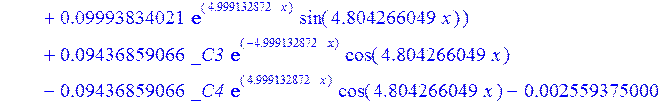
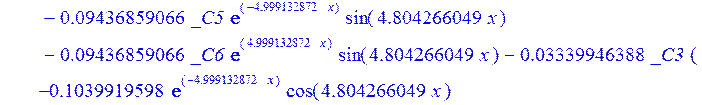
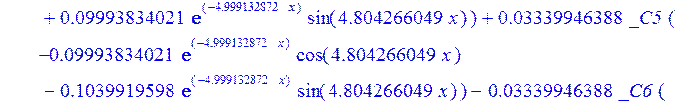
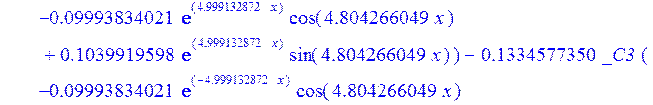
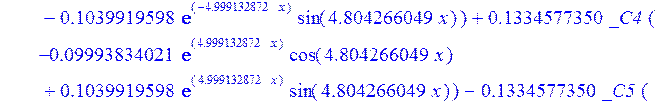
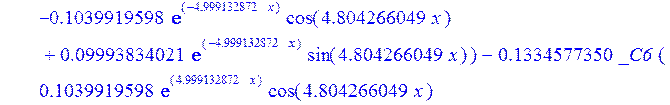
Константы интегрирования определяются из граничных условий:
;
;
;
;
;
;
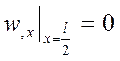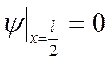C1=0.0001470394498
C2=-0.00014770394499
C3=0.02361674909
C4=0.1055979298*10-5
C5=-0.1962543581*10-6
C6=0.1962453581*10-6
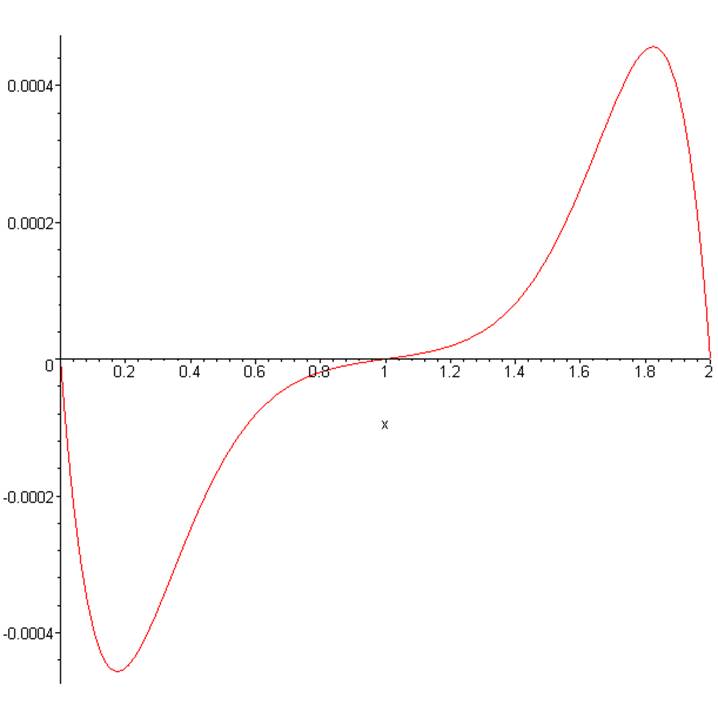
Рис.1. Перемещение нижней лицевой поверхности по образующей.
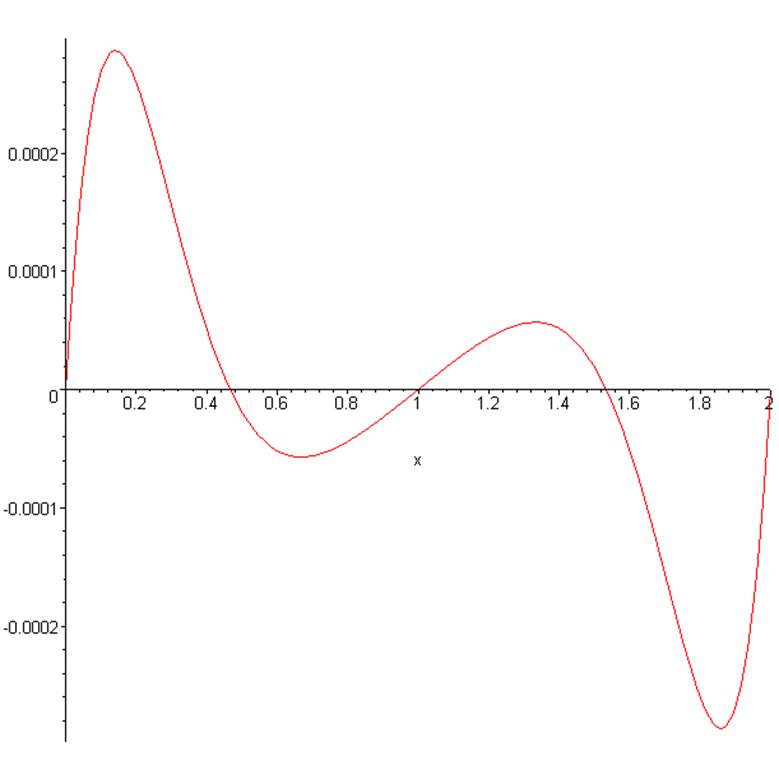
Рис.2. Перемещение верхней лицевой поверхности по образующей.
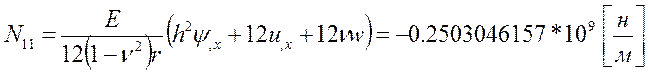
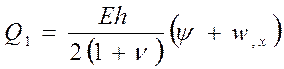
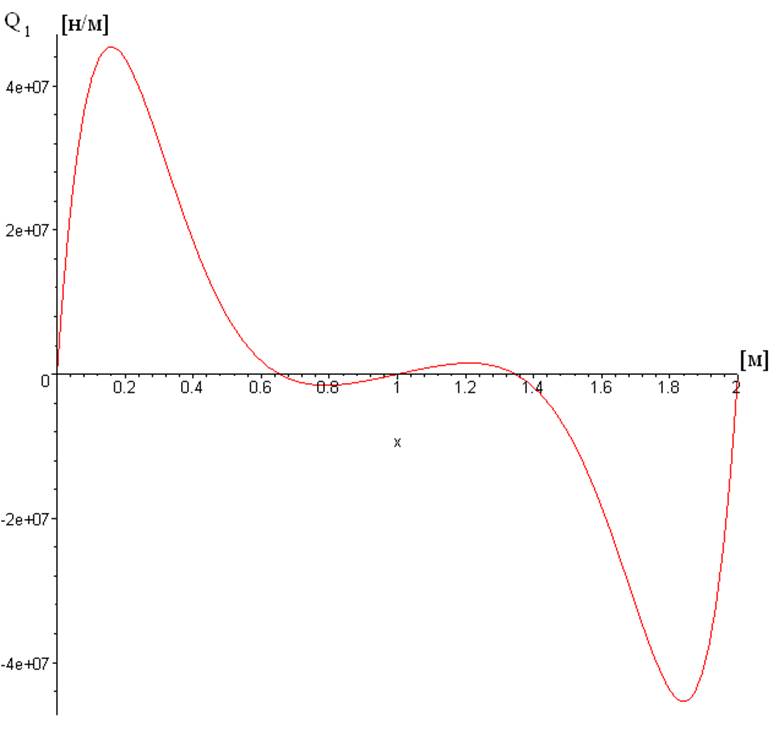
Рис .3.
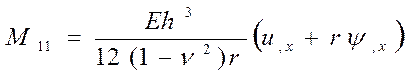
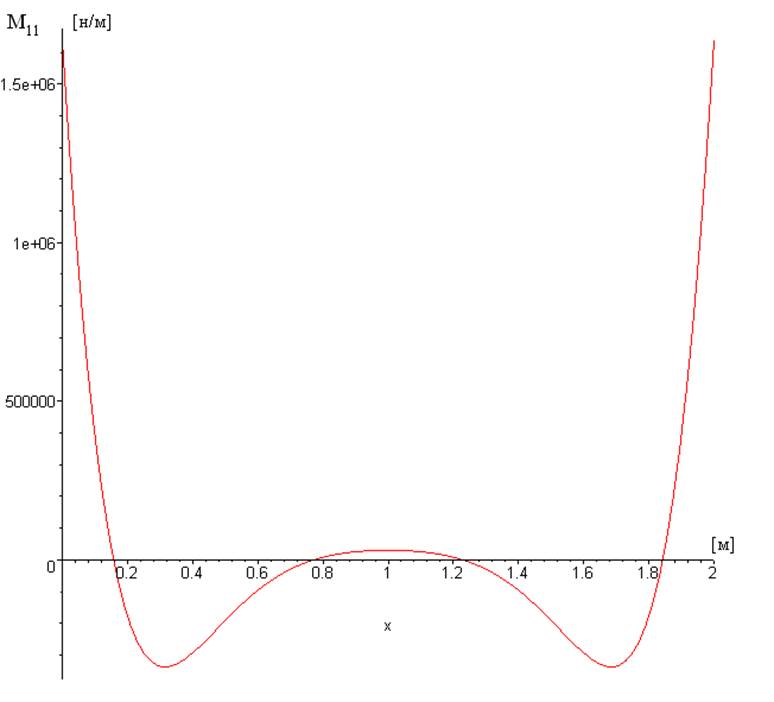
Рис. 4.
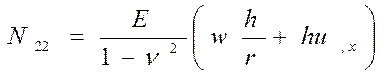
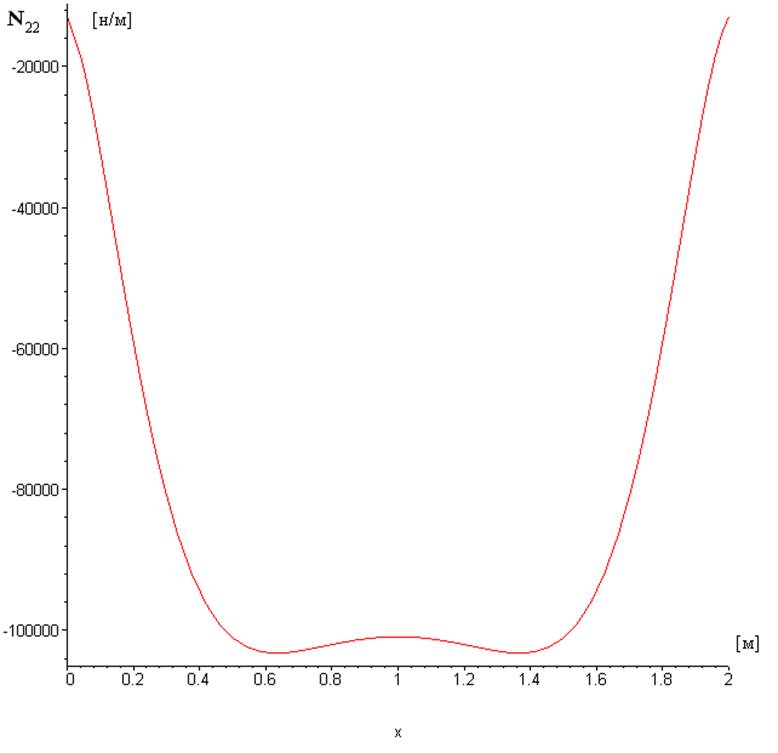
Рис. 5.
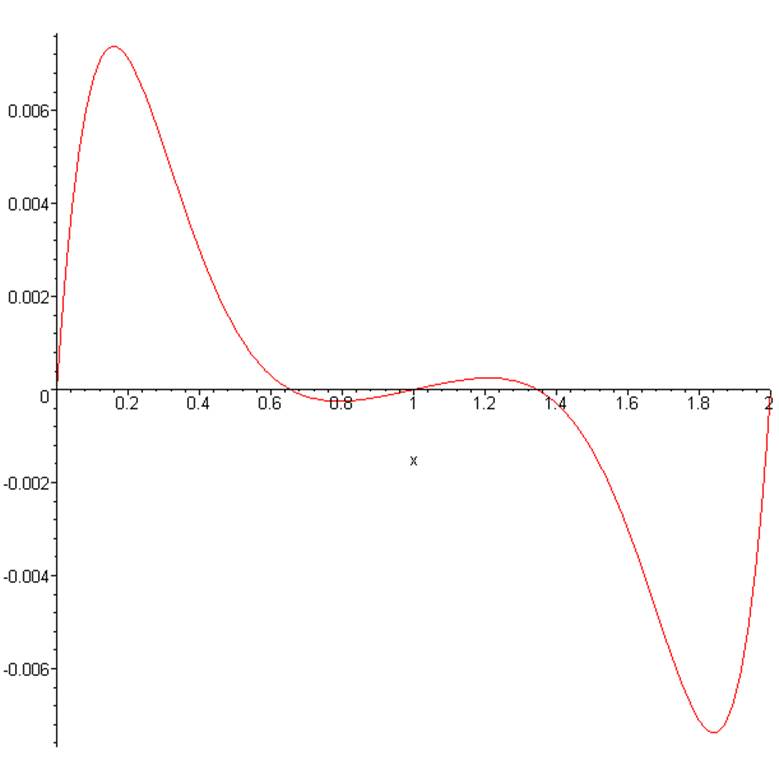
Рис. 6. Угол поворота нормали к срединной поверхности.
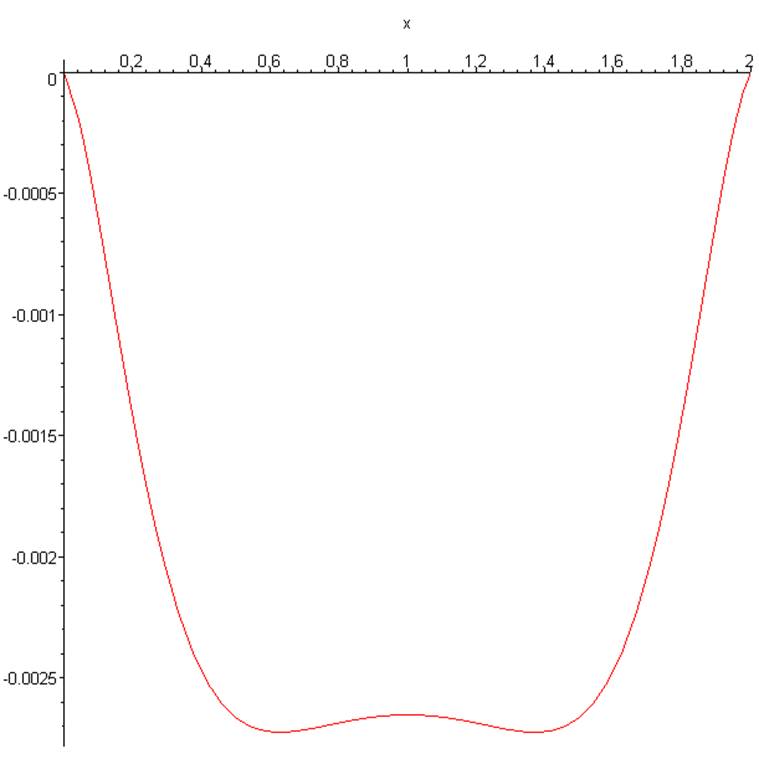
Рис. 7. Прогиб срединной поверхности слоя
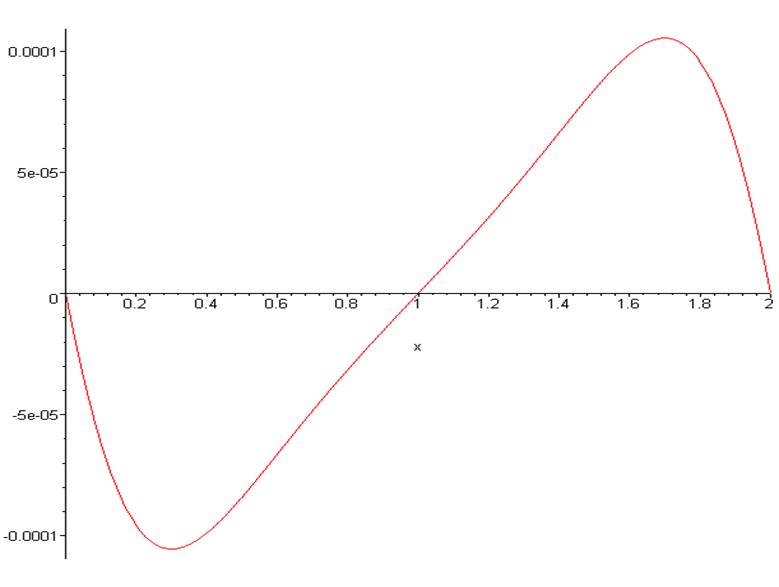
Рис. 8. Перемещение срединной поверхности вдоль образующей.
Результаты расчёта из работы [ 9].
 |
Рис. 10. Прогиб срединной поверхности.
 |
Рис. 11. Перемещение верхней лицевой поверхности по образующей.
Рис.12. Перемещение нижней лицевой поверхности по образующей.
ЗАКЛЮЧЕНИЕ
Основные результаты выпускной квалификационной работы могут быть сформулированы следующим образом:
1. Проведён литературный обзор по способам изготовления цилиндрических оболочек и их практическом применении.
2. На базе безмоментной теории тонких оболочек построена физически состоятельная модель осесимметричного деформирования однородной цилиндрической оболочки.
3. С помощью математического пакета Maple найдено аналитическое решение, удовлетворяющее поставленным граничным условиям жёсткого закрепления на торцах. Определены функции перемещений и удельных силовых факторов.
4. Найденное решение сопоставлено с решением такой же задачи, найденным методом минимизации невязок и с помощью конечно-элементного пакета Ansys. Качественное и количественное сопоставление результатов позволяет сделать вывод о достоверности полученного решения.
5. В дальнейшем планируется подготовка магистерской диссертации, в которой будет приведено решение данной задачи методом сеток без применения гипотез, понижающих размерность задачи. Предполагается построение конечно-разностной схемы и отработка методов её решения, т.к. она может иметь плохую обусловленность.
Список литературы:
1. Пикуль, В.В. Современные проблемы науки в области прикладной механики: учебник. В 2 ч. Ч. 2. Механика оболочек/ В.В. Пикуль.- Владивосток: изд-во ДВГТУ, 2005.-524 с.
2. Власов В.З. Общая теория оболочек//Избранные труды, Т.1. М: Из-во АН СССР, 1962.- 528 с.
3. Гольденвейзер А.Л. Теория тонких упругих оболочек. М.:Наука, 1976.-512 с.
4. Григоренко Я.М., Мукоед А.П. Решение задач теории оболочек на ЭВМ: Учеб. Пособие. Киев: Виша шк., 1979.-280 с.
5. Новожилов В.В. Теория тонких оболочек. Л.:Судпромгиз, 1962.-432 с.
6. Пикуль, В.В. Современные проблемы науки в области прикладной механики: учебник. В 2 ч. Ч. 1. Механика деформированного твёрдого тела/ В.В. Пикуль.- Владивосток: изд-во ДВГТУ, 2003.-423 с.
7. Борис П.Д. Основы вычислительной математики М., 1966 г. 664 стр. с илл.
8. Вычислительная математика: учеб.- метод. комплекс / А.А. Бочарова; Е.П. Луппова; А.А. Ратников/ под ред. А.А. Бочаровой; ДВГТУ.- Владивосток: Изд-во ДВГТУ, 2008.- 175 с.
9. Апарина Н.А. Бакалаврская работа на тему «Исследование напряженно-деформированного состояния однородной цилиндрической оболочки при действии бокового давления»/ под рук. А.А. Ратникова, ДВФУ, 2011
Приложение.
> restart;
> h:=0.1; nu:=0.3; E:=1.6e11; P:=2e8; R:=0.45;
> de[1]:=eval(h^2*diff(psi(x),x$2)+12*diff(u(x),x$2)+12*nu*diff(w(x),x))=0;
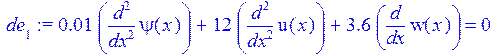
> de[2]:=h^2/(6*(1-nu)*R)*(diff(u(x),x$2)+R*diff(psi(x),x$2))-(psi(x)+diff(w(x),x))=0;
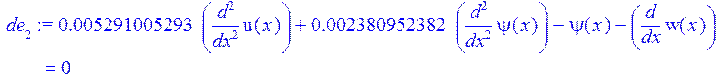
> de[3]:=1/(2*(1+nu))*(diff(psi(x),x)+diff(w(x),x$2))-(R/h+1/2)*P/E-1/(1-nu^2)*(w(x)/R+diff(u(x),x))=0;
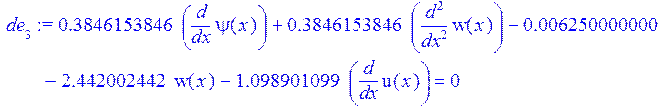
> evalf({psi(x) = _C3*exp(-1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*sin(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)-_C4*exp(1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*sin(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)+_C5*exp(-1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*cos(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)+_C6*exp(1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*cos(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x), u(x) = int(int(48872540827875548503655735949834430/164791073190440605071076708156964757*_C3*exp(-1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*sin(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)+232142857190/462275615730949412908469256326011388156692260244839*_C3*cos(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*21844659747877709269489224499309191693907059975062190504275542156852466793839^(1/2)*exp(-1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)-48872540827875548503655735949834430/164791073190440605071076708156964757*_C4*exp(1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*sin(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)+232142857190/462275615730949412908469256326011388156692260244839*cos(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*_C4*21844659747877709269489224499309191693907059975062190504275542156852466793839^(1/2)*exp(1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)+48872540827875548503655735949834430/164791073190440605071076708156964757*_C5*exp(-1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*cos(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)-232142857190/462275615730949412908469256326011388156692260244839*_C5*sin(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*21844659747877709269489224499309191693907059975062190504275542156852466793839^(1/2)*exp(-1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)+48872540827875548503655735949834430/164791073190440605071076708156964757*_C6*exp(1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*cos(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)+232142857190/462275615730949412908469256326011388156692260244839*_C6*sin(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*21844659747877709269489224499309191693907059975062190504275542156852466793839^(1/2)*exp(1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x),x),x)+_C1*x+_C2, w(x) = -3125000/1221001221-1098901099/2442002442*_C1-516761310666333055535/1430827388980823781829428995159570687651330112*_C3*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*exp(-1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*sin(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)+516761310666333055535/1430827388980823781829428995159570687651330112*_C3*exp(-1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*cos(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)-516761310666333055535/1430827388980823781829428995159570687651330112*_C4*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*exp(1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*sin(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)-516761310666333055535/1430827388980823781829428995159570687651330112*_C4*exp(1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*cos(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)-516761310666333055535/1430827388980823781829428995159570687651330112*_C5*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*exp(-1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*cos(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)-516761310666333055535/1430827388980823781829428995159570687651330112*_C5*exp(-1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*sin(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)+516761310666333055535/1430827388980823781829428995159570687651330112*_C6*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*exp(1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*cos(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)-516761310666333055535/1430827388980823781829428995159570687651330112*_C6*exp(1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*sin(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)-1/130785504505704881559872578521204861556655901200345823574614628387200*_C3*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(3/2)*exp(-1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*sin(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)-1/130785504505704881559872578521204861556655901200345823574614628387200*_C3*exp(-1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*cos(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(3/2)-1/130785504505704881559872578521204861556655901200345823574614628387200*_C4*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(3/2)*exp(1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*sin(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)+1/130785504505704881559872578521204861556655901200345823574614628387200*_C4*exp(1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*cos(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(3/2)-1/130785504505704881559872578521204861556655901200345823574614628387200*_C5*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(3/2)*exp(-1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*cos(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)+1/130785504505704881559872578521204861556655901200345823574614628387200*_C5*exp(-1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*sin(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(3/2)+1/130785504505704881559872578521204861556655901200345823574614628387200*_C6*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(3/2)*exp(1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*cos(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)+1/130785504505704881559872578521204861556655901200345823574614628387200*_C6*exp(1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*sin(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(3/2)-1098901099/2442002442*int(48872540827875548503655735949834430/164791073190440605071076708156964757*_C3*exp(-1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*sin(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)+232142857190/462275615730949412908469256326011388156692260244839*_C3*cos(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*21844659747877709269489224499309191693907059975062190504275542156852466793839^(1/2)*exp(-1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)-48872540827875548503655735949834430/164791073190440605071076708156964757*_C4*exp(1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*sin(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)+232142857190/462275615730949412908469256326011388156692260244839*cos(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*_C4*21844659747877709269489224499309191693907059975062190504275542156852466793839^(1/2)*exp(1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)+48872540827875548503655735949834430/164791073190440605071076708156964757*_C5*exp(-1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*cos(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)-232142857190/462275615730949412908469256326011388156692260244839*_C5*sin(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*21844659747877709269489224499309191693907059975062190504275542156852466793839^(1/2)*exp(-1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)+48872540827875548503655735949834430/164791073190440605071076708156964757*_C6*exp(1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*cos(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)+232142857190/462275615730949412908469256326011388156692260244839*_C6*sin(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*21844659747877709269489224499309191693907059975062190504275542156852466793839^(1/2)*exp(1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x),x)+12500/32078810840933253735793030480944913516208889811869337*_C3*cos(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*(-4568234214707010415485787405643253539931053374695435133124657686603129358558660822659626180215+13988958026497421573933356258658622945211964697175925076270000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*exp(-1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)+12500/32078810840933253735793030480944913516208889811869337*_C3*sin(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*(4568234214707010415485787405643253539931053374695435133124657686603129358558660822659626180215+13988958026497421573933356258658622945211964697175925076270000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*exp(-1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)-12500/32078810840933253735793030480944913516208889811869337*cos(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*_C4*(-4568234214707010415485787405643253539931053374695435133124657686603129358558660822659626180215+13988958026497421573933356258658622945211964697175925076270000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*exp(1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)+12500/32078810840933253735793030480944913516208889811869337*_C4*sin(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*(4568234214707010415485787405643253539931053374695435133124657686603129358558660822659626180215+13988958026497421573933356258658622945211964697175925076270000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*exp(1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)-12500/32078810840933253735793030480944913516208889811869337*_C5*sin(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*(-4568234214707010415485787405643253539931053374695435133124657686603129358558660822659626180215+13988958026497421573933356258658622945211964697175925076270000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*exp(-1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)+12500/32078810840933253735793030480944913516208889811869337*_C5*cos(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*(4568234214707010415485787405643253539931053374695435133124657686603129358558660822659626180215+13988958026497421573933356258658622945211964697175925076270000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*exp(-1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)-12500/32078810840933253735793030480944913516208889811869337*_C6*sin(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*(-4568234214707010415485787405643253539931053374695435133124657686603129358558660822659626180215+13988958026497421573933356258658622945211964697175925076270000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*exp(1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)-12500/32078810840933253735793030480944913516208889811869337*_C6*cos(1/3656220324349905033174*(-12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)*(4568234214707010415485787405643253539931053374695435133124657686603129358558660822659626180215+13988958026497421573933356258658622945211964697175925076270000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*exp(1/3656220324349905033174*(12768777069609408097260548966146789632819870+39100860000000*67528430782710119916462692888880815255990210117187437256508962^(1/2))^(1/2)*x)});
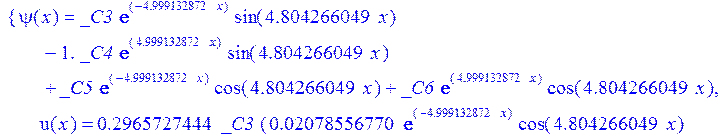
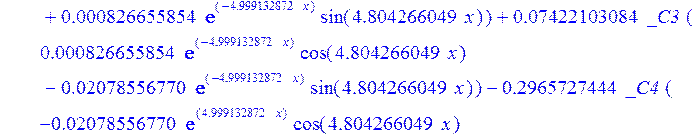
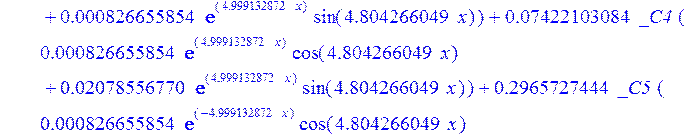
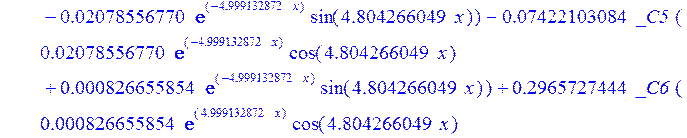
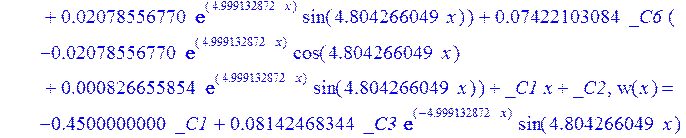
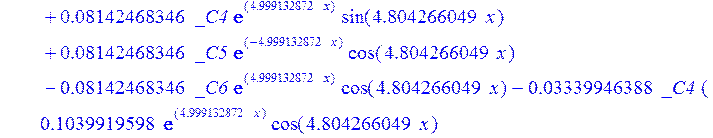
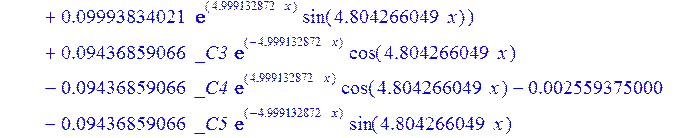
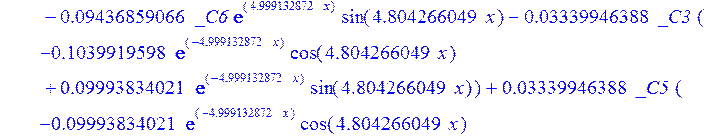
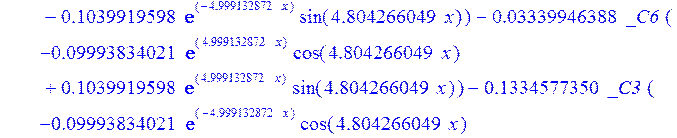
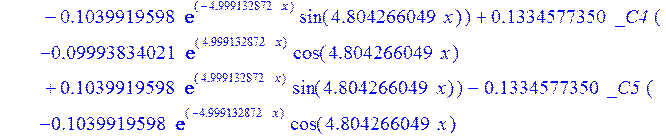
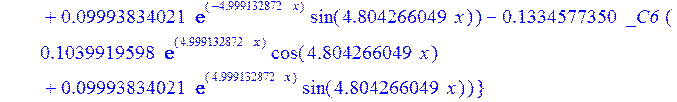
> dsolve({de[1],de[2],de[3]},{u(x),psi(x),w(x)});
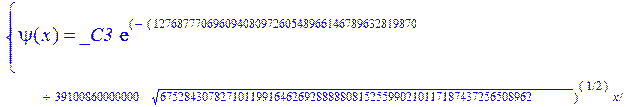
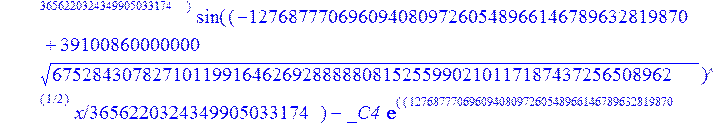
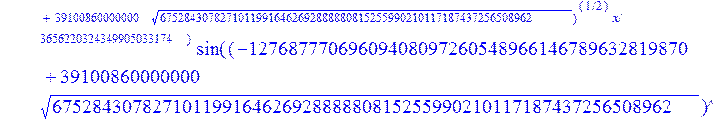
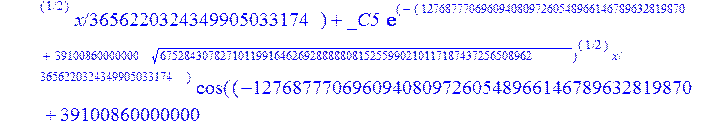
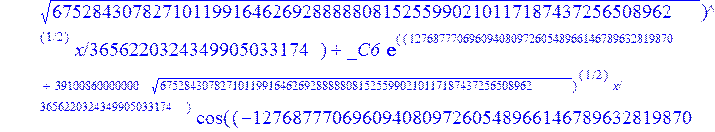
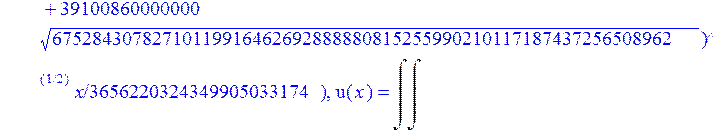
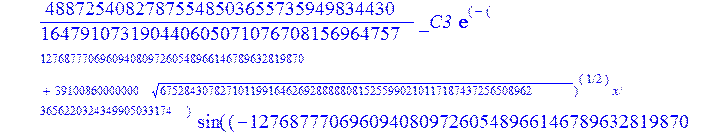
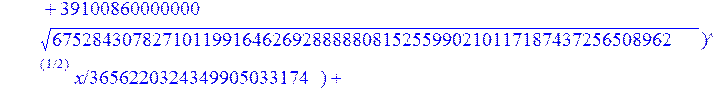
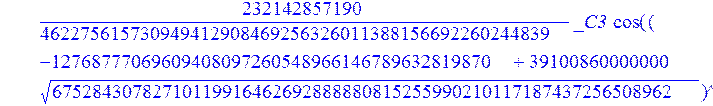
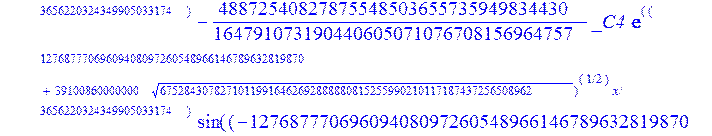
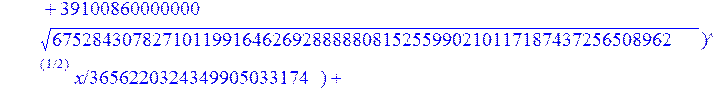
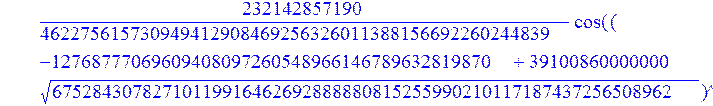
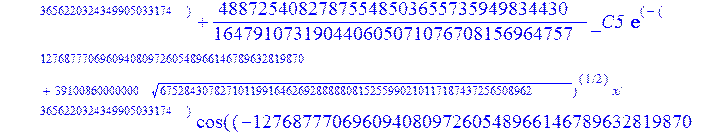
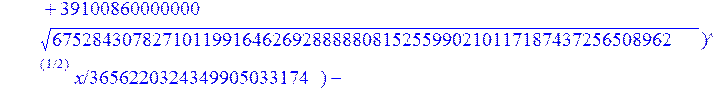
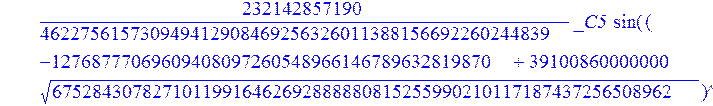
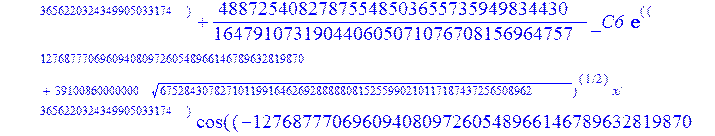
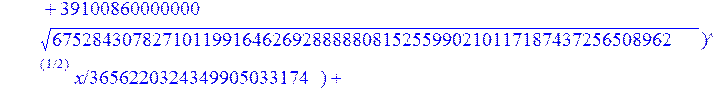
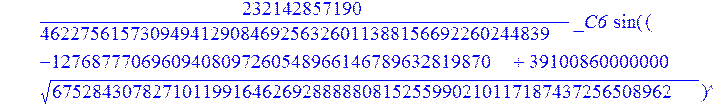
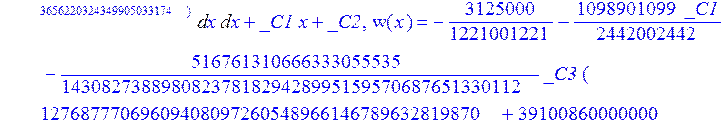
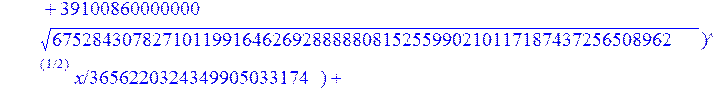
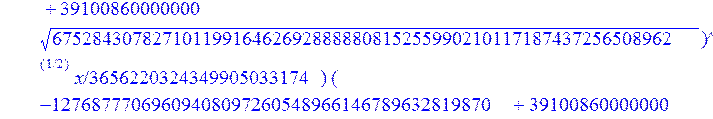
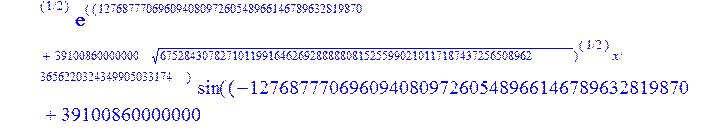
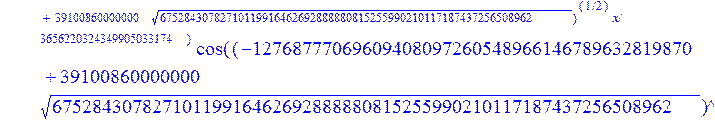
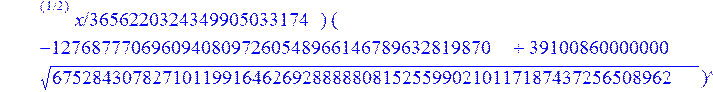
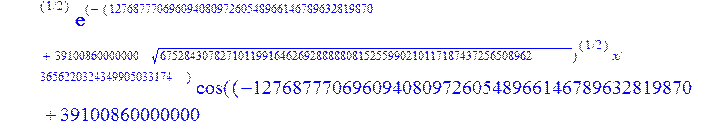
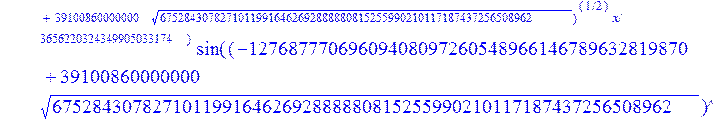
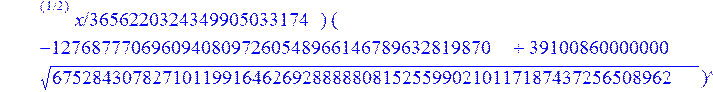
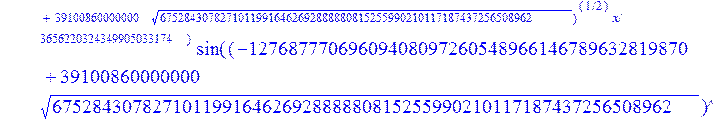
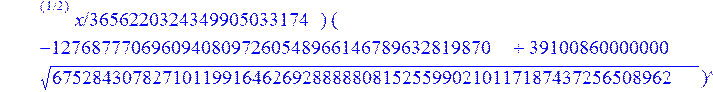
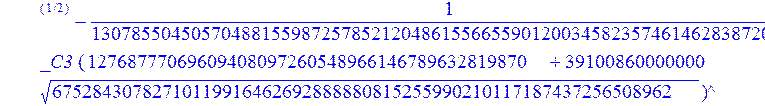
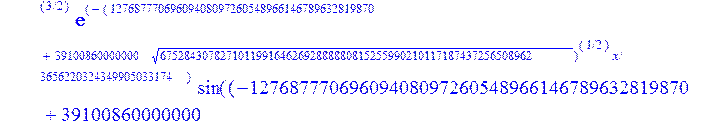
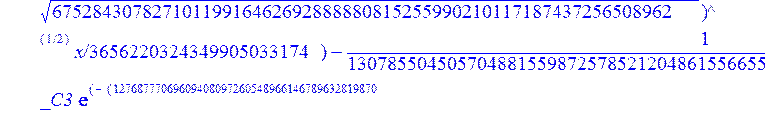
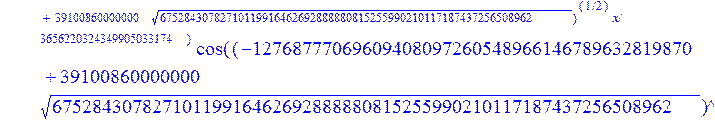
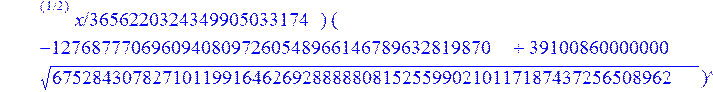
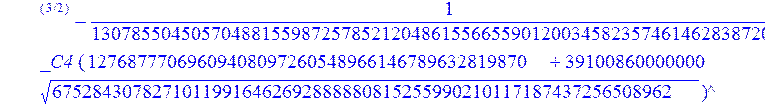
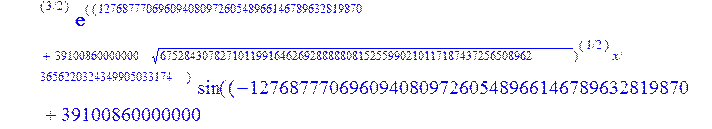
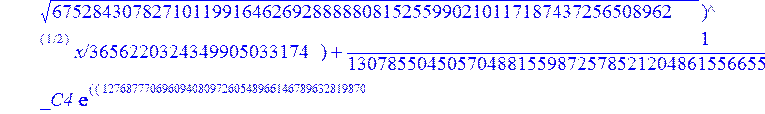
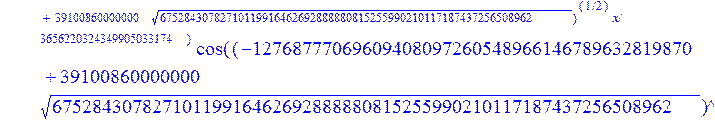
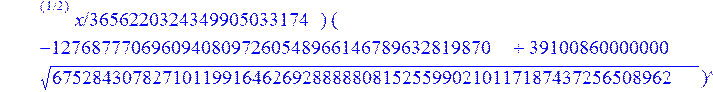
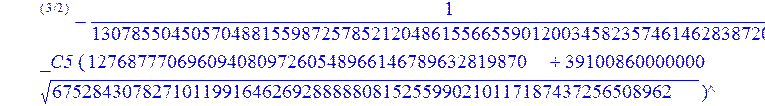
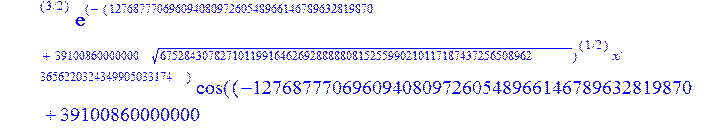
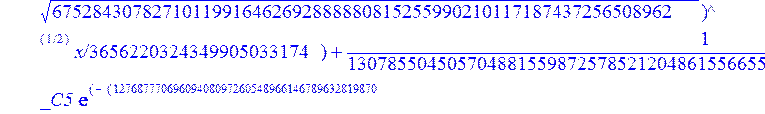
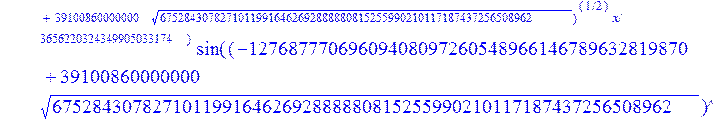
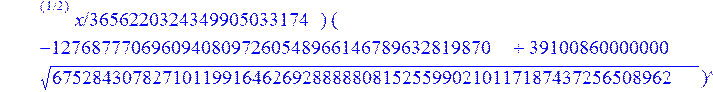
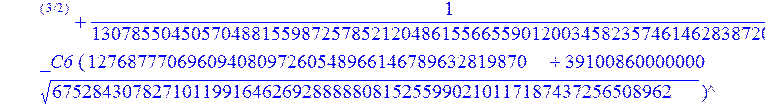
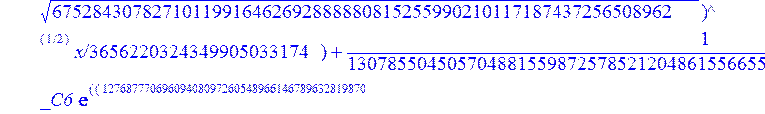
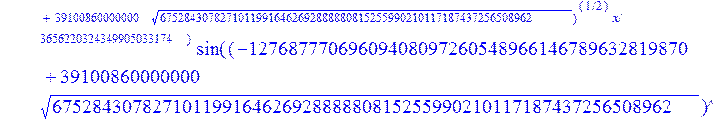
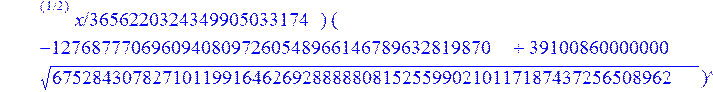
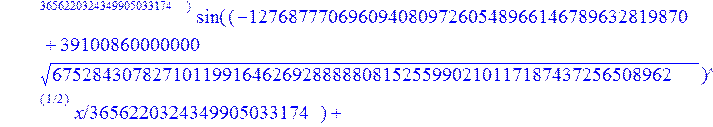
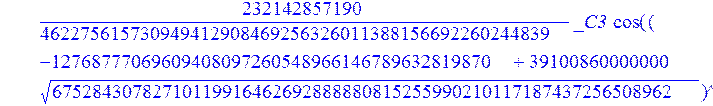
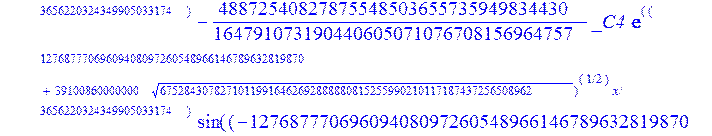
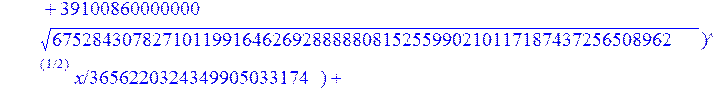
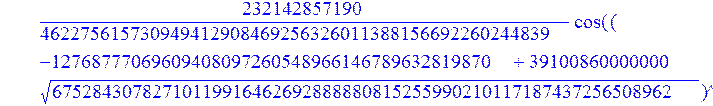
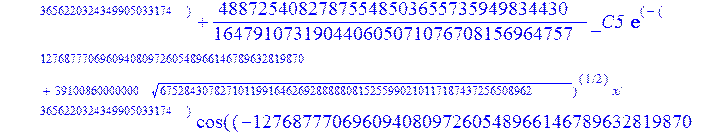
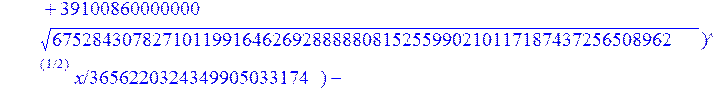
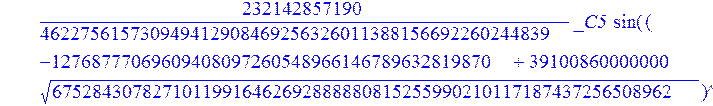
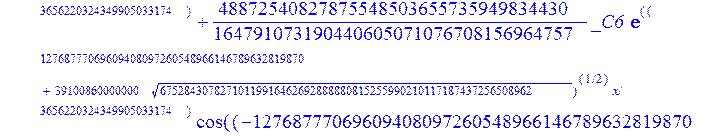
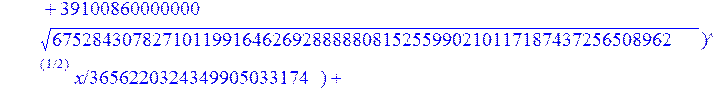
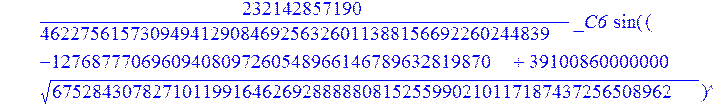
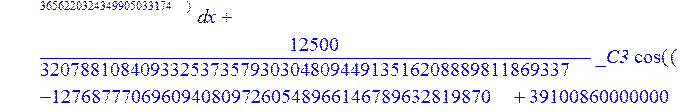
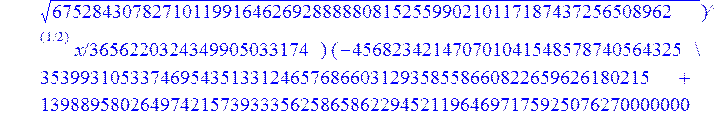
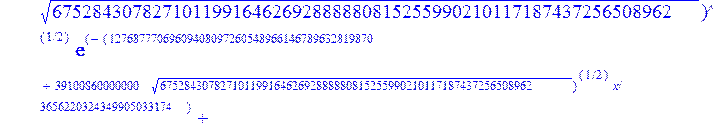
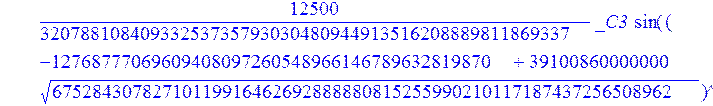
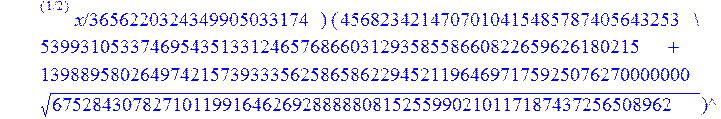
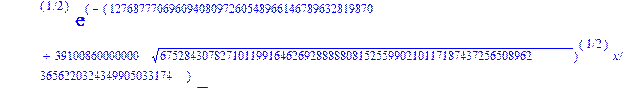
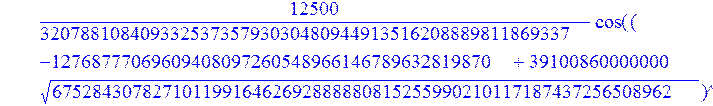
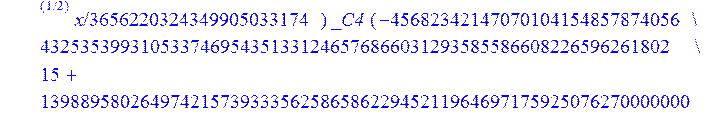
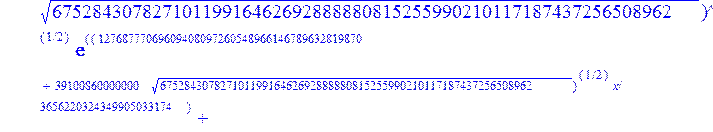
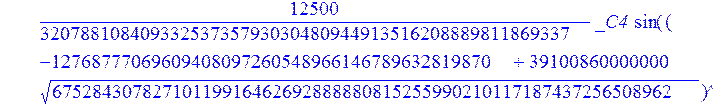
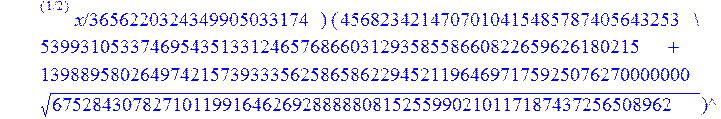
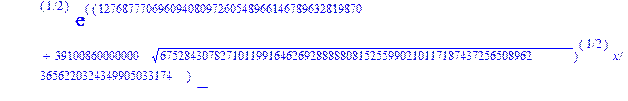
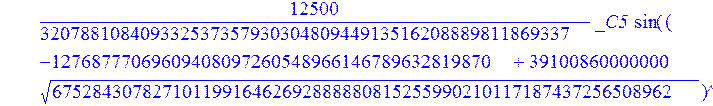
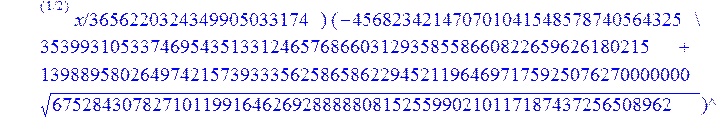
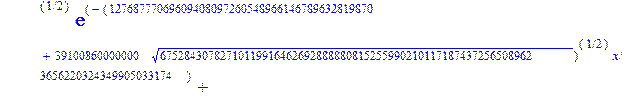
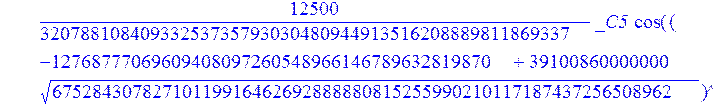
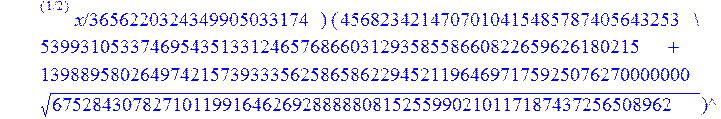
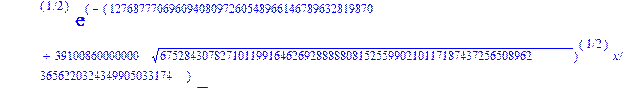
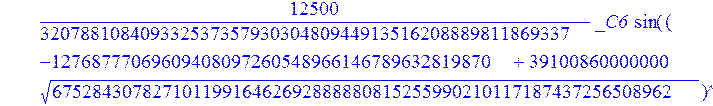
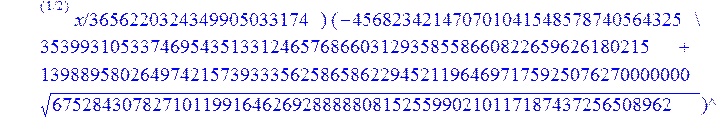
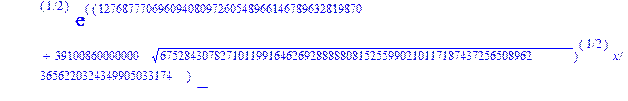
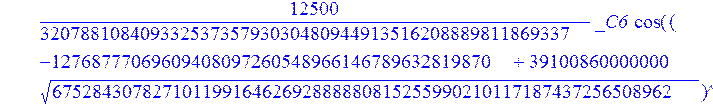
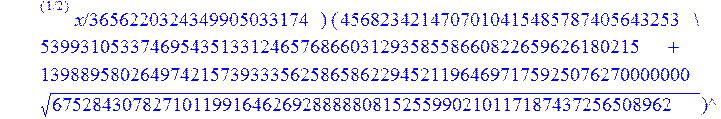
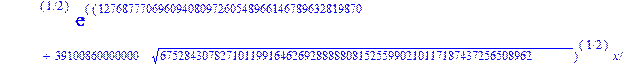
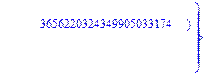
> restart:
> psi:=_C3*exp(-4.999132872*x)*sin(4.804266049*x)-1.*_C4*exp(4.999132872*x)*sin(4.804266049*x)+_C5*exp(-4.999132872*x)*cos(4.804266049*x)+_C6*exp(4.999132872*x)*cos(4.804266049*x); u:=.2965727444*_C3*(.2078556770e-1*exp(-4.999132872*x)*cos(4.804266049*x)+.826655854e-3*exp(-4.999132872*x)*sin(4.804266049*x))+.7422103084e-1*_C3*(.826655854e-3*exp(-4.999132872*x)*cos(4.804266049*x)-.2078556770e-1*exp(-4.999132872*x)*sin(4.804266049*x))-.2965727444*_C4*(-.2078556770e-1*exp(4.999132872*x)*cos(4.804266049*x)+.826655854e-3*exp(4.999132872*x)*sin(4.804266049*x))+.7422103084e-1*_C4*(.826655854e-3*exp(4.999132872*x)*cos(4.804266049*x)+.2078556770e-1*exp(4.999132872*x)*sin(4.804266049*x))+.2965727444*_C5*(.826655854e-3*exp(-4.999132872*x)*cos(4.804266049*x)-.2078556770e-1*exp(-4.999132872*x)*sin(4.804266049*x))-.7422103084e-1*_C5*(.2078556770e-1*exp(-4.999132872*x)*cos(4.804266049*x)+.826655854e-3*exp(-4.999132872*x)*sin(4.804266049*x))+.2965727444*_C6*(.826655854e-3*exp(4.999132872*x)*cos(4.804266049*x)+.2078556770e-1*exp(4.999132872*x)*sin(4.804266049*x))+.7422103084e-1*_C6*(-.2078556770e-1*exp(4.999132872*x)*cos(4.804266049*x)+.826655854e-3*exp(4.999132872*x)*sin(4.804266049*x))+_C1*x+_C2; w:=-.4500000000*_C1+.8142468344e-1*_C3*exp(-4.999132872*x)*sin(4.804266049*x)+.8142468346e-1*_C4*exp(4.999132872*x)*sin(4.804266049*x)+.8142468346e-1*_C5*exp(-4.999132872*x)*cos(4.804266049*x)-.8142468346e-1*_C6*exp(4.999132872*x)*cos(4.804266049*x)-.3339946388e-1*_C4*(.1039919598*exp(4.999132872*x)*cos(4.804266049*x)+.9993834021e-1*exp(4.999132872*x)*sin(4.804266049*x))+.9436859066e-1*_C3*exp(-4.999132872*x)*cos(4.804266049*x)-.9436859066e-1*_C4*exp(4.999132872*x)*cos(4.804266049*x)-.2559375000e-2-.9436859066e-1*_C5*exp(-4.999132872*x)*sin(4.804266049*x)-.9436859066e-1*_C6*exp(4.999132872*x)*sin(4.804266049*x)-.3339946388e-1*_C3*(-.1039919598*exp(-4.999132872*x)*cos(4.804266049*x)+.9993834021e-1*exp(-4.999132872*x)*sin(4.804266049*x))+.3339946388e-1*_C5*(-.9993834021e-1*exp(-4.999132872*x)*cos(4.804266049*x)-.1039919598*exp(-4.999132872*x)*sin(4.804266049*x))-.3339946388e-1*_C6*(-.9993834021e-1*exp(4.999132872*x)*cos(4.804266049*x)+.1039919598*exp(4.999132872*x)*sin(4.804266049*x))-.1334577350*_C3*(-.9993834021e-1*exp(-4.999132872*x)*cos(4.804266049*x)-.1039919598*exp(-4.999132872*x)*sin(4.804266049*x))+.1334577350*_C4*(-.9993834021e-1*exp(4.999132872*x)*cos(4.804266049*x)+.1039919598*exp(4.999132872*x)*sin(4.804266049*x))-.1334577350*_C5*(-.1039919598*exp(-4.999132872*x)*cos(4.804266049*x)+.9993834021e-1*exp(-4.999132872*x)*sin(4.804266049*x))-.1334577350*_C6*(.1039919598*exp(4.999132872*x)*cos(4.804266049*x)+.9993834021e-1*exp(4.999132872*x)*sin(4.804266049*x));
>
>
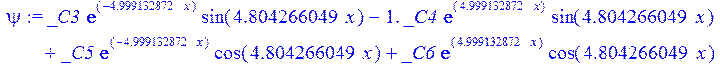
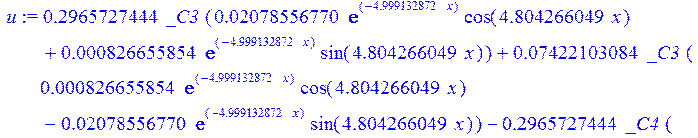
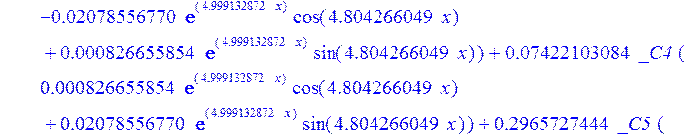
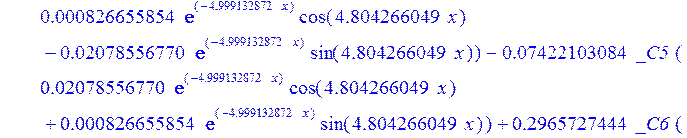
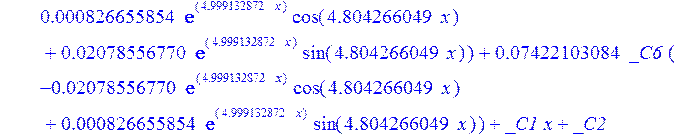
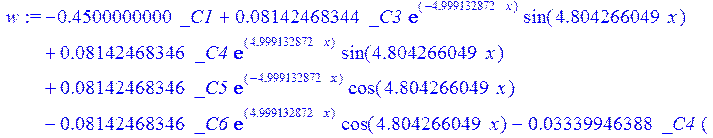
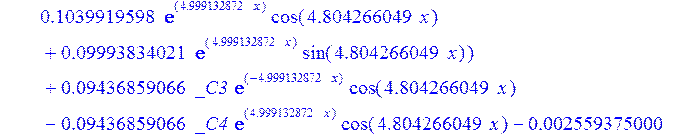
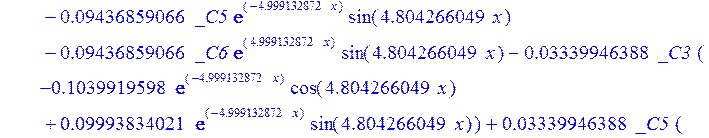
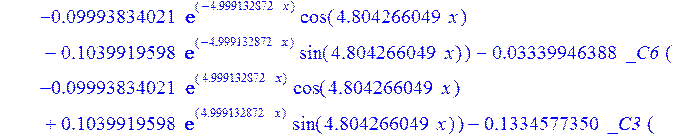
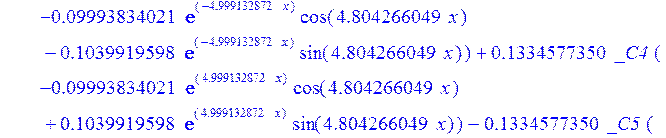
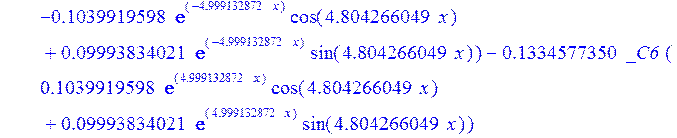
> h:=0.1; nu:=0.3; E:=1.6e11; P:=2e8; R:=0.45;l:=2;
> eq[1]:=eval(u,x=0)=0;
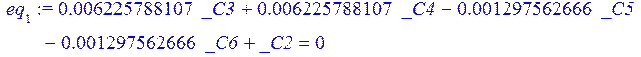
> eq[2]:=eval(u,x=l)=0;
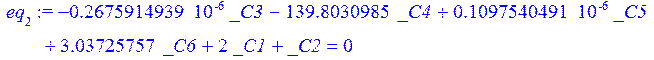
> eq[3]:=eval(psi,x=0)=0;
> eq[4]:=eval(w,x=0)=0;
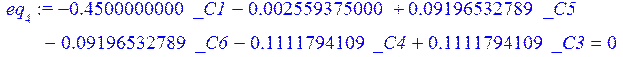
> eq[5]:=eval(w,x=l)=0;
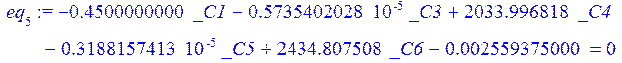
> eq[6]:=eval(diff(w,x),x=l/2)=0;
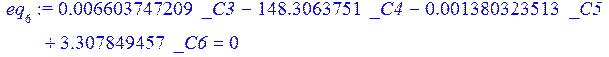
> sol:=solve({seq(eq[j],j=1..6)},{_C1,_C2,_C3,_C4,_C5,_C6});
>
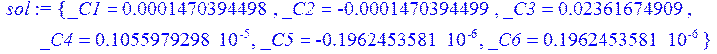
> U:=subs(sol,u); PSI:=subs(sol,psi); W:=subs(sol,w);
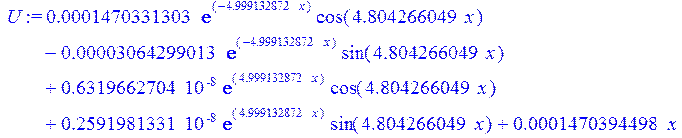
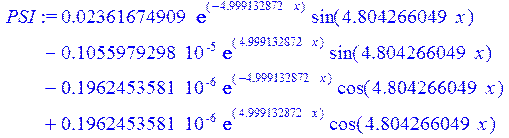
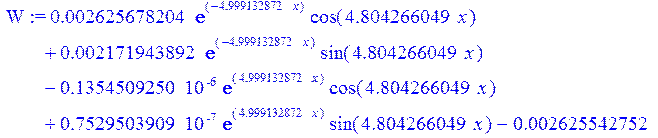
> simplify(eval(h^2*diff(PSI,x$2)+12*diff(U,x$2)+12*nu*W));
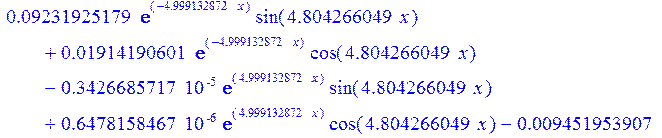
> simplify(eval(h^2/(6*(1-nu)*R)*(diff(U,x$2)+R*diff(PSI,x$2))-(PSI+diff(W,x))));
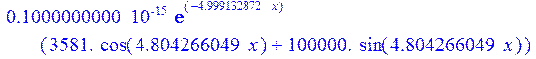
> simplify(eval(1/(2*(1+nu))*(diff(PSI,x)+diff
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
